티스토리 뷰
그리디 알고리즘은 탐욕 알고리즘, 욕심쟁이 알고리즘이라고도 불린다.
현재 상황에서 당장 눈앞에 보이는 최적의 결과를 선택해 나가는 방식이기 때문인데,
가장 간단한 예는 다음과 같다.
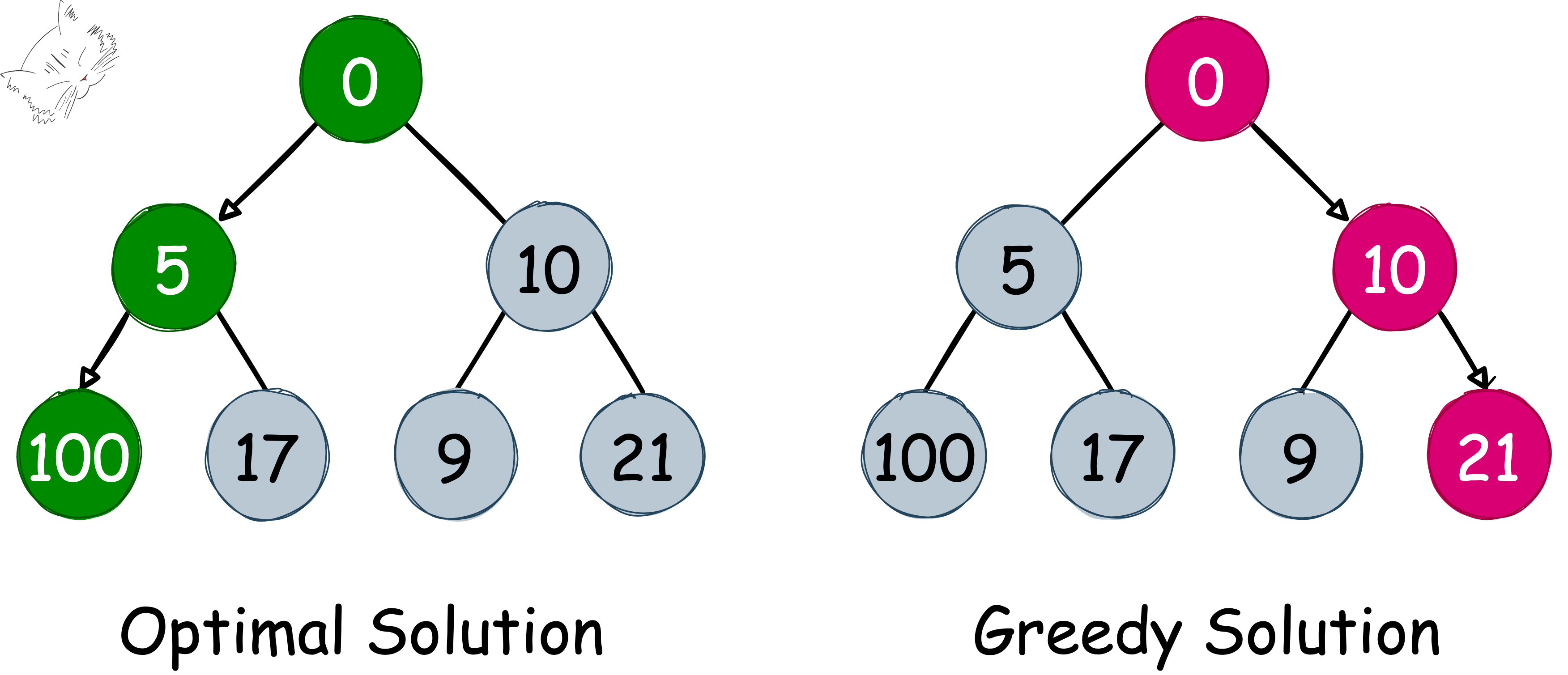
주어진 자료구조에서 가장 큰 합을 찾아내는 과정인데,
그리디 알고리즘은 그때그때 눈앞의 숫자 중 큰 쪽을 선택하는 것을 볼 수 있다.
구체적으로는 다음과 같이 단계를 셋으로 나눌 수 있다.
- 선택 절차(Selection Procedure): 현재 상태에서의 최적의 해답을 선택
- 적절성 검사(Feasibility Check): 선택된 해답이 문제의 조건을 만족하는지 검사
- 해답 검사(Solution Check): 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복
또한 위의 트리구조의 예에서 볼 수 있듯이, 그리디 알고리즘은 언제나 최적의 결과를 도출하지는 않는다.
그리디 알고리즘을 이용해 풀 수 있는 간단한 문제를 보자.
거스름돈 문제
당신은 음식점의 계산을 도와주는 점원이다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원 동전이 무한개 존재한다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러주어야 할 동전의 최소 개수를 구하라. (단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.)
위와 같은 문제가 주어졌을 때 우리는 큰 동전부터 개수를 채운다.
예를 들어 거슬러줘야 할 금액이 670원이라고 한다면,
500원짜리 한 개, 100원짜리 한 개, 50원짜리 한 개, 10원짜리 두 개를 선택할 것이다.
이를 그리디 알고리즘의 순서를 따라 풀면 아래와 같은 순서를 거친다.
- 선택 절차: 동전의 개수를 줄이기 위해 가장 큰 동전부터 선택
- 적절성 검사: 선택된 동전들이 답을 초과하는지 검사. 초과하면 마지막 동전 삭제 후 1번으로 돌아가 한 단계 작은 동전 선택
- 해답 검사: 선택된 동전들의 합이 거슬러줄 금액과 일치하는지 검사. 부족하면 1번부터 반복
그리디 알고리즘으로 얻어낸 답이 정답과 일치함을 확인할 수 있다.
함수 구현은 다음과 같다.
public static int coin(int money) {
int answer = 0;
int[] change = {500, 100, 50, 10};
for(int i = 0; i < change.length; i++) {
answer += money / change[i];
money = money % change[i];
}
return answer;
}쉬운 예시를 하나 더 보자.
분할 가능 가방 문제
🥖$3 / 40g | 🍞$1.5 / 25g | 🥯$2.5 / 5g | 🥐 $2 / 20g
장발장이 빵 가게에서 빵을 훔치려고 합니다. 장발장의 가방은 35g까지의 빵만 담을 수 있고, 빵은 가격이 전부 다르며, 4 개의 종류가 각 1 개씩 있습니다. 빵은 쪼개어 담을 수 있습니다. 장발장은 가방을 최대한 가격이 많이 나가는 빵으로 채우고 싶습니다.
위 문제를 그리디 알고리즘에 넣으면 다음과 같이 간단하게 풀 수 있다.
- 무게 대비 가장 비싼 빵을 넣는다.
- 다음으로 무게대비 비싼 빵을 넣는다.
- 만약 가방에 다 들어가지 않는다면 쪼개서 넣는다.
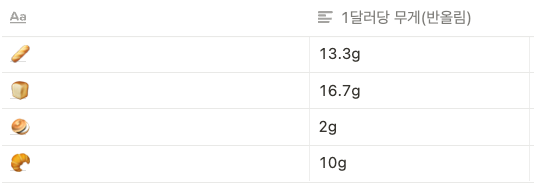
- $1당 2g인 🥯 3번 빵(5g) 먼저 가방에 담는다. 남은 가방의 무게: 30g
- $1당 10g인 🥐 4번 빵(20g)을 다음으로 담는다. 남은 가방의 무게: 10g
- $1당 13.3g인 🥖1번 빵(40g)을 다음으로 담는다
- 그러나, 40g을 온전히 못 채우기 때문에 쪼개어 10g만 넣는다: 남은 가방의 무게: 0g
위와 같은 식으로 총 $5.25 어치의 빵을 훔칠 수 있다는 답이 도출된다.
하지만 위의 문제에서 400원짜리 동전이 추가되거나, 빵을 쪼개지 못한다거나 하는 조건이 늘어나는 경우
그리디 알고리즘은 최적 해를 보장하지 못한다.
그리디 알고리즘이 적용되기 위해서는 문제가 다음의 두 조건을 만족시켜야 하는데,
- 탐욕적 선택 속성(Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않는다.
- 최적 부분 구조(Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
쉽게 말하면 지역적 최적 선택이 전체 문제의 해에 포함되며, 전체 문제의 해를 부분 문제로 구할 수 있다는 뜻이다.
'Algorithm > Algorithm' 카테고리의 다른 글
| [Java+Python]퀵 정렬(Quick Sort) (1) | 2022.12.26 |
|---|---|
| [Java+Python]힙 정렬(Heap Sort) (2) | 2022.12.21 |
| [Java+Python]병합 정렬(Merge Sort) (3) | 2022.12.20 |
| [Java+Python]선택 정렬(Selection Sort) (4) | 2022.12.19 |
| [Java+Python]버블 정렬(Bubble Sort) (3) | 2022.12.18 |
| [Java+Python]삽입 정렬(Insert Sort) (1) | 2022.12.17 |
- Total
- Today
- Yesterday
- spring
- 스프링
- 알고리즘
- 리스트
- 칼이사
- 맛집
- 유럽
- 지지
- 여행
- RX100M5
- 세모
- Algorithm
- BOJ
- 스트림
- a6000
- 남미
- Backjoon
- 백준
- java
- 세계여행
- 파이썬
- 야경
- 유럽여행
- 중남미
- 세계일주
- 면접 준비
- 기술면접
- 동적계획법
- Python
- 자바
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
