티스토리 뷰
<Java + Python>으로 구현한 다른 정렬:
[Java+Python]삽입 정렬(Insert Sort)
[Java+Python]버블 정렬(Bubble Sort)
병합 정렬은 전설적인 수학자 폰 노이만이 고안한 알고리즘으로,
대상을 모두 쪼갠 뒤 다시 합치며(Merge) 크기를 비교해 정렬하는 방식이다.
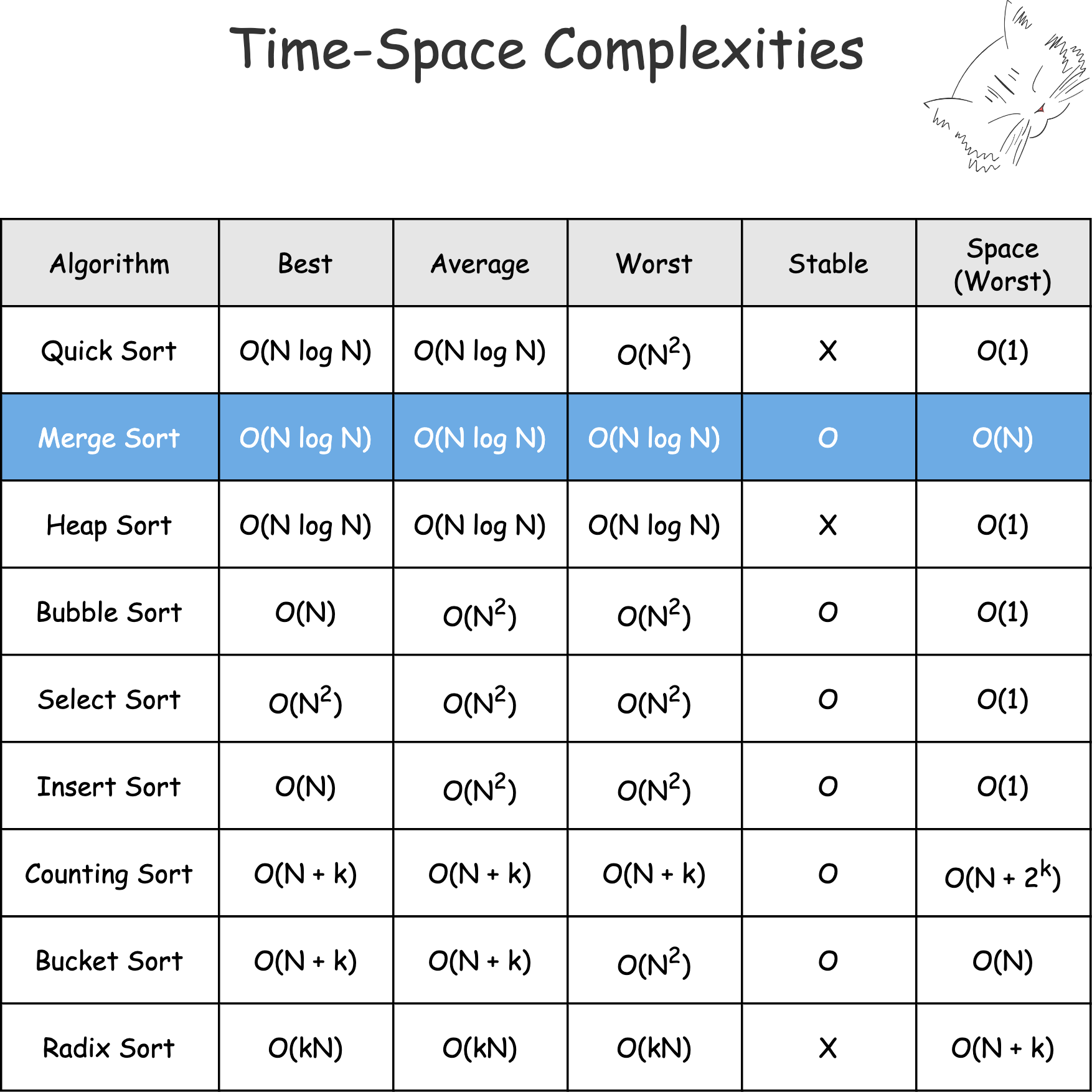
앞서 알아본 버블, 선택, 삽입 정렬에 비해 빠르나 퀵 정렬에 비해 성능이 떨어지고,
정렬 대상의 크기만 한 메모리를 요구하지만 힙, 퀵 정렬과는 다르게 안정적인 정렬이라는 특징이 있다.
추가로 병합 정렬과 힙 정렬은 자료의 상태에 영향을 받지 않고 항상 일정한 시간 복잡도를 보인다.
또한 정렬이 끝난 두 배열을 합칠 땐 병합 정렬의 마지막 단계를 이용하는 것이 가장 빠르다고 한다.
계속해서 작동 방식과 구현에 대해 살펴보자.
Algorithm
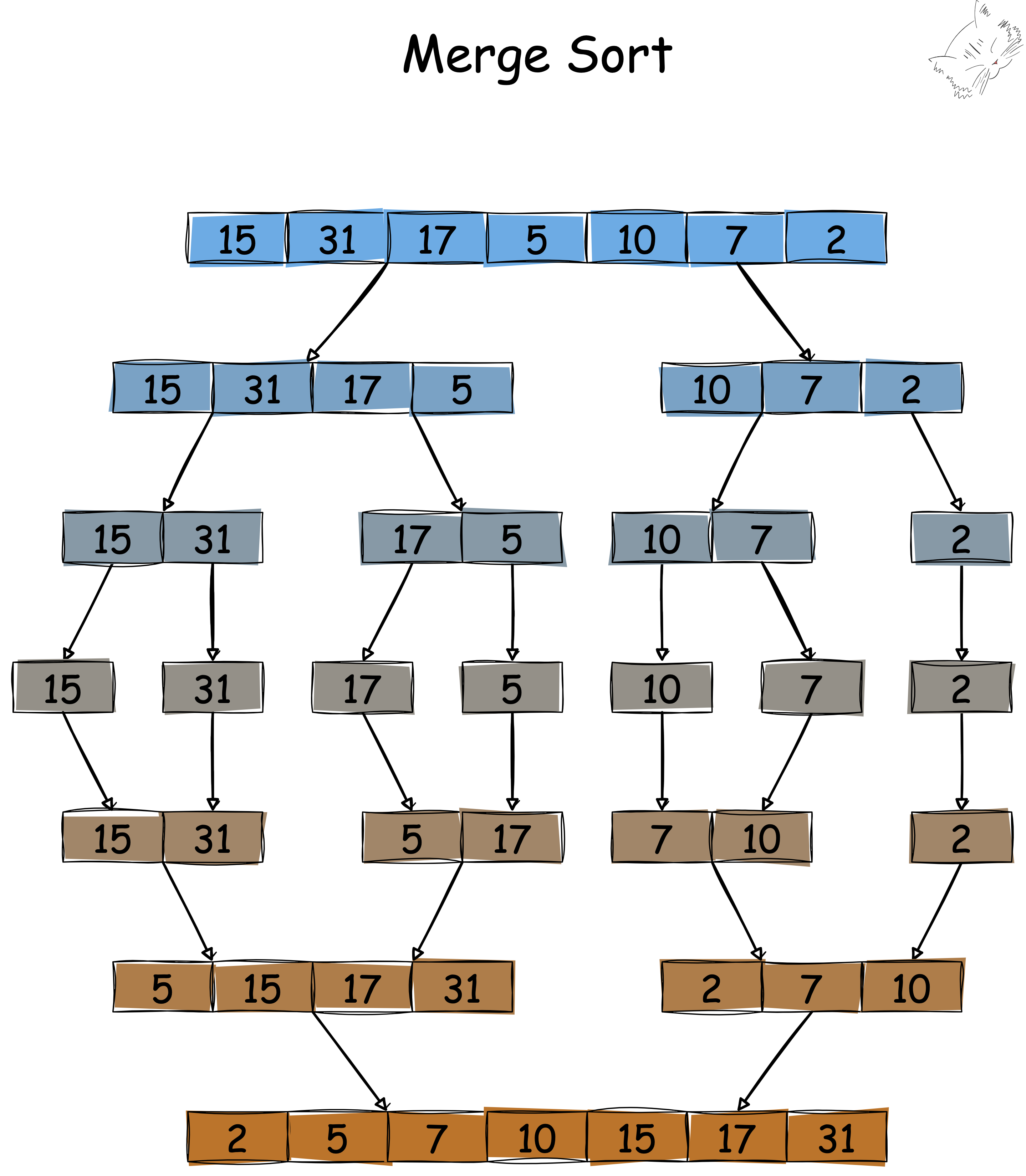
그림으로 보면 세상 직관적인 알고리즘이다.
더이상 쪼갤 수 없을 때까지 쪼갠 후 합치며 정렬하는 방식은 어디서 많이 듣던 방법이다.
추가로 위에 언급했듯이 만일 원소의 크기가 같다면 정렬하지 않고 기존 순서를 유지한다.
Implementation
최소 단위까지 자른 후 다시 합친다.
재귀 함수를 다룰 때 많이 듣던 개념이다.
예상대로 병합 정렬의 구현은 재귀 호출을 사용하는 것이 가장 편하다.
주의할 점은 합치기 시작하고 나선 각 조각은 내부적으로는 정렬이 끝나 있다는 사실이다.
합치기 전 조각의 원소들 끼리는 비교할 필요가 없다는 뜻이다.
import java.util.Arrays;
public class MergeSort {
private static int[] temp; // 임시 배열 전역변수로 선언
public static void main(String[] args) {
int[] arr = {4, 16, 31, 5, 4, 17, 1, 10, 15, 3, 16, 6, 7, 2, 2, 1, 5, 13, 17, 14, 4, 0};
temp = new int[arr.length];
mergeSortImpl(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void mergeSortImpl(int[] arr, int start, int end) {
if (start == end) return; // 끝까지 쪼개면 리턴
int mid = (start + end) / 2; // 절반으로 나누기
mergeSortImpl(arr, start, mid); // 왼쪽 절반 재귀호출
mergeSortImpl(arr, mid + 1, end); // 오른쪽 절반 재귀호출
// -----------------------------------------------------------
// 쪼개기 끝났으니 합치기
// -----------------------------------------------------------
int left = start; // 왼쪽 부분 배열 시작점
int right = mid + 1; // 오른쪽 부분 배열 시작점
int idx = left; // 비교 후 채워넣을 배열의 인덱스
while (left <= mid && right <= end) {
/*
* 왼쪽 부분 배열의 left 번째 요소가 오른쪽 부분 배열의 right 번째 요소보다 작거나 같을 경우
* idx 자리에 left 번째 요소를 넣고 left++ && idx++
*/
if (arr[left] <= arr[right]) {
temp[idx] = arr[left];
idx++;
left++;
}
/*
* 반대의 경우
*/
else {
temp[idx] = arr[right];
idx++;
right++;
}
}
/*
* 왼쪽 부분 배열이 먼저 전부 비워졌을 경우(left > mid)
* 오른쪽 부분 배열은 아직 남아있으므로
* 순서대로 나머지 원소를 채워넣는다
*/
if (left > mid) {
while (right <= end) {
temp[idx] = arr[right];
idx++;
right++;
}
}
/*
* 반대의 경우
*/
else {
while (left <= mid) {
temp[idx] = arr[left];
idx++;
left++;
}
}
/*
* 기존 배열에 넣어주기
*/
for (int i = start; i <= end; i++) {
arr[i] = temp[i];
}
}
}[0, 1, 1, 2, 2, 3, 4, 4, 4, 5, 5, 6, 7, 10, 13, 14, 15, 16, 16, 17, 17, 31]계속해서 파이썬 코드이다.
list = [4, 16, 31, 5, 4, 17, 1, 10, 15, 3, 16, 6, 7, 2, 2, 1, 5, 13, 17, 14, 4, 0] # 정렬 대상
temp = [0] * len(list) # 정렬된 값을 담을 임시 배열. 대상의 크기와 동일하게 생성 및 0으로 초기와 해준다.
def merge_sort(list, start, end):
if start == end:
return # 최소단위까지 쪼개면 리턴
mid = (start + end) // 2 # 주어진 요소의 중간 값을 찾는다
merge_sort(list, start, mid) # 왼쪽 절반에 대해 재귀호출
merge_sort(list, mid + 1, end) # 오른쪽 절반에 대해 재귀호출. 왼쪽 절반이 모두 끝난 뒤에 호출된다.
########################
# 쪼개기 끝났으니 합치기 시작 #
########################
left = start # 왼쪽 조각의 시작점
right = mid + 1 # 오른쪽 조각의 시작점
idx = left # 비교후 temp에 채워넣을 인덱스
while left <= mid and right <= end:
###########################################################
# 왼쪽 조각의 left번째 요소가 오른쪽 조각의 right번째 요소보다 작을 경우 #
# temp의 idx에 left번째 요소를 삽입한 뒤 left와 idx += 1 #
###########################################################
if list[left] <= list[right]:
temp[idx] = list[left]
idx += 1
left += 1
# 반대의 경우 right번째 요소로 동일한 작업 수행
else:
temp[idx] = list[right]
idx += 1
right += 1
###########################################################
# 왼쪽 조각의 요소가 먼저 떨어졌을 경우(left > mid) #
# 오른쪽 조각은 아직 남아있기 때문에 순서대로 나머지를 채워넣는다. #
# 비교하지 않고 채워넣는 이유는 모든 조각은 이미 정렬이 끝난 상태이기 때문! #
###########################################################
if left > mid:
while right <= end:
temp[idx] = list[right]
idx += 1
right += 1
# 반대의 경우
else:
while left <= mid:
temp[idx] = list[left]
idx += 1
left += 1
# 병합이 모두 끝나면 temp를 리스트에 넣어준다.
for i in range(start, end + 1):
list[i] = temp[i]
merge_sort(list, 0, len(list) - 1)
print(list)[0, 1, 1, 2, 2, 3, 4, 4, 4, 5, 5, 6, 7, 10, 13, 14, 15, 16, 16, 17, 17, 31]코드가 길어 보이지만 위에 그림으로 그려놓은 것을 그대로 옮겨둔 것에 불과하다.
재귀는 사용할 때마다 헷갈려서 주석을 많이 달게 된다.
'Algorithm > Algorithm' 카테고리의 다른 글
| [Java+Python]카운팅 정렬(Counting Sort) (4) | 2022.12.27 |
|---|---|
| [Java+Python]퀵 정렬(Quick Sort) (1) | 2022.12.26 |
| [Java+Python]힙 정렬(Heap Sort) (2) | 2022.12.21 |
| [Java+Python]선택 정렬(Selection Sort) (4) | 2022.12.19 |
| [Java+Python]버블 정렬(Bubble Sort) (3) | 2022.12.18 |
| [Java+Python]삽입 정렬(Insert Sort) (1) | 2022.12.17 |
- Total
- Today
- Yesterday
- spring
- 리스트
- a6000
- Python
- BOJ
- 남미
- java
- 기술면접
- 세계일주
- RX100M5
- 백준
- 칼이사
- 파이썬
- 세모
- 중남미
- 자바
- 스트림
- 야경
- 스프링
- 맛집
- Algorithm
- 여행
- 유럽여행
- 동적계획법
- 세계여행
- 알고리즘
- 면접 준비
- Backjoon
- 유럽
- 지지
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
