티스토리 뷰
728x90
반응형
자료구조에서의 그래프는 굉장히 일반적인 개념이고 그 예가 많지만,
특정 기준을 이용해 둘로 나누면 아래와 같이 구분할 수 있다.

바로 무방향 그래프(G1)와 방향 그래프(G2)인데,
이와 같은 자료구조를 자바에 구현하는 방법은 크게 두 가지가 존재한다.
하나씩 알아보자.
Adjacency Matrix
인접 행렬은 말 그대로 노드간의 관계를 행렬로 나타낸 것이다.
노드가 n개인 그래프의 인접행렬은 n X n 정사각 행렬이 되며, 인접한 경우엔 1, 그렇지 않은 경우엔 0을 채워 넣는다.

추가로 무방향 그래프의 경우엔 인접 행렬이 대칭을 이루고 있는 것이 특징이다.
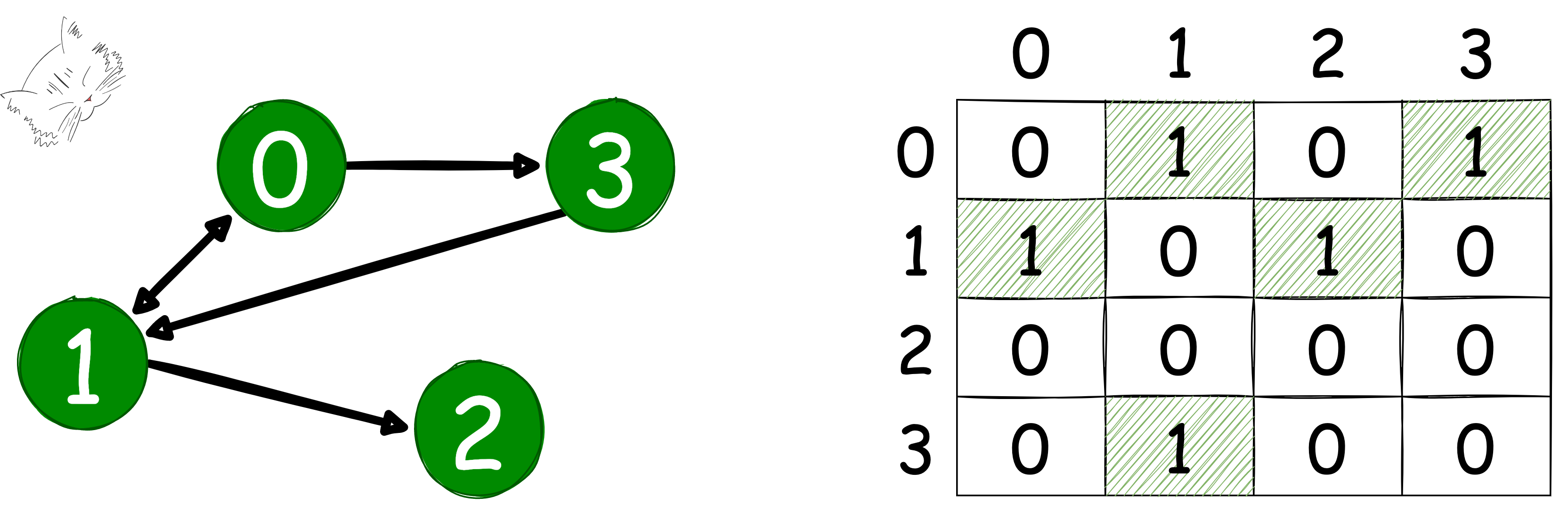
방향 그래프의 경우엔 반드시 대칭 행렬을 이루지는 않는다.
인접 행렬의 장점은 노드 사이의 빠른 경로를 찾기 편하다는 점이며
단점은 간선의 유무와 상관없이 노드 개수에 따라 메모리 공간을 차지해 낭비가 발생할 수 있다는 점이다.
Adjacency List
인접 리스트는 노드 간의 관계를 리스트로 만들어 정리한다.
노드 개수만큼 리스트를 생성한 뒤 인접 노드를 원소로 추가하는 식으로 처리된다.
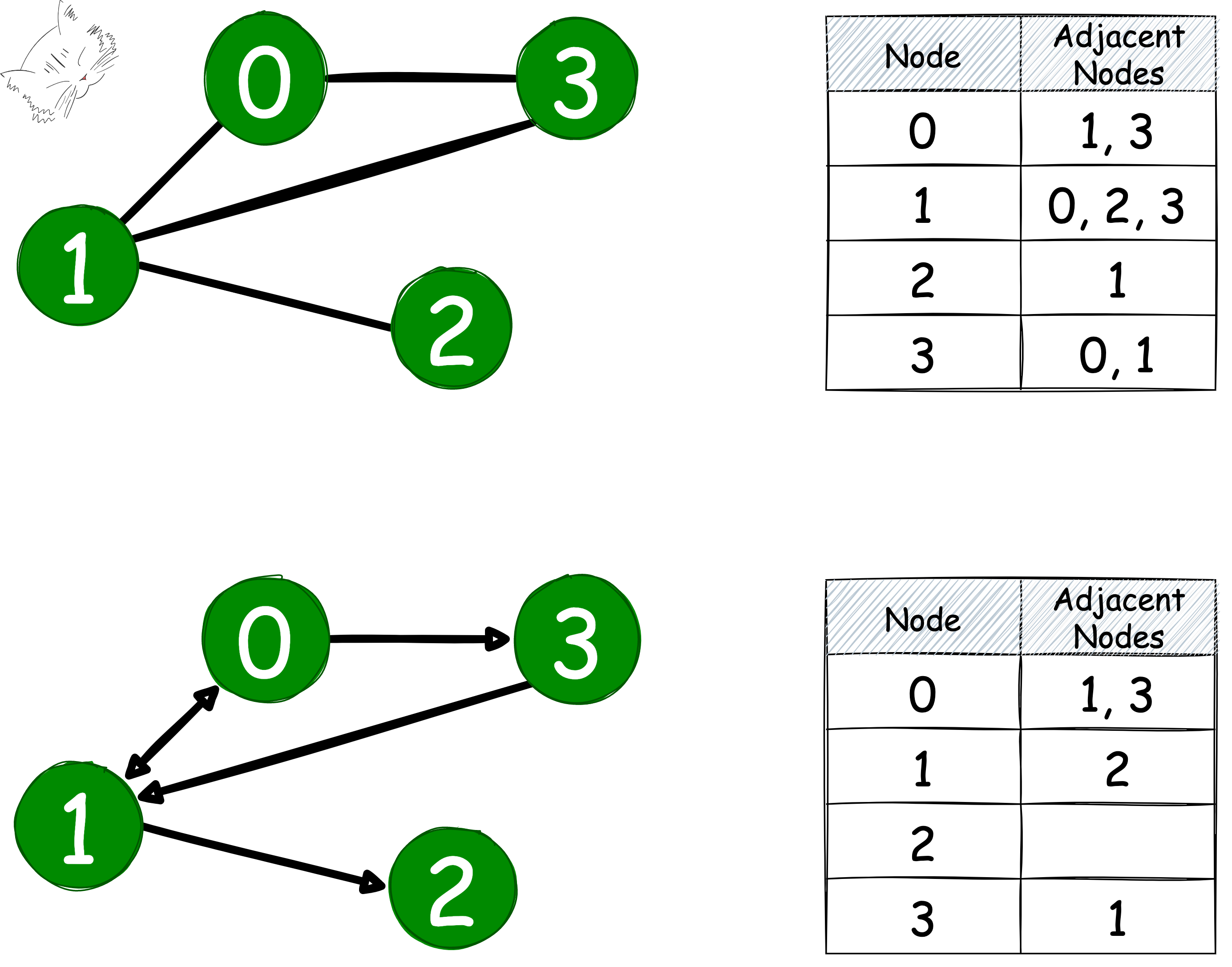
인접 행렬과 다르게 메모리를 효율적으로 사용할 수 있다는 장점이 있지만
노드간의 연결 여부 확인을 위해 모든 노드를 탐색해야 해서 속도가 느리다는 단점이 있다.
Summary
| 인접 행렬(노드 개수 N) | 인접 리스트(노드 개수 N) | |
| 방식 | NXN 정사각 행렬을 만들어 0, 1로 관계 표시 | N개의 리스트를 만들어 인접 노드를 원소로 추가 |
| 장점 | 노드 간의 연결 정보를 빠르게 얻을 수 있다. 구현이 상대적으로 쉽다. 간선이 많은 경우 유리하다. |
메모리를 적게 차지한다. 모든 노드를 방문해야 할 때 효율적이다. 특정 노드의 인접 노드를 빠르게 알 수 있다. 간선이 적은 경우 유리하다. |
| 단점 | 연결정보와 관계없이 메모리를 차지해 낭비 가능성이 있다. 특정 노드를 방문하려 할 때 전부 확인해야 해 비효율적이다. |
노드간의 연결정보를 확인하려면 모든 노드를 탐색해야 한다. |
반응형
'Development > Technical Interview' 카테고리의 다른 글
| [면접 준비 - CS]Garbage Collection, G1GC, 그리고 (3) | 2022.12.15 |
|---|---|
| [면접 준비 - Algorithm]재귀 함수 vs. 반복문 (2) | 2022.12.14 |
| [면접 준비 - Algorithm]재귀, 재귀 함수 (0) | 2022.12.14 |
| [면접 준비 - Algorithm]이진 트리 순회, 이진 탐색 트리(BST), 힙 트리 (2) | 2022.12.14 |
| [면접 준비 - Algorithm]Stack, Queue, Tree, Graph (1) | 2022.12.14 |
| [면접 준비 - Java]제네릭(Generic)에 대하여 (4) | 2022.12.14 |
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 리스트
- 기술면접
- 세계여행
- 동적계획법
- 스트림
- 파이썬
- 남미
- Python
- java
- BOJ
- Backjoon
- 백준
- 칼이사
- RX100M5
- 여행
- a6000
- 면접 준비
- 스프링
- 세모
- spring
- 맛집
- 자바
- Algorithm
- 유럽
- 유럽여행
- 야경
- 알고리즘
- 세계일주
- 지지
- 중남미
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
글 보관함
