티스토리 뷰
Java+Python으로 더 간결하게 순열/조합/중복순열/중복조합 구현하기
[Java+Python]15649번, N과 M(1), 순열
[Java+Python]15650번, N과 M(2), 조합
순열(Permutation)
순열은 서로 다른 n개의 원소에서 r개를 중복 없이, 순서에 상관있게 뽑아 나열하는 것이다.
nPr의 형태로 자주 표현되며, 그 경우의 수는 아래와 같다.

순열을 탐색할 땐 재귀 함수로 표현하는 것이 편한데, 이 경우 해당 인덱스의 숫자가 사용 중인지 판단하는 배열이 따로 필요하다.
이미 뽑은 숫자라면 넘어가야 하기 때문이다.
import java.util.Arrays;
public class BruteForce4 {
public static void main(String[] args) {
n = 5;
numbers = new int[n];
isSelected = new boolean[n+1];
Permutation(0);
System.out.println("순열의 개수: " + count);
}
static int n; // 원소 개수
static int[] numbers; // 순열을 저장할 배열
static boolean[] isSelected; // 뽑았는지 여부를 저장할 배열
static int count; // 순열 개수
public static void Permutation(int k) {
// base condition
if(k == n) {
count++;
System.out.println(Arrays.toString(numbers));
return;
}
for(int i = 1; i <= n; i++) {
if (isSelected[i]) continue; // 중복 검사
// 중복이 아니라면
numbers[k] = i;
isSelected[i] = true;
Permutation(k + 1); // 다음 요소 뽑기
isSelected[i] = false;
}
}
}1부터 n까지의 숫자로 순열을 만드는 코드이다.
주어진 n개의 배열 중 r개를 뽑는 코드는 어떻게 작성해야 할까?

출처: https://minhamina.tistory.com/37?category=837168
[Java] 순열 Permutation
순열 순열이란 n 개의 값 중에서 r 개의 숫자를 모든 순서대로 뽑는 경우를 말한다. 수학에서 순열은 서로 다른 n개의 원소에서 r개를 뽑아한 줄로 세우는 경우의 수이다. 순열의 개수는 n의 계
minhamina.tistory.com
DFS를 이용해 모든 노드를 방문하며 순열을 만들어낼 수 있다.
이미 사용된 값은 isVisited를 true로 바꿔 재사용을 막는다.
depth는 여태까지 뽑은 순열의 길이이며, r과 같아질 경우 output을 출력한다.
public class Permutation {
public static void main(String[] args) {
int[] arr = {1, 2, 3}; // 순열을 만들 배열
int n = arr.length; // 배열의 길이
int[] output = new int[n]; // 순열을 저장하기 위한 배열
boolean[] isVisited = new boolean[n]; // 선택했는지 체크하는 배열
per(arr, output, isVisited, 0, n, 2); // 2개를 뽑는 경우(r = 2)
}
//순서를 지키면서 n 개중에서 r 개를 뽑는 경우
static void per(int[] arr, int[] output, boolean[] isVisited, int depth, int n, int r) {
if (depth == r) { // base condition
print(output, r); //순열 출력을 위한 print 함수
return;
}
for(int i = 0; i < n; i++) {
if (isVisited[i] != true) {
isVisited[i] = true;
output[depth] = arr[i];
per(arr, output, isVisited, depth + 1, n, r); // 재귀함수 호출
isVisited[i] = false;
}
}
}
static void print(int[] arr, int r) { // 배열 출력을 위한 메서드
for(int i = 0; i < r; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}{1, 2, 3} 배열을 이용해 2개를 순서에 상관있게 뽑아 나열하는 코드이다.
// 출력 결과
1 2
1 3
2 1
2 3
3 1
3 2
조합(Combination)
조합은 서로 다른 n개의 원소에서 r개를 중복 없이, 순서에 상관없이 뽑아 나열하는 것이다.
순열에선 {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}이 전부 다른 경우의 수였지만
조합에선 {1, 2, 3} 하나의 경우의 수로 센다는 뜻이다.
그러니까 순열의 경우의 수 nPr을 r!로 나눠주면 조합의 경우의 수가 된다.

조합에는 또 한 가지 재미있는 특성이 있는데, nCr = n-1Cr-1 + n-1Cr로 쪼갤 수 있다는 점이다.
증명은 아래와 같다.

말로 풀어서 설명하면 nCr은 원소중 하나를 골라 반드시 선택할 경우의 수와 반드시 선택하지 않을 경우의 수를 더한 것과 같다.
{1, 2, 3}배열에서 2개를 뽑는 경우의 수, 그러니까 3C2의 경우를 생각해보자.
- 1을 반드시 선택할 경우의 수 -> {1, 2}, {1, 3} = 2C1
- 1을 반드시 선택하지 않을 경우의 수 -> {2, 3} = 2C2
모든 경우의 수는 3C2 = 2C1 + 2C2 = 3인 것을 알 수 있다.
계속해서 2C1은 1C1 + 1C0으로 쪼갤 수 있으며, 더 이상 쪼개지지 않을 때까지 쪼갠 수 그 숫자를 더해주면 된다.
이를 기초로 먼저 nCr의 값을 구하는 코드를 작성해 보자.
public class Combination {
public static void main(String[] args) {
System.out.println(combination(3, 2)); // nCr의 값
}
static int combination(int n, int r) {
if(n == r || r == 0) // base condition
return 1;
else
return combination(n - 1, r) + combination(n - 1, r - 1); // 재귀 함수 호출
}
}n == r이 되거나 r == 0이 될 때까지 조합을 쪼개서 계산해준 것을 알 수 있다.
계속해서 nCr의 모든 경우의 수를 출력하는 코드를 작성해 보자.
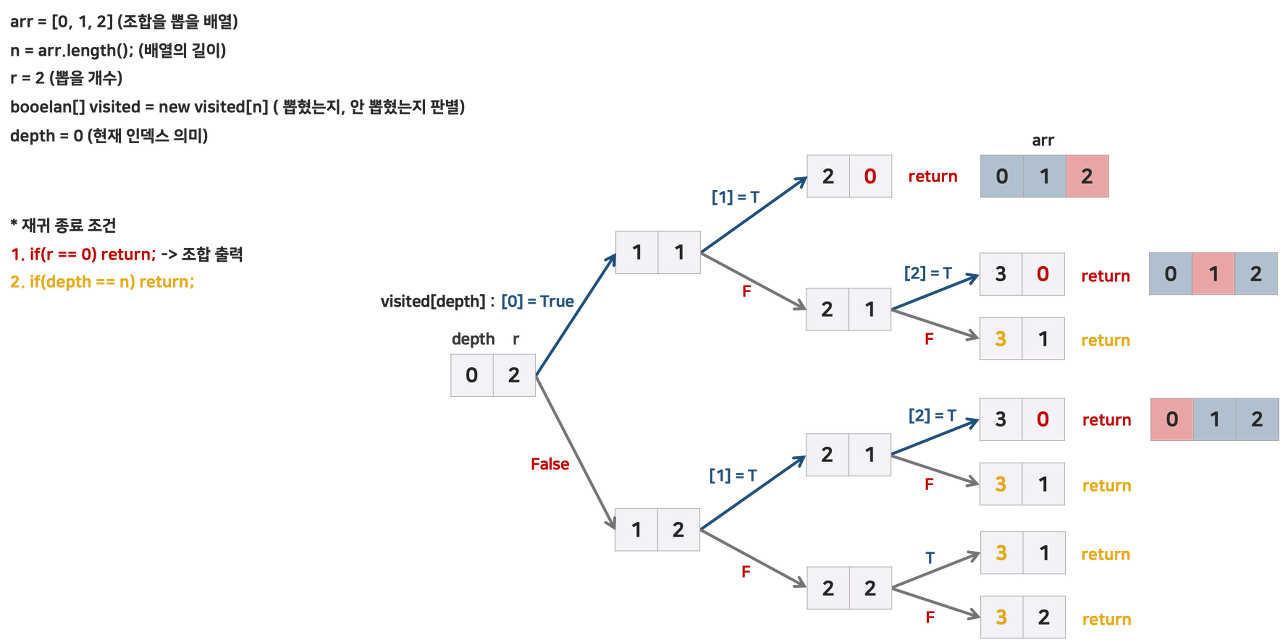
순열의 경우와 비슷하게 depth는 여태까지 뽑은 순열의 길이이며, 0부터 시작한다.
원소 하나를 반드시 선택한 경우와 선택하지 않은 경우로 나누어서 모두 살펴봐야 하고,
이미 고른 숫자는 더이상 보지 않으므로 depth는 1씩 증가한다.
r == 0이 되면 조합이 완성되었다는 뜻이므로 선택했던 숫자를 출력하고,
그 이전에 n == r이 된다면 조합을 만들 수 없다는 뜻이므로 재귀를 종료한다.
출처: https://minhamina.tistory.com/38
[Java] 조합 Combination
조합 조합이란 n 개의 숫자 중에서 r 개의 수를 순서 없이 뽑는 경우를 말한다. (위키백과 - 수학에서 조합은 서로 다른 n개의 원소 중에서 순서에 상관없이 r개를 선택하는 것이다. 그 경우의
minhamina.tistory.com
public class Combination {
public static void main(String[] args) {
int[] arr = {1, 2, 3}; //조합을 만들 배열
int n = arr.length;
int r = 2;
boolean[] isVisited = new boolean[arr.length];
comb(arr, isVisited, 0, n, r); // nCr 경우의 수 출력
}
static void comb(int[] arr, boolean[] isVisited, int depth, int n, int r) {
if(r == 0) { // base condition
print(arr, isVisited);
return;
}
if(depth == n) {
return;
} else {
isVisited[depth] = true;
comb(arr, isVisited, depth + 1, n, r - 1); // 재귀함수 호출
isVisited[depth] = false;
comb(arr, isVisited, depth + 1, n, r);
}
}
static void print(int[] arr, boolean[] isVisited) { // 배열 출력을 위한 메서드
for(int i = 0; i < arr.length; i++) {
if(isVisited[i] == true)
System.out.print(arr[i] + " ");
}
System.out.println();
}
}{1, 2, 3} 배열을 이용해 순서에 상관없이 2개를 뽑는 코드이다.
// 출력 결과
1 2
1 3
2 3
'Algorithm > DFS' 카테고리의 다른 글
| [Java+Python]15651번, N과 M(3), 중복순열 (0) | 2023.05.02 |
|---|---|
| [Java+Python]15650번, N과 M(2), 조합 (0) | 2023.04.28 |
| [Java+Python]15649번, N과 M(1), 순열 (0) | 2023.04.27 |
| [Java]중복 조합(Combination with Repetition) (0) | 2022.08.01 |
| [Java]중복 순열(Permutation with repetition), 가위 바위 보 문제 (0) | 2022.08.01 |
| [Java]BFS / DFS (0) | 2022.07.27 |
- Total
- Today
- Yesterday
- 스프링
- 백준
- 칼이사
- 알고리즘
- 기술면접
- spring
- 세모
- 여행
- Algorithm
- 면접 준비
- 지지
- BOJ
- 야경
- 자바
- 유럽
- a6000
- 동적계획법
- 파이썬
- 남미
- RX100M5
- 세계일주
- 맛집
- 중남미
- 리스트
- 유럽여행
- Backjoon
- 스트림
- java
- 세계여행
- Python
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
