티스토리 뷰
목차
DB 설계에서 시작해 제법 멀리도 왔다. 시작점이 안 보여.
어쨌거나 DB는 한 번 잘못 설계하면 그 알아채는 타이밍이 늦을수록 돈이 들어간다.
게다가 만약 그 설계가 데이터 무결성을 무너뜨리는 것을 모자라 데이터 보안까지 위협한다?
돈으로 해결되면 다행일 것이다.
반면 당연하게도 안정적이고 성능 좋은 DB를 설계한다면 여러 비용을 절약할 수 있다.
DB 설계의 세 번째 단계인 논리적 설계에서 시작해 데이터 무결성과 그 제약조건을 거쳐 여기까지 왔다.
이 글에선 DB 설계 시 개발자가 기본적으로 알아야 할, 효율적인 디자인에 대해 다룬다.
그럼 여기서 먼저, DB의 효율성이란 무엇일까? 당연히 삽입/갱신/삭제/조회의 비용이 적은 것을 말한다.
그럼 이어서, DB의 효율성을 가장 많이 해치는 근본적인 문제는 무엇일까? 바로 데이터의 중복이다.
데이터의 중복이 많을수록 CRUD시 DB가 이상(Anomaly)을 일으킬 확률이 높아진다.
따라서 앞으로 살펴볼 스키마 정제와 DB 정규화의 목적은 바로 이 데이터 중복을 최대한 제거하는 것이 목적이다.
그 방법은 주로 테이블을 작게 쪼개는 것으로 나타나며,
당연히 아무 때나 아무렇게나 테이블을 쪼갤 수는 없기 때문에 원칙과 근거에 따라 문제 가능성이 없는 경우를 골라
신중하게 쪼개야 한다.
Functional Dependency
함수형 종속은 정규화의 밑바탕이 되는 기준이다.
테이블을 쪼개기 전에 먼저 종속 유형을 파악하고 그에 따라 정규화의 방식을 결정한다.
한 테이블의 컬럼 X, Y에 대해 함수형 종속은 다음과 같이 표시하며,
$$X → Y$$
이는 테이블에서 X의 값에 대응하는 Y가 유일하다는 뜻이다.
예를 들면 특정 서비스에서 이메일(X)과 닉네임(Y)의 관계일 수 있다.
X를 알면 Y를 유일하게 찾아낼 수 있기 때문이다.
추가로 우리가 사용할 함수형 종속에 대한 명제들인 암스트롱 공리는 아래와 같다.
아래에서 X, Y, Z는 모두 한 테이블의 칼럼이다.
- 자기 종속(Self-Determination) - 컬럼은 언제나 스스로에게 함수 종속적이다.
$$X → X$$
- 반사의 공리(Reflexivity Rule)
$$X\supseteq Y \Rightarrow \!\, X → Y$$
- 확대의 공리(Augmentation Rule)
$$X→Y \Rightarrow \!\, XZ → YZ$$
- 이행의 공리(Transitivity Rule)
$$X→Y \wedge Y→Z \Rightarrow \!\, X → Z$$
- 합집합/분해 공리(Union/Decomposition Rule)
$$X→Y \wedge X→Z ⇔ X → YZ$$
한 줄 한 줄 가만히 살펴보면 당연한 말만 써놨지만, DB 정규화의 기준이 되기 때문에 알고 있어야 한다.
계속해서 정규화의 목적과 원칙, 그리고 과정에 대해 정리하고 넘어가자.
- 목적
- 중복 방지 및 제거로 인한 이상현상 방지
- DB의 구조적 안정성 강화(정제)
- 모든 스키마의 자유로운 표현
- 효과적인 CRUD와 그 실행 시 테이블 재구성 필요성을 줄임
- 원칙
- 데이터의 맥락과 의미 유지 ↔ 무손실 분해와 비부가적 조인
- 중복 제거
- 하나의 테이블은 하나의 주제만 소유(분리 가능한 테이블은 분리)
- 과정
- 컬럼과 그 함수형 종속성을 수집 <F+> - 기존 종속에 암스트롱 공리로 분석한 함수형 종속을 추가한 집합
- 제약조건을 지키며 비정규 테이블 분할 → 스키마 정제
First Normal Form
제1 정규형(1NF)은 테이블의 모든 값이 원자값을 갖는 형태이다.
여기서 원자값이란 더 이상 쪼갤 수 없는 값을 말하며, 조금 애매한 정의이기 때문에 아래와 같은 정의를 사용하기도 한다.
- 열에는 위-아래의 순서가 없다.
- 행에는 좌-우의 순서가 없다.
- 중복되는 열이 없다.
- 테이블의 한 칸에는 하나의 값만 들어간다.
- 모든 행은 규칙적이다(숨어있는 요소(행)를 가지지 않는다).
즉, 한 칸에 복수의 값을 가져선 안 된다. 위 정의에 맞도록 정규화를 진행하는 예는 아래와 같다.

왼쪽 테이블에선 아래와 같은 문제가 발생할 가능성이 있으며,
- 갱신 이상 - 토끼의 이름이 보라로 바뀌면 같이 있던 고양이도 이름이 바뀌어 버린다.
- 삭제 이상 - 해달이 테이블에서 이름을 삭제하면 같이 있던 고양이의 이름도 삭제되어 버린다.
더 이상 분해할 수 없을 때까지 데이터를 나눈 뒤에 새로운 식별자를 부여했다.
Second Normal Form
2NF는 테이블이 1NF를 만족한다는 가정에서 출발한다.
1NF에 더해 2NF는 모든 컬럼이 완전 함수적 종속을 갖기를 요구한다.
여기서 완전 함수적 종속이란 쉽게 말해 하나의 PK로 컬럼의 값을 식별할 수 있어야 한다는 것이다.
말로 하면 꼬이니까 예를 들어보자.

위 테이블의 PK는 (ID, 수업)의 복합키이다. 따라서 ID와 수업을 조합하면 이름과 강의실을 알아낼 수 있다.
그런데 잘 보면 PK의 부분집합인 수업만 알고 있어도 강의실이 결정되는 것을 확인할 수 있는데, 이를 부분 함수적 종속이라고 한다.
발생할 수 있는 이상은 아래와 같다.
- 삽입 이상 - 수업을 듣는 학생을 추가하려면 불필요한 정보(반장)가 추가되어야 한다.
- 갱신 이상 - 물리 수업의 반장이 바뀌는 경우 전부 찾아 변경하지 않으면 모순이 발생한다.
- 삭제 이상 - 건담이 역사 수업을 듣지 않기로 했다. 이때 반장의 정보까지 같이 사라져 버린다.
2NF는 이와 같은 상황에서 테이블을 분리해 부분 함수적 종속을 제거하기를 요구한다.

분리의 결과로 부분 함수적 종속이 제거되어 2NF를 만족하는 것을 확인할 수 있다.
Third Normal Form
3NF는 마찬가지로 2NF를 만족한 상태에서 시작한다.
위에서 살펴봤던 함수적 종속의 종류 중에 이행의 공리라는 것이 있었다.
$$X \to Y \wedge Y \to Z \Rightarrow \!\, X \to Z$$
3NF는 2NF 상태의 테이블에게 위와 같은 이행적 종속을 제거할 것을 요구한다.
예를 들면 아래와 같다.

위 테이블의 경우 전형적인 이행적 종속을 보이고 있다.
$$이름 \to 수업 \wedge 수업 \to 수강료 \Rightarrow \!\, 이름 \to 수강료$$
이런 경우 생길 수 있는 이상은 아래와 같다.
- 삽입 이상 - 수업을 듣는 학생을 추가할 때마다 수강료 데이터의 중복이 발생한다.
- 갱신 이상 - 건희가 도단이를 따라 수학 수업을 들으려다 같은 수업을 5천 원 비싸게 듣는 상황이 발생할 수 있다.
- 삭제 이상 - 아인이가 수업을 취소하는 경우 역사수업에 대한 정보가 사라져 버린다.
개발자는 갱신 이상을 방지하기 위해 수업이 바뀔 때 수강료도 변경하도록 로직을 짜는 작업을 하는데,
바로 이런 번거로움과 실수 가능성을 끊기 위한 것이 3NF이다.
결과는 아래와 같다.

일반적으로 여기까지만 진행해도 꽤 효율적인 스키마가 완성된다.
Boyce Codd Normal Form
BCNF는 3.5NF 혹은 Strong 3NF라고 불린다.
BCNF는 3NF에 더해 모든 과잉된 함수형 종속을 제거할 것을 요구한다.
이는 한 마디로 요약하면 모든 결정자는 키에 속해있어야 한다는 문장으로 정리할 수 있다.
혹은 슈퍼키에 속하지 않은 결정자는 존재해선 안된다고 바꿔 말할 수도 있겠다.
Super Key
키는 말 그대로 식별자 기능을 할 수 있는 하나 또는 그 이상의 컬럼의 집합이다.

- 슈퍼키 - 테이블의 각 행을 유일하게 식별할 수 있는 하나 이상의 컬럼의 집합이다. 유일성을 만족한다.
- 후보키 - 슈퍼키 중에서 최소성을 만족하는 컬럼의 집합이다.
- 기본키 - 후보키 중 하나로 최소성과 유일성을 만족하는 컬럼이다. 테이블 별로 오직 하나만 지정할 수 있다.
추가로 null값을 가질 수 없고, 당연히 중복된 값을 가질 수도 없다. - 대체키 - 기본키로 선택되지 않은 후보키를 말한다. 기본키와 동일한 속성을 지니며 대체도 가능하다.
- +) 외래키 - 다른 테이블을 참조하기 위해 해당 테이블의 기본키를 이용해 지정한다.
참조 관계 시 부모테이블이 먼저 생성되어야 하고, 자식 테이블이 먼저 삭제되어야 한다.
계속해서 예를 들어보자.

위와 같은 테이블에서 PK는 (이름, 수업)이고, 이는 교수를 특정 짓고 있다.
그런데 가만 보면 교수 역시 거꾸로 수업을 결정하고 있는데, 문제는 교수 컬럼이 슈퍼키가 아니라는 것이다.
즉 수업에 대한 결정자가 슈퍼키에 속하지 않는다는 뜻이다.
이때 생길 수 있는 이상은 아래와 같다.
- 삽입 이상 - 건희가 추가로 수학 수업을 들을 경우, 교수 데이터의 중복이 발생한다.
- 갱신 이상 - B 교수의 담당 수업이 디자인으로 바뀌면 도단이의 수강 수업이 함께 변경된다.
- 삭제 이상 - 딩거가 수업을 취소하는 경우 컴퓨터 과목의 담당 교수 정보가 함께 삭제된다.
따라서 이를 BNCF의 요구사항에 맞춰 분해해야 할 필요가 생기는데, 결과는 아래와 같다.

테이블 분할로 인해 모든 결정자가 슈퍼키, 그중에서도 후보키가 된 것을 확인할 수 있다.
이로써 모든 불필요한 함수형 종속이 제거되며, 실무에서는 BCNF 수준의 정규화를 많이 사용한다고 한다.
Fourth Normal Form
4NF는 BCNF를 만족한 상태에서 시작한다.
4NF의 요구사항은 DB에서 다치 종속성을 제거하는 것인데
다치 종속성은 하나의 칸에 여러 개의 값이 들어가는 것을 가리키며, 보통 세 개 이상의 컬럼 집합이 존재할 때 나타난다.
기호로는 아래와 같이 나타낸다.
$$X \twoheadrightarrow Y \mid Z$$
잘 안 보일 수도 있는데, 머리가 두 개 달린 화살표이다. 테이블로 확인하면 아래와 같다.

먼저 함수 종속성을 확인한 후 정규화를 진행했다.
정규화가 끝난 테이블은 세 개의 칼럼으로 구성된 기본키를 가지며, 다른 함수적 종속이 존재하지 않기 때문에 BCNF이다.
하지만 데이터가 중복 저장되는 문제와 함께 건희의 술 취향이 추가된다면 세 개의 행을 새로 삽입해야 하는 문제가 존재한다.
문제 발생의 원인을 찾아보면 과목과 주종 사이에 어떤 관계도 존재하지 않는다는 것이 눈에 띈다.
즉, 아무 연관이 없는 두 개의 1:N 관계를 하나의 테이블에 몰아넣었기 때문에 위와 같은 문제가 발생하는 것이다.
계속해서 다치 종속성
$$X \twoheadrightarrow Y$$
가 다음과 같은 조건을 만족하면 이를 단순 다치 종속성(Trivial MVD)이라고 부른다.
$$X \supseteq Y \lor X \cup Y = R$$
여기서 R은 전체 테이블을 뜻한다. 만약 테이블의 모든 다치 종속성이 단순 다치 종속이라면,
해당 테이블은 4NF 조건을 만족시킨다고 할 수 있다.
하지만 단순 다치 종속이 아닌 비단순 다치 종속이라면 위와 같이 모든 컬럼이 기본키가 되는 경우가 생기므로
아래와 같이 분해해야 할 필요가 생긴다.

위의 조건에 따라 각 테이블의 다치 종속은 단순 다치 종속이며, 4NF를 만족하는 것을 확인할 수 있다.
추가로 일반적으로 모든 테이블은 4NF 형태로 전환될 수 있다고 한다.
Fifth Normal Form
5NF는 테이블에서 후보키를 통하지 않은 조인 종속성을 제거할 것을 요구한다.
여기서 조인 종속성이란 쪼개진 테이블을 적절히 조인하면 원래 테이블을 만들어낼 수 있는 관계를 말한다.
즉 테이블을 적절하게 쪼개고(Project) 합치며(Join) 중복성을 제거하는 데 목적이 있으며,
이 때문에 5NF는 PJNF라고도 불린다.
5NF에서 테이블의 조인 종속성은 무손실 분해와 비부가적 조인으로 구성되는데, 이는 각각 아래와 같다.
- 무손실 조인 분해(Lossless Project) - 분해 과정에서 데이터가 사라지지 않아 추후 특정 키로 조인할 때 테이블 복원이 가능함
- 비부가적 조인(Nonadditive Join) - 조인 결과에 원래 테이블에는 없는 행이 추가되지 않음
이어서 후보키란 위에 적었듯이 PK의 후보가 되며 유일성과 최소성을 만족하는, 하나 이상의 컬럼의 집합이다.
이를 통하지 않는 조인 종속성이란 어떤 것이 있을까? 테이블로 살펴보자.
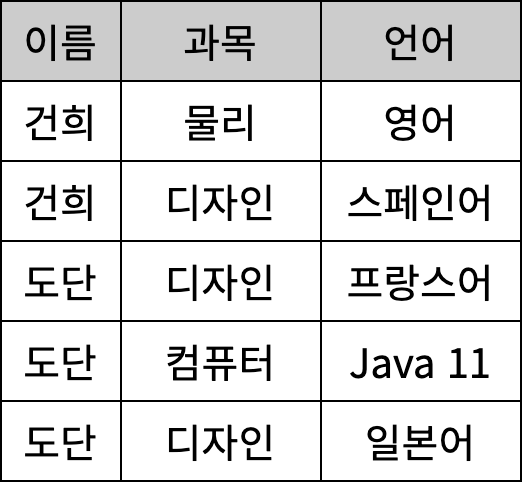
위 테이블에서 (건희, 도단이) ↔ 과목, (건희, 도단이) ↔ 언어 사이엔 연관성이 존재하지만 과목 ↔ 언어 사이는 그렇지 않다.
하지만 여기에 과목 ↔ 언어 사이에도 연관성이 있다고 가정하면 후보키가 아닌 (이름, 과목)에 대해서도
조인 종속성이 발생한다. 이 경우 테이블을 아래와 같이 분해할 수 있다.

조인 종속성이 사실상 제거된 것을 확인할 수 있다.
하지만 이와 같은 조인 종속성을 발견하는 일은 비용이 많이 드는 일이기 때문에 실무에서는 잘 쓰이지 않는다고 한다.
추가로 BCNF와 4NF 사이엔 EKNF가, 4NF와 5NF 사이에는 ETNF가, 5NF 이후로는 DKNF와 6NF가 존재한다.
Summary
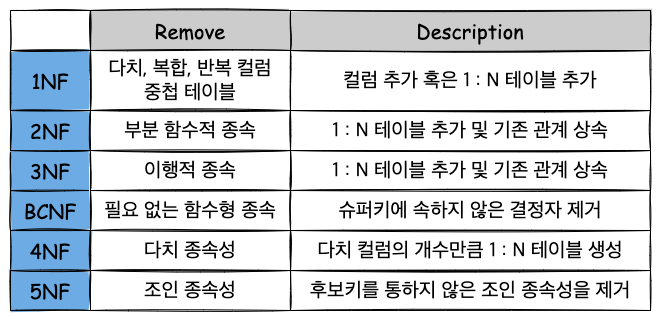
- 정규화의 목적은 DB 효율성 극대화(CRUD 비용 감소)이다. 즉, 가능한 빠른 단계에서 검토해야 한다.
- 이어서 효율성을 가장 크게 해치는 데이터의 중복을 적절한 테이블 분할로 제거한다.
- 분해 과정에서 무손실 분해와 비부가적 조인은 언제나 원칙으로 삼아야 한다.
- 정규화 따라 정해진 메모리에 저장할 수 있는 데이터의 양이 늘어나 캐시의 적중률이 상승하기도 한다.
- 정규화는 함수 종속성(1~BCNF) → 다치 종속성(4NF) → 조인 종속성(5NF) 순으로 제거하며 보통 함수 종속성 제거까지 수행한다.
- 정규화가 진행될수록 테이블의 개수가 늘어나 JOIN의 비용이 정규화의 장점을 앞서는 경우,
중복을 허용하더라도 정규화 단계를 낮추고 테이블을 다시 병합하는 것이 나은 경우가 생긴다. 이를 반(역/비) 정규화라고 부른다.
'Development > Technical Interview' 카테고리의 다른 글
| [면접 준비 - Database]외래 키(Foreign Key, FK)에 대하여 (5) | 2023.01.02 |
|---|---|
| [면접 준비 - CS]컴퓨터 부팅 과정 (1) | 2022.12.29 |
| [면접 준비 - Network]웹 애플리케이션의 작동 흐름 (6) | 2022.12.28 |
| [면접 준비 - Database]데이터 무결성, 데이터 무결성 제약조건 (1) | 2022.12.27 |
| [면접 준비 - Database]DB 설계, 스키마 3계층 (3) | 2022.12.27 |
| [면접 준비 - Java]서블릿(Servlet)에 대하여 (2) | 2022.12.26 |
- Total
- Today
- Yesterday
- 유럽
- 세계일주
- Algorithm
- 세모
- 칼이사
- Python
- a6000
- 스프링
- 지지
- 리스트
- Backjoon
- 백준
- 유럽여행
- 야경
- 여행
- 남미
- RX100M5
- BOJ
- 면접 준비
- spring
- 스트림
- 알고리즘
- java
- 동적계획법
- 기술면접
- 중남미
- 맛집
- 자바
- 세계여행
- 파이썬
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
