Chapter 4: Fitting probability models(2)

목차

 

4.4 예제 1: 단변량 정규 분포 (Univariate Normal)

 

앞서 설명한 개념들을 구체적으로 보여주기 위해, 

 

단변량 정규 모델(univariate normal model)을 스칼라 데이터 ${x_i}_{i=1}^I$에 피팅하는 예제를 다룬다.

단변량 정규 모델의 확률 밀도 함수(pdf)는 다음과 같다:

 

$$Pr(x|μ,σ^2)=\text{Norm}_x[μ,σ^2]=\frac{1}{\sqrt{2πσ^2}}\text{exp}(-\frac{1}{2}⋅\frac{(x−μ)^2}{σ^2})\tag{4.7}$$

 

이 모델은 두 개의 매개변수를 가진다:

• 평균(mean) $\mu$
• 분산(variance) $\sigma^2$

이제 평균 $\mu = 1$, 분산 $\sigma^2 = 1$인 단변량 정규 분포로부터 

 

$I$개의 독립적인 데이터 포인트 $x_1, \dots, x_I$를 생성한다고 가정하자.

 

이때의 목표는, 주어진 데이터로부터 $\mu$와 $\sigma^2$를 다시 추정(피팅)하는 것이다.

 

4.4.1 최대 우도 추정 (Maximum Likelihood Estimation)

그림 4.1 단일 데이터 포인트에 대한 우도는 해당 위치에서의 pdf 높이(파란 수직선)이다. 전체 데이터셋에 대한 우도는 이 개별 우도들의 곱이다. (a) 분산이 커서 pdf 전체가 낮음 → 우도 낮음 (b) 한 데이터가 극단적 → 해당 모델 하에서 우도 매우 낮음 (c) <최대 우도 피팅>: 우도를 최대로 만드는 ${\mu, \sigma^2}$ 조합

 

그림 4.2 고정된 데이터에 대해 우도는 $\mu$, $\sigma^2$에 대한 함수이다. 다양한 파라미터 조합이 가능하지만, 그 중에서 가장 타당한 해는 우도가 최대인 지점(녹색 십자)이다.

 

관측된 데이터 ${x_i}_{i=1}^I$에 대해, 매개변수 ${\mu, \sigma^2}$의 우도(likelihood)는 

 

각 데이터 포인트에 대해 확률 밀도 함수를 평가한 뒤 곱을 취함으로써 계산된다:

 

$$\begin{align*} Pr(x_{1...I}|μ,σ^2) &= \prod^{I}_{i=1}\text{Norm}_{x_i}[μ,σ^2] \\ &= \frac{1}{(2πσ^2)^{I/2}}\text{exp} \left ( -\frac{1}{2σ^2}\sum_{i=1}^I(x_i−μ)^2 \right ) \end{align*}\tag{4.8}$$

 

당연히 어떤 매개변수 쌍 ${\mu, \sigma^2}$는 다른 쌍들보다 더 높은 우도 값을 가진다 (그림 4.1).

 

이 우도는 평균 $\mu$와 분산 $\sigma^2$에 대한 2차원 함수로 시각화될 수 있으며 (그림 4.2),

 

최대 우도 해 $\hat{\mu}, \hat{\sigma}^2$는 이 표면에서 최고점에서 발생한다:

 

$$\hat{μ},\hat{σ}^2=\underset{μ,σ^2}{\text{argmax}} \left [ Pr(x_{1...I}|μ,σ^2) \right ]\tag{4.9}$$

 

그림 4.3 로그 함수는 단조 증가 함수이므로, 어떤 지점이 더 높았다면 로그를 취해도 여전히 더 높다. 즉, 로그 우도 공간에서도 최댓값의 위치는 동일하게 유지된다.

원칙적으로는 식 (4.8)을 $\mu$와 $\sigma^2$에 대해 미분하고 0으로 놓아 풀 수 있다.

 

그러나 실제로는 수식이 복잡해지므로, 로그 우도(log-likelihood) $L$을 대신 사용한다.

 

로그 함수는 단조 증가 함수이므로 (그림 4.3), 함수의 최대값 위치는 로그 변환 후에도 변하지 않는다.

 

로그 우도는 다음과 같이 전개된다:

 

$$\begin{align*} L &= \text{log}\,Pr(x_{1...I}|μ,σ^2) \\ &= \sum_{i=1}^{I}\text{log}\,\text{Norm}_{x_i}[μ,σ^2] \\ &= -\frac{I}{2}\text{log}(2π)-\frac{I}{2}\text{log}σ^2-\frac{1}{2σ^2}\sum_{i=1}^{I}(x_i−μ)^2 \end{align*}\tag{4.10}$$

 

평균에 대한 미분

 

로그 우도를 $\mu$에 대해 미분하고 0으로 두면 다음을 얻는다:

 

$$ \frac{\partial L}{\partial μ} = \frac{1}{σ^2}\sum_{i=1}^{I}(x_i−μ)=0 \tag{4.11}$$

$$\Rightarrow \hat{μ}=\frac{1}{I}\sum_{i=1}^{I}x_i\tag{4.12}$$

 

분산에 대한 추정

 

동일한 방식으로, 분산에 대한 최대 우도 해는 다음과 같이 주어진다:

 

$$\hat{σ}^2=\frac{1}{I}\sum_{i=1}^{I}(x_i−\hat{μ})^2\tag{4.13}$$

 

이 결과는 직관적이며 놀랍지 않다. 

 

그러나 이 방식은 다른, 더 복잡한 분포에서도 파라미터를 추정하는 데 사용될 수 있다.

 

최소제곱 피팅 (Least Squares Fitting)

 

참고로, 많은 문헌에서는 피팅을 최소제곱법(least squares) 관점에서 설명한다.

 

정규 분포의 평균 $\mu$만을 ML 방식으로 피팅한다고 가정하면, 다음과 같은 수식 전개를 통해

 

제곱합을 최소화하는 형태로 표현할 수 있다:

 

$$\begin{align*} \hat{μ} &= \underset{μ}{\text{argmax}}\left ( -\frac{1}{2σ^2}\sum_{i=1}^I(x_i−μ)^2 \right ) \\ &= \underset{μ}{\text{argmin}}\sum_{i=1}^I(x_i−μ)^2  \end{align*}\tag{4.14}$$

 

즉, 최소제곱 피팅은 정규 분포의 평균을 ML로 피팅하는 것과 정확히 동일하다.

 

요약

• ML 피팅은 우도 함수를 최대화하는 파라미터 조합을 찾는 방식이다.
• 정규 분포의 경우, $\mu$와 $\sigma^2$에 대한 폐형 해(closed-form solution)를 유도할 수 있다.
• 로그 우도를 사용하면 계산이 간단해지고, 데이터 포인트들의 독립성도 더 쉽게 활용된다.
• ML로 평균을 피팅하는 문제는 최소제곱 피팅과 동일하다.

4.4.2 최대 사후 확률 추정 (Maximum a Posteriori Estimation)

 

이제 정규 분포의 파라미터에 대해 최대 사후 확률(MAP) 피팅을 시도한다.

 

MAP에서는 사후 확률 $Pr(\mu, \sigma^2 | x_1, \dots, x_I)$를 최대화하는 $\mu$, $\sigma^2$를 찾는다.

 

목표 함수는 다음과 같이 정의된다:

 

$$\hat{μ},\hat{σ}^2=\underset{μ,σ^2}{\text{argmax}} \left [  \prod^{I}_{i=1}Pr(x_i|μ,σ^2)⋅Pr(μ,σ^2) \right ]\tag{4.15}$$

 

우도 $Pr(x_i|\mu, \sigma^2)$는 정규 분포이고,

 

사전 분포 $Pr(\mu, \sigma^2)$는 정규-역감마 분포(normal-inverse-gamma distribution)를 선택하였다.

 

이 사전은 정규 분포에 대해 켤레 사전(conjugate prior)이기 때문에 계산이 간단해진다.

 

그림 4.4 a) $\alpha, \beta, \gamma = 1$, $\delta = 0$인 정규-역감마 분포는 정규 분포의 파라미터에 대한 넓은 사전 분포를 형성한다. 자홍색 십자는 사전 분포의 모드를 나타내며, 파란색 십자들은 이 분포로부터 샘플링한 5개의 파라미터 쌍이다. b) 이 샘플들은 각각의 정규 분포로 시각화된다.

 

정규-역감마 사전 분포의 수식은 다음과 같다:

 

$$Pr(μ,σ^2)=\sqrt{\frac{γ}{2πσ^2}}⋅\frac{β^α}{Γ(α)}⋅\frac{1}{(σ^2)^{α+1}}⋅\text{exp}\left [ -\frac{2β+γ(δ−μ)^2
}{2σ^2} \right ]\tag{4.16}$$

 

그림 4.5 a) 데이터로부터 계산한 우도 함수 b) 정규-역감마 사전 분포 c) 이 둘의 곱이 사후 분포에 비례하며, 그 최고점에 위치한 청록색 십자가 MAP 추정치이다. 이는 최대 우도 추정치(녹색)와 사전의 모드(자홍색) 사이에 위치한다.

 

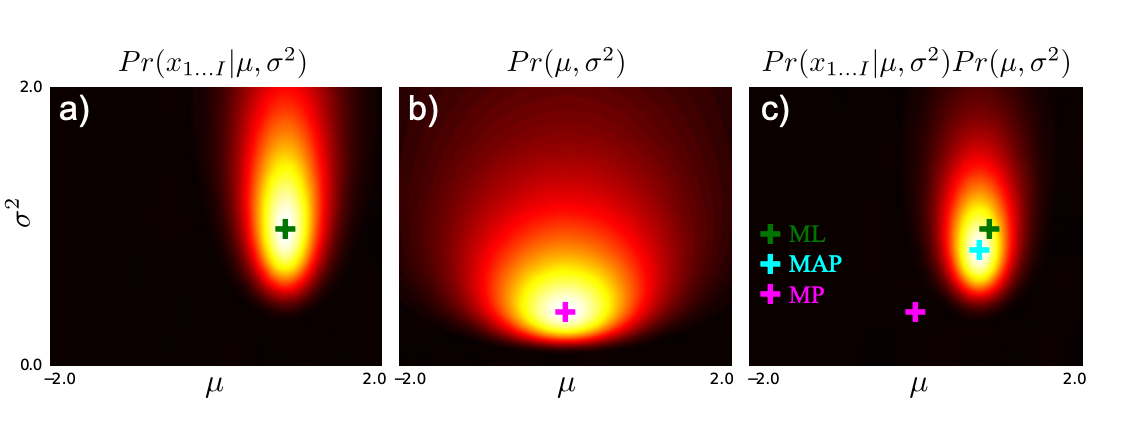
사후 분포는 우도와 사전의 곱에 비례하며 (그림 4.5),

데이터에 잘 들어맞고, 동시에 사전적으로도 가능성 높은 파라미터 조합에서 가장 높은 값을 가진다.

앞서 최대 우도 추정과 마찬가지로, 로그를 취하면 계산이 간단해진다:

 

$$\hat{μ},\hat{σ}^2=\underset{μ,σ^2}{\text{argmax}}\sum_{i=1}^I\log{Pr(x_i|μ,σ^2)}+\log{Pr(μ,σ^2)}\tag{4.17}$$

 

이제 로그 사후 확률을 $\mu$, $\sigma^2$에 대해 각각 미분하고 0으로 놓아 정리하면 

 

다음과 같은 폐형 해(closed-form solution)를 얻는다:

 

$$\hat{μ}=\frac{\sum_{i=1}^Ix_i+γδ}{I+γ},\quad\hat{σ}^2=\frac{\sum_{i=1}^I(x_i-\hat{μ})^2++2β+γ(δ−\hat{μ})^2 }{I+3+2α}\tag{4.18}$$

 

평균에 대한 식은 다음과 같이 해석하기 쉽도록 다시 쓸 수 있다:

 

$$\hat{μ}=\frac{I\bar{x}+γδ}{I+γ}$$

 

이는 두 항의 가중합(weighted sum)이다:

• 첫 번째 항: 데이터 평균 $\bar{x}$, 가중치는 데이터 개수 $I$
• 두 번째 항: 사전 평균 $\delta$, 가중치는 사전 하이퍼파라미터 $\gamma$

그림 4.6 (a) MAP 추정값(청록색 십자)은 최대 우도 추정값(녹색 십자)과 사전 분포의 최고점(자주색 십자) 사이에 위치한다. (b) MAP 추정값, ML 추정값, 사전 최고점 각각에 해당하는 정규 분포를 시각화한 결과이다. (c–d) 데이터 포인트의 수가 줄어들수록, 사전 분포의 영향력이 증가하여 추정 결과가 사전에 더 가까워진다. (e–f) 데이터가 단 하나뿐인 경우, 최대 우도 추정은 분산을 계산할 수 없기 때문에 정의되지 않는다. 그러나 MAP 추정은 사전 분포 덕분에 여전히 유효한 추정값을 계산할 수 있다.

 

이 결과는 MAP 추정의 성질을 잘 보여준다 (그림 4.6):

• 데이터가 많을수록: $\hat{\mu}$는 거의 $\bar{x}$와 같아져 ML 추정과 유사해진다.
• 데이터가 적을수록: $\hat{\mu}$는 $\bar{x}$와 $\delta$의 중간값이 된다.
• 데이터가 전혀 없을 때: 추정값은 전적으로 사전에 의존하게 된다.
• 하이퍼파라미터 $\gamma$는 사전 분포의 <신뢰 강도>를 조절하는 역할을 하며, $\mu$에 대한 사전의 영향력을 결정한다.

분산에 대해서도 유사한 결론이 도출된다.

 

한 가지 흥미로운 점은, 데이터가 단 하나일 경우이다 (그림 4.6e–f 참고):

• 이 경우, ML 추정에서는 분산 $\hat{\sigma}^2 = 0$이 되어,무한히 얇고 무한히 높은 정규 분포가 만들어지게 된다.
• 이는 해당 데이터에 대해 무한한 우도를 부여하는 비현실적인 결과이다.
• 그러나 MAP 추정은 여전히 합리적인 분산 값을 산출하며, 이는 사전 분포가 극단적인 모델을 방지해주기 때문이다.

요약

• MAP 추정은 사전 분포와 데이터로부터 얻은 정보를 모두 고려하는 방법이다.
• 사전 분포는 극단적인 파라미터 추정을 방지하고, 데이터가 적을 때 더 큰 영향을 발휘한다.
• 정규 분포에 대해 정규-역감마 사전을 사용하면, 평균과 분산의 MAP 해를 명시적 수식으로 얻을 수 있다.
• ML과 달리 MAP는 단일 데이터 상황에서도 안정적이며 현실적인 결과를 제공한다.

4.4.3 베이지안 접근 (The Bayesian Approach)

 

베이지안 접근에서는 데이터 ${x_i}_{i=1}^I$로부터 베이즈 정리를 사용해 

 

매개변수 $\mu$, $\sigma^2$에 대한 사후 분포 $Pr(\mu, \sigma^2 \mid x_1, \dots, x_I)$를 계산한다:

 

$$Pr(μ,σ^2|x_{1...I})=\frac{\prod^{I}_{i=1}Pr(x_i|μ,σ^2)⋅Pr(μ,σ^2)}{Pr(x_{1...I})}\tag{4.20}$$

 

여기서,

• $Pr(x_i \mid \mu, \sigma^2)$는 정규 분포 (likelihood),
• $Pr(\mu, \sigma^2)$는 정규-역감마 분포(normal-inverse-gamma)로 설정된 사전 분포이다.

켤레 사전(conjugate prior)을 사용했기 때문에, 사후 분포 역시 정규-역감마 분포의 형태를 가진다:

 

$$Pr(μ,σ^2|x_{1...I})=\text{NormInvGam}_{μ,σ^2}[\tilde{α},\tilde{β},\tilde{γ},\tilde{δ}]\tag{4.22}$$

 

여기서 새로운 하이퍼파라미터는 다음과 같이 갱신된다:

 

$$\begin{align*} \tilde{α} &= α+\frac{I}{2} \\ \tilde{γ} &= γ+I \\ \tilde{δ} &= \frac{γδ+∑x_i}{γ+I} \\ \tilde{β} &= \frac{1}{2}∑x_i^2+β+\frac{γδ^2}{2}-\frac{(γδ+∑x_i)^2}{2(γ+I)} \end{align*}\tag{4.21}$$

 

이 결과는 켤레 사전의 주요 장점을 보여준다:

 

사후 분포를 폐형식(closed-form)으로 표현할 수 있다.

 

사후 분포의 해석

 

이 사후 분포는 다양한 $(\mu, \sigma^2)$ 조합이 데이터를 생성했을 상대적인 가능성을 나타낸다.

 

분포의 최고점에는 MAP 추정값이 존재하지만, 그 외에도 많은 가능성 있는 조합이 존재한다 (그림 4.6).

 

• 데이터가 풍부할 때 (그림 4.6a):
  사후 분포는 좁고 집중적이며, MAP 추정과 베이지안 추정이 거의 일치한다.
  이 경우, 단일 추정값에 모든 확률 질량을 집중시키는 근사가 유효하다.
  
  
• 데이터가 부족할 때 (그림 4.6c):
  다양한 파라미터가 데이터를 설명할 수 있으므로 사후 분포가 넓고 평탄해진다.
  이 경우에는 단일 추정값만 사용하는 MAP 접근이 부적절하다.

예측 분포 (Predictive Density)

 

ML이나 MAP 접근에서는 새로운 데이터 $x^*$의 예측 확률을, 

 

추정된 $\hat{\mu}$와 $\hat{\sigma}^2$를 이용해 정규 분포로부터 직접 계산한다.

반면 베이지안 접근에서는 모든 가능한 파라미터 조합에 대해 예측을 수행하고, 사후 분포로 가중 평균을 수행한다:

 

$$Pr(x^*|x_{1...I})=\iint Pr(x^*|μ,σ^2)⋅Pr(μ,σ^2|x_{1...I})dμdσ^2\tag{4.23}$$

 

이 적분은 다시 한 번 켤레 사전을 이용해 계산할 수 있으며, 결과는 다음과 같다:

 

$$Pr(x^*|x_{1...I})=κ(x^*;\tilde{α},\tilde{β},\tilde{γ},\tilde{δ})\tag{4.24}$$

 

여기서 $\kappa$는 예측 분포를 계산하는 데 필요한 상수로, 아래와 같이 구해진다:

 

$$\begin{align*} \breve{α} &= \tilde{α}+\frac{1}{2} \\ \breve{γ} &= \tilde{γ}+1 \\ \breve{δ} &= \frac{\tilde{γ}\tilde{δ}+x^*}{\tilde{γ}+1} \\ \breve{β} &= \frac{1}{2}x^{*2}+\tilde{β}+\frac{\tilde{γ}\tilde{δ}^2}{2}-\frac{(\tilde{γ}\tilde{δ}+x^*)^2}{2(\tilde{γ}+1)} \\ κ(x^*) &= \frac{1}{\sqrt{2\pi}}⋅\frac{\sqrt{\tilde{γ}/\tilde{β}^{\tilde{α}}}}{\sqrt{\breve{γ}/\breve{β}^{\breve{α}}}}⋅\frac{Γ[\breve{α}]}{Γ[\tilde{α}]} \end{align*}\tag{4.25-4.26}$$

 

두 번째 장점: 이와 같이 켤레 사전을 사용하면 예측 분포도 폐형식으로 계산 가능하다.

 

그림 4.7 a) 사후 확률 분포 b) 해당 분포로부터 샘플링된 여러 파라미터 조합 c) 베이지안 예측 분포는 이 무한한 정규 분포들의 평균이며, 사후 확률로 가중되어 계산된다.

 

그림 4.7은 베이지안 예측의 구조를 시각적으로 이해하는 데 핵심적인 역할을 한다. 

 

각각의 서브그림은 베이지안 예측이 단일 파라미터 추정에 기반한 MAP 방식과 어떻게 다른지를 보여준다.

a) 사후 분포

• 이 그래프는 파라미터 공간 $(\mu, \sigma^2)$ 상에서의 사후 확률 분포를 보여준다.
• 진한 영역일수록 데이터에 잘 맞고 사전 분포에도 부합하는 파라미터 조합이다.
• MAP 추정은 이 분포의 최고점에 해당한다.

b) 샘플링된 정규 분포들

• 사후 분포에서 파라미터들을 샘플링하면, 각각의 샘플은 특정한 정규 분포 곡선으로 시각화된다.
• 이는 데이터에 대해 가능한 여러 설명(모델들)이 존재함을 의미한다.

c) 베이지안 예측 분포

• 베이지안 예측 분포는 위의 모든 가능한 정규 분포들의 가중 평균이다.
• 가중치는 사후 확률 분포에 기반하며, 단일 추정값이 아닌 분포 전체를 고려한다.
• 이는 더 온건하고 보수적인 예측, 즉 신뢰 구간이 넓고 꼬리가 긴 분포를 만들어낸다.

➡️ 핵심 포인트:

 

베이지안 예측은 "단일 정답"이 아니라 "가능성들의 합성"이다. 

 

이는 특히 데이터가 적거나 불확실성이 클 때 강력한 장점으로 작용한다.

그림 4.8 a–c) 학습 데이터 개수 50, 5, 1에 대한 MAP과 베이지안 예측 분포 비교 데이터가 줄어들수록 베이지안 분포는 꼬리가 두꺼워지고, MAP 분포는 과도하게 자신감 있는 형태를 유지함. d–f) 로그 스케일로 나타내면 이러한 차이가 더욱 명확하게 드러남

 

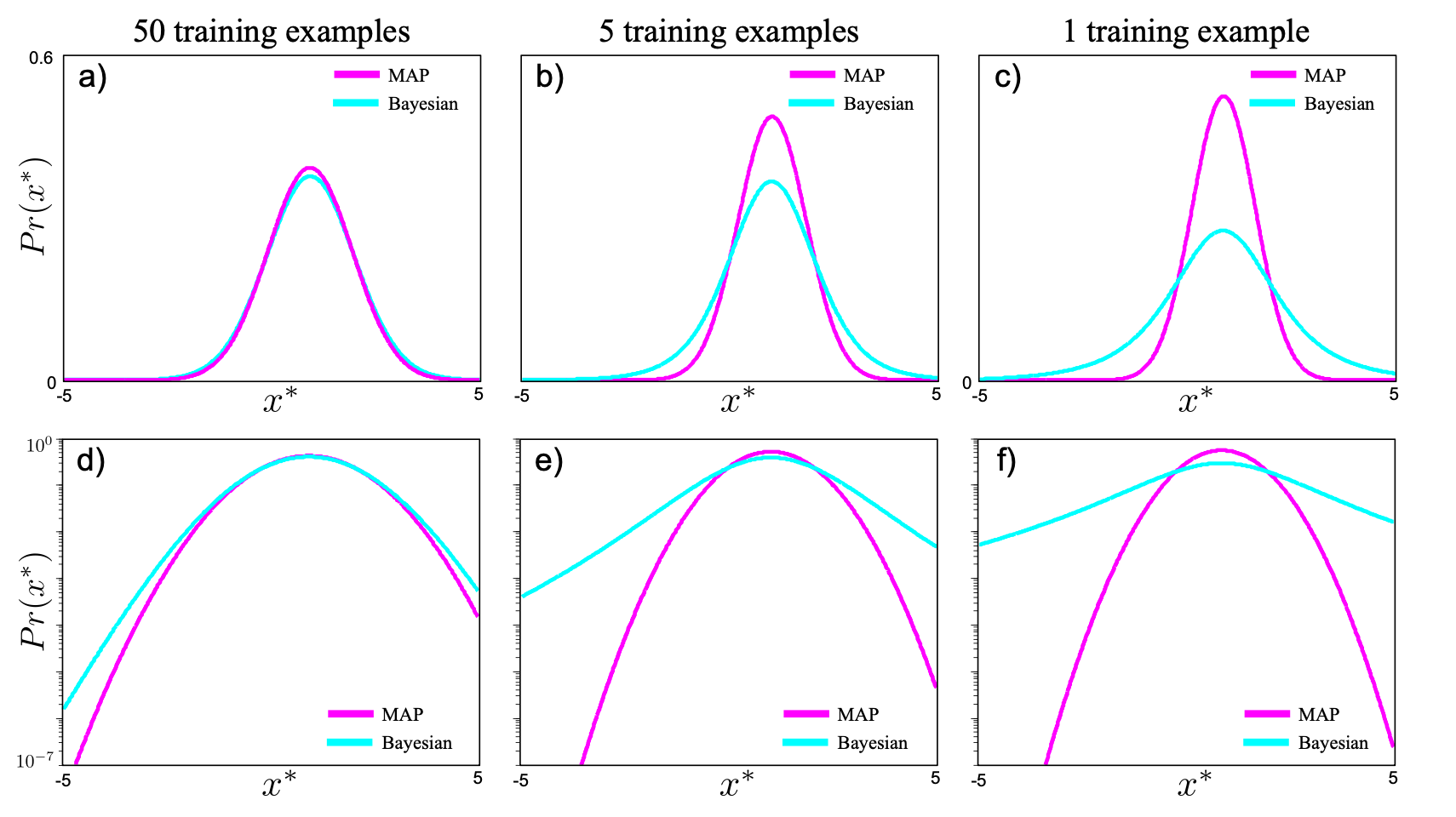
그림 4.8은 베이지안 접근과 MAP 접근 간의 예측 분포 차이를 명확하게 보여준다.

a–c) 학습 데이터 수: 50, 5, 1

• 각각의 경우에 대해, 베이지안과 MAP 방식으로 계산된 **예측 분포(정규 곡선)**를 비교한다.
• 데이터가 많을수록 두 방식의 결과는 유사하지만,
  데이터가 줄어들수록 MAP는 과도하게 좁고 자신감 있는 예측을 한다.
• 반면 베이지안은 꼬리가 더 두꺼운 분포, 즉 불확실성을 반영한 형태를 유지한다.

d–f) 로그 스케일 시각화

• 같은 분포를 로그 스케일로 보면, MAP 분포는 예측 외 영역에서 매우 낮은 값을 보여 과도한 확신을 드러낸다.
• 베이지안 분포는 더 완만하게 감소하며, 미지의 데이터에 대한 여지를 남긴다.

➡️ 핵심 포인트:

 

데이터가 적을 때 MAP는 오버피팅, 베이지안은 보수적 예측.

 

이러한 차이는 특히 이상치(outlier)나 분포 외 샘플을 다룰 때 중요한 차이를 만들어낸다.