Chapter 4: Fitting probability models(3)

목차

 

4.5 예제 2: 범주형 분포 (Categorical Distribution)

그림 4.9 a) 여섯 개 범주에 대한 범주형 확률 분포. $\sum_{k=1}^6 \lambda_k = 1$ 조건을 만족하며, 예를 들어 편향된 주사위의 각 면이 나올 확률을 나타낼 수 있다. b) 해당 분포에서 무작위로 샘플링한 15개의 관측값 ${x_i}$. 각 범주 $k$가 등장한 횟수를 $N_k$라고 하면, $\sum_{k=1}^6 N_k = 15$이다.

두 번째 예제로, <이산 데이터> ${x_i}_{i=1}^I$에 대해 살펴본다. 

 

여기서 각 $x_i \in \{1, 2, \dots, 6\}$이며, 이는 편향된 주사위의 관측값일 수 있다 (그림 4.9 참조).

이러한 데이터를 설명하기 위해 범주형 분포(categorical distribution)를 사용한다. 

 

범주형 분포는 정규화된 히스토그램과 동일하며, 확률은 다음과 같이 정의된다:

 

$$Pr(x=k|λ_{1,...,6})=λ_k\tag{4.27}$$

 

여기서 $\lambda_k$는 범주 $k$가 나올 확률을 의미하며, 모든 $\lambda_k$는 0 이상이고 다음을 만족해야 한다:

 

$$\sum_{k=1}^6λ_k=1$$

 

4.5.1 최대 우도 추정 (Maximum Likelihood Estimation)

 

최대 우도 추정에서는 관측된 데이터에 대해 각 $\lambda_k$ 값을 피팅한다. 

 

목표는 전체 데이터에 대한 우도의 곱을 최대화하는 것이다:

 

$$\begin{align*} \hat{λ}_{1,...,6} &= \underset{λ_{1,...,6}}{\text{argmax}}\prod_{i=1}^IPr(x_i|λ_{1,...,6}) \\ &= \underset{λ_{1,...,6}}{\text{argmax}}\prod_{i=1}^6λ_k^{N_k} \end{align*}\tag{4.28}$$

 

여기서 각 $Pr(x_i \mid \lambda_1, \dots, \lambda_6)$는 범주형 분포의 확률 밀도이며, 

 

$N_k$는 학습 데이터에서 범주 $k$가 등장한 총 횟수이다.

 

우도를 직접 최적화하는 대신, 로그 우도를 최대화하는 것이 계산상 더 편리하다:

 

$$L=\sum_{k=1}^6N_k\log{λ_k}+ν\left ( \sum_{k=1}^6λ_k-1 \right )\tag{4.29}$$

 

두 번째 항은 제약 조건 $\sum \lambda_k = 1$을 만족시키기 위해 도입된 라그랑주 승수(Lagrange multiplier) $\nu$이다.

 

$L$을 각 $\lambda_k$와 $\nu$에 대해 미분하고 0으로 두면 다음을 얻는다:

 

$$\hat{λ}_k=\frac{N_k}{\sum_{m=1}^6N_m}\tag{4.30}$$

 

즉, 각 $\lambda_k$는 해당 범주가 나타난 비율과 동일하다.

이 결과는 직관적이며, 각 범주가 전체 데이터에서 차지하는 비율로 확률을 추정하는 것이다.

 

요약

• 범주형 분포는 이산 클래스에 대한 확률 분포로, 각 클래스의 상대적 등장 빈도로 모델링된다.
• ML 피팅은 각 범주의 상대 빈도를 그대로 확률 추정값으로 사용한다.
• 이는 모델에 사전 정보가 없을 때 가장 단순하면서도 직관적인 접근 방식이다.

4.5.2 최대 사후 확률 추정 (Maximum a Posteriori)

그림 4.10 a–e) $\alpha_1, \dots, \alpha_6 = 1$인 Dirichlet 사전 분포로부터 생성한 5개의 샘플. 이 경우 사전은 균등하며, 샘플은 무작위적이고 구조 없는 확률 분포를 보인다. f–j) 데이터로부터 갱신된 Dirichlet 사후 분포로부터 생성한 샘플. 이 분포는 3번 범주가 높고 4번 범주가 낮은 형태를 선호하며, 이는 학습 데이터의 패턴을 반영한다.

최대 사후 확률 추정(MAP)을 수행하기 위해서는 사전 분포를 정의해야 한다.

 

여기서는 Dirichlet 분포를 선택한다. 

 

이 분포는 범주형 우도(categorical likelihood)에 대한 켤레 사전(conjugate prior)이기 때문에 수학적으로 매우 편리하다.

Dirichlet 분포는 여섯 개의 범주형 파라미터 $\lambda_1, \dots, \lambda_6$에 대한 사전 분포이며, 

 

시각화는 어렵지만, 샘플을 통해 그 형태를 직관적으로 확인할 수 있다 (그림 4.10a–e 참고).

 

MAP 해는 다음과 같이 정의된다:

 

$$\begin{align*} \hat{λ}_{1,...,6} &= \underset{λ_{1,...,6}}{\text{argmax}}\left [ \prod_{i=1}^IPr(x_i|λ_{1,...,6})⋅Pr(λ_{1,...,6})\right ] \\ &= \underset{λ_{1,...,6}}{\text{argmax}}\prod_{i=1}^6λ_k^{N_k+α_k-1} \end{align*}\tag{4.31}$$

 

이때,

• $Pr(x_i \mid \lambda_1, \dots, \lambda_6)$는 범주형 우도 (Categorical likelihood),
• $Pr(\lambda_1, \dots, \lambda_6)$는 Dirichlet 사전 분포로, 다음과 같이 주어진다:

$$\hat{λ}_{1,...,6}=\frac{1}{Z}\prod_{i=1}^6λ_k^{α_k-1}$$

 

따라서 전체 목적 함수는 다음과 같이 정리된다:

 

$$\prod_{i=1}^6λ_k^{N_k+α_k-1}$$

 

여기서 $N_k$는 학습 데이터에서 범주 $k$가 등장한 횟수이다.

 

목적 함수는 라그랑주 승수를 사용해 $\sum_k \lambda_k = 1$ 조건을 만족시키면서 최적화된다.

 

이제 로그를 취한 후 미분하고 정리하면, 각 파라미터의 MAP 추정값은 다음과 같다:

 

$$\hat{λ}_k=\frac{N_k+α_k-1}{\sum_{m=1}^6(N_m+α_m-1)}\tag{4.32}$$

 

이는 범주 $k$의 등장 횟수 $N_k$와 사전의 하이퍼파라미터 $\alpha_k$가 결합된 형태이다.

 

즉, 데이터와 사전 정보가 결합된 가중 평균 형태로 해석할 수 있다.

특히, 모든 $\alpha_k = 1$로 설정하면 Dirichlet 분포는 균등 사전(uniform prior)이 되며,

 

이 경우 MAP 추정식은 최대 우도 해와 동일하게 된다 (식 4.30 참조).

 

4.5.3 베이지안 접근 (Bayesian Approach)

 

베이지안 접근에서는 데이터 ${x_i}_{i=1}^I$에 기반해 매개변수 $\lambda_1, \dots, \lambda_6$에 대한 사후 분포를 계산한다:

 

$$Pr(λ_{1,...,6}|x_{1,...,I})=\frac{\prod_{i=1}^IPr(x_i|λ_{1,...,6})⋅Pr(λ_{1,...,6})}{Pr(x_{1,...,I})}\tag{4.33}$$

 

기서 범주형 우도 $Pr(x_i \mid \lambda_1, \dots, \lambda_6)$는 범주형 분포(Categorical distribution)이며,

 

사전 분포는 Dirichlet 분포 $Dir_{\lambda_1,\dots,\lambda_6}[\alpha_1,\dots,\alpha_6]$로 설정된다.

켤레 사전 관계에 따라, 사후 분포는 Dirichlet 분포의 동일한 형태를 유지하며 파라미터만 다음과 같이 갱신된다:

 

$$\tilde{α}_k=N_k+α_k$$

 

즉, 사후 분포는 다음과 같이 표현된다:

 

$$Pr(λ_{1,...,6}|x_{1,...,I})=\text{Dir}_{λ_{1,...,6}}[\tilde{α}_{1,...,6}]$$

 

이러한 사후 분포로부터의 샘플은 앞서 Figure 4.10f–j에 시각화되어 있다.

 

예측 분포 (Predictive Density)

그림 4.11 a) $\alpha_1, \dots, \alpha_6 = 1$인 경우, ML과 MAP 예측 분포는 동일하며, 데이터의 상대 빈도와 정확히 일치한다. b) 베이지안 예측 분포는 더 완만한 형태를 가지며, 관측되지 않은 범주 ($x=4$)에도 작은 확률을 할당한다.

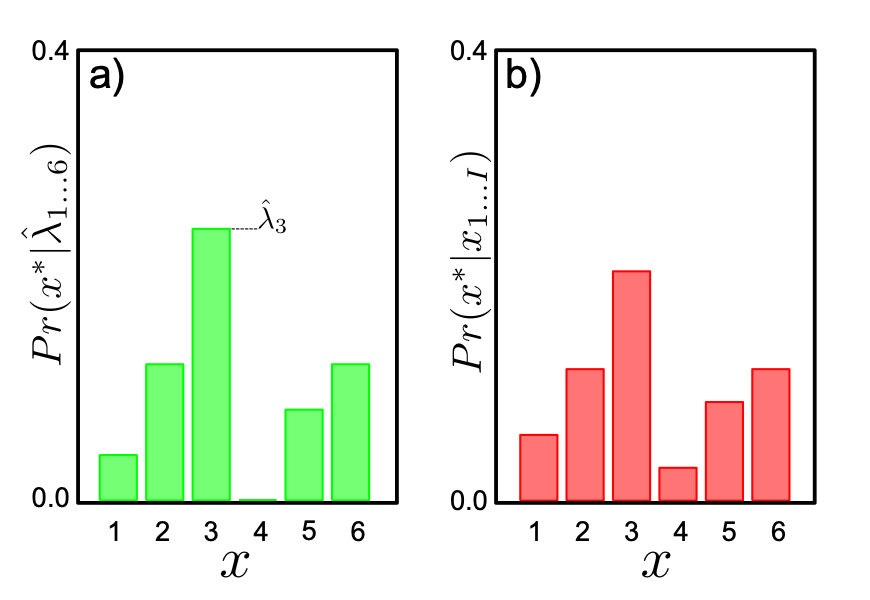
ML 및 MAP 추정에서는 추정된 파라미터를 사용해 새로운 데이터 $x^*$의 예측 확률을 계산한다.

 

즉, 단순히 범주형 분포의 확률 밀도 함수를 $\hat{\lambda}_k$로 평가한다.

특히 $\alpha_k = 1$ (균등 사전)일 때는, MAP과 ML이 동일한 결과를 제공하며, 

 

관측된 데이터의 상대 빈도와 정확히 일치한다 (그림 4.11a).

 

베이지안 접근에서는 모든 가능한 파라미터 조합에 대해 예측을 수행하고,

사후 분포로 가중 평균하여 예측 확률을 계산한다:

 

$$Pr(x^*|x_{1...I})=\int Pr(x^*|λ_{1,...,6})⋅Pr(λ_{1,...,6}|x_{1...I})dλ_{1,...,6}\tag{4.34}$$

 

 적분은 다시 Dirichlet–Categorical 관계를 활용하여 폐형식으로 계산 가능하다:

 

$$Pr(x^*=k|x_{1...I})=\frac{N_k+α_k}{\sum_{j=1}^6(N_j+α_j)}\tag{4.35}$$

 

즉, 예측 확률은 관측 빈도 $N_k$와 사전 하이퍼파라미터 $\alpha_k$의 합을 기반으로 정규화된다.

이 결과는 Figure 4.11b에 시각화되어 있다.

 

베이지안 예측의 특징

• 베이지안 예측은 항상 덜 확신에 찬(moderate) 분포를 생성한다.
• 관측되지 않은 범주에 대해서도 0이 아닌 확률을 부여한다.
  예: 15개의 샘플 중 $x=4$가 한 번도 등장하지 않았더라도, 베이지안 방식은 이에 작은 확률을 부여한다.
  
  

이는 “관측되지 않았다고 해서 불가능하다고 간주할 수 없다”는 원칙을 따르며,

 

미지의 가능성에 대해 열려 있는 베이지안 추론의 본질을 잘 보여준다.

 

요약

• 베이지안 접근은 사후 분포 전체를 고려한 예측을 수행하므로, 관측되지 않은 경우에도 확률을 부여한다.
• 이는 과도한 확신을 피하고 일반화 가능성을 확보하는 데 중요하다.
• 특히 데이터가 적을 때, 베이지안 추론은 과소적합이나 과적합을 방지하는 안전장치 역할을 수행한다.

4장 요약

 

이 장에서는 데이터에 확률 분포를 피팅하고, 새로운 데이터 포인트의 확률을 예측하는 세 가지 방법을 소개하였다.

 

세 가지 방법은 다음과 같다:

1. 최대 우도 추정 (Maximum Likelihood, ML)
2. 최대 사후 확률 추정 (Maximum A Posteriori, MAP)
3. 베이지안 접근 (Bayesian Approach)

이 중에서 가장 바람직한 방법은 베이지안 접근이다.

 

이 접근법에서는 불확실한 파라미터에 대해 단일한 점 추정(point estimate)을 찾을 필요가 없으며,

 

그로 인해 발생할 수 있는 추정 오차도 회피할 수 있다.

그러나 베이지안 접근은 켤레 사전(conjugate prior)이 존재할 때만 수학적으로 tractable(해석 가능)하다.

 

켤레 사전이 있으면:

• 파라미터에 대한 사후 분포 $Pr(\theta \mid x_1, \dots, x_I)$를 폐형식으로 계산할 수 있고,
• 예측 분포에서 요구되는 적분도 명확하게 계산할 수 있다.

반대로, 켤레 사전이 존재하지 않거나 계산이 복잡할 경우에는 일반적으로 MAP 추정에 의존하게 된다.

한편, 최대 우도 추정(ML)은 정보를 제공하지 않는 사전 분포(uninformative prior)를 가정한 

 

MAP 추정의 특수한 경우로 해석할 수 있다.

 

정리:

 

• 베이지안 접근은 이론적으로 가장 강력하지만, 계산 가능성은 켤레 사전의 존재 여부에 달려 있다.
• MAP 추정은 현실적인 대안으로 널리 쓰이며, ML 추정은 그 하위 개념이다.
• 단일 추정치가 아닌 확률 분포 자체를 유지한다는 점에서, 베이지안 방법은 추론의 정확성과 일반화 측면에서 우수하다.