티스토리 뷰
[Java]시간 복잡도(Time Complexity), 빅-오 표기법(Big-O Notation)
Vagabund.Gni 2022. 7. 28. 14:51목차
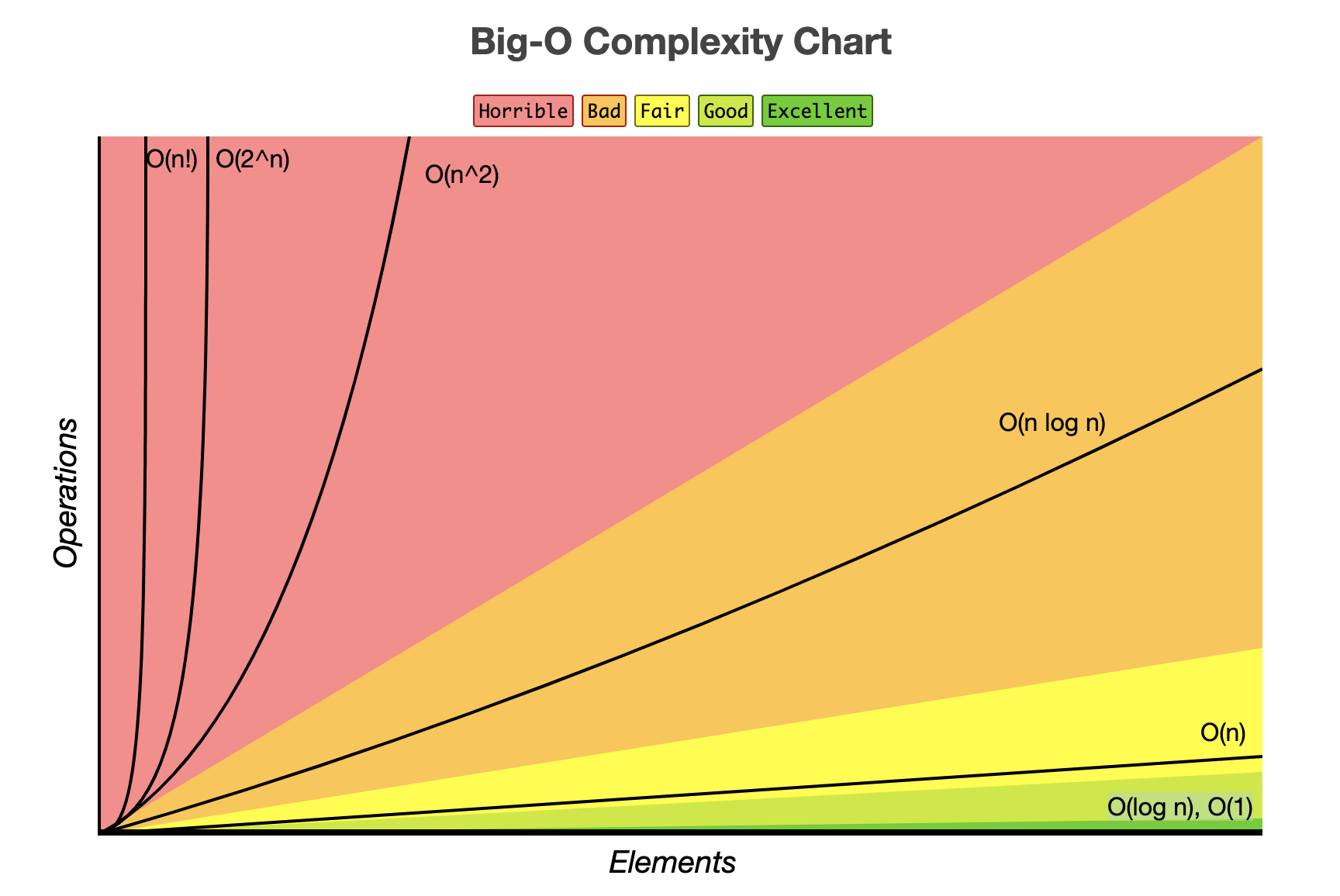
효율적인 알고리즘이란 입력값의 증가에 따른 시간의 비율을 최소화한 것이다.
따라서 효율적인 알고리즘을 고민한다는 것과 시간 복잡도를 낮춘다는 건 같은 말이 된다.
시간 복잡도란 '입력값과 연산 수행 시간의 상관관계를 나타내는 척도'이며, 쉽게 말하면 아래와 같다.
입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?
시간 복잡도를 표기하는 방법은 다음의 세 가지가 있으며,
- Big-O(빅-오) - 최악의 경우 고려
- Big-Ω(빅-오메가) - 최선의 경우 고려
- Bid-θ(빅-세타) - 중간(평균)의 경우 고려
언제나 최악의 경우를 고려하는 것이 바람직하기 때문에 빅-오 표기법이 많이 쓰인다.
O(f(n))과 같이 표시하며, 이는 입력값 n이 증가할 때 연산 횟수가 f(n)으로 증가한다는 뜻이다.
아래의 내용은 전부 빅-오 표기법에 대한 것이다.
O(1)
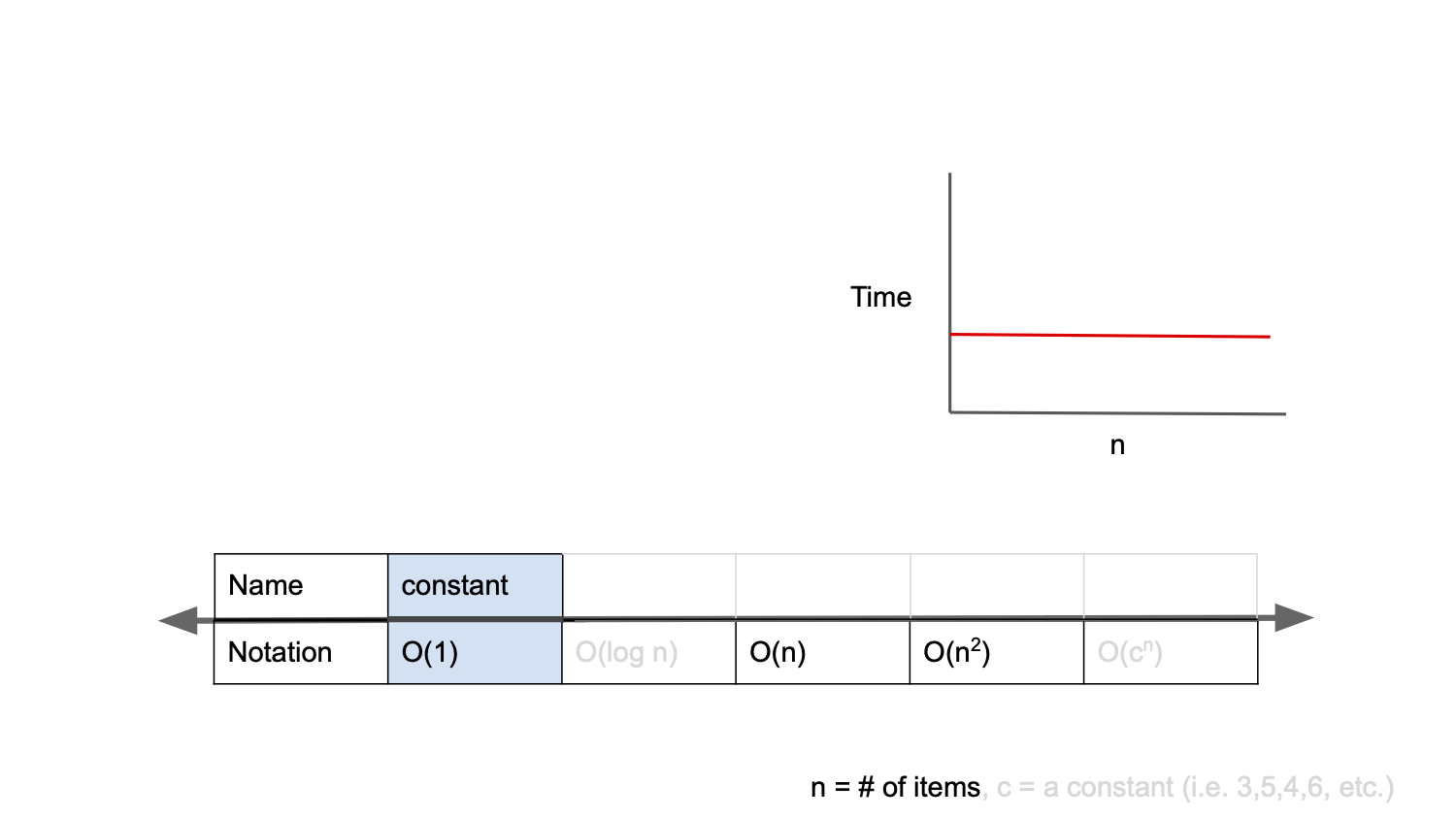
O(1)은 상수 복잡도(Constant Complexity)라 부르며, 입력값이 증가해도 연산 횟수가 변하지 않는다.
public int O_1_algorithm(int[] arr, int index) {
return arr[index];
}
int[] arr = new int[]{1,2,3,4,5};
int index = 1;
int results = O_1_algorithm(arr, index);
System.out.println(results);
// 출력 결과
2위 예시는 배열에서 원하는 인덱스의 값을 읽어오는 코드이다.
배열의 요소가 100만 개가 된다고 해도 인덱스만 알고 있다면 한 번의 연산으로 값을 얻을 수 있다.
O(n)
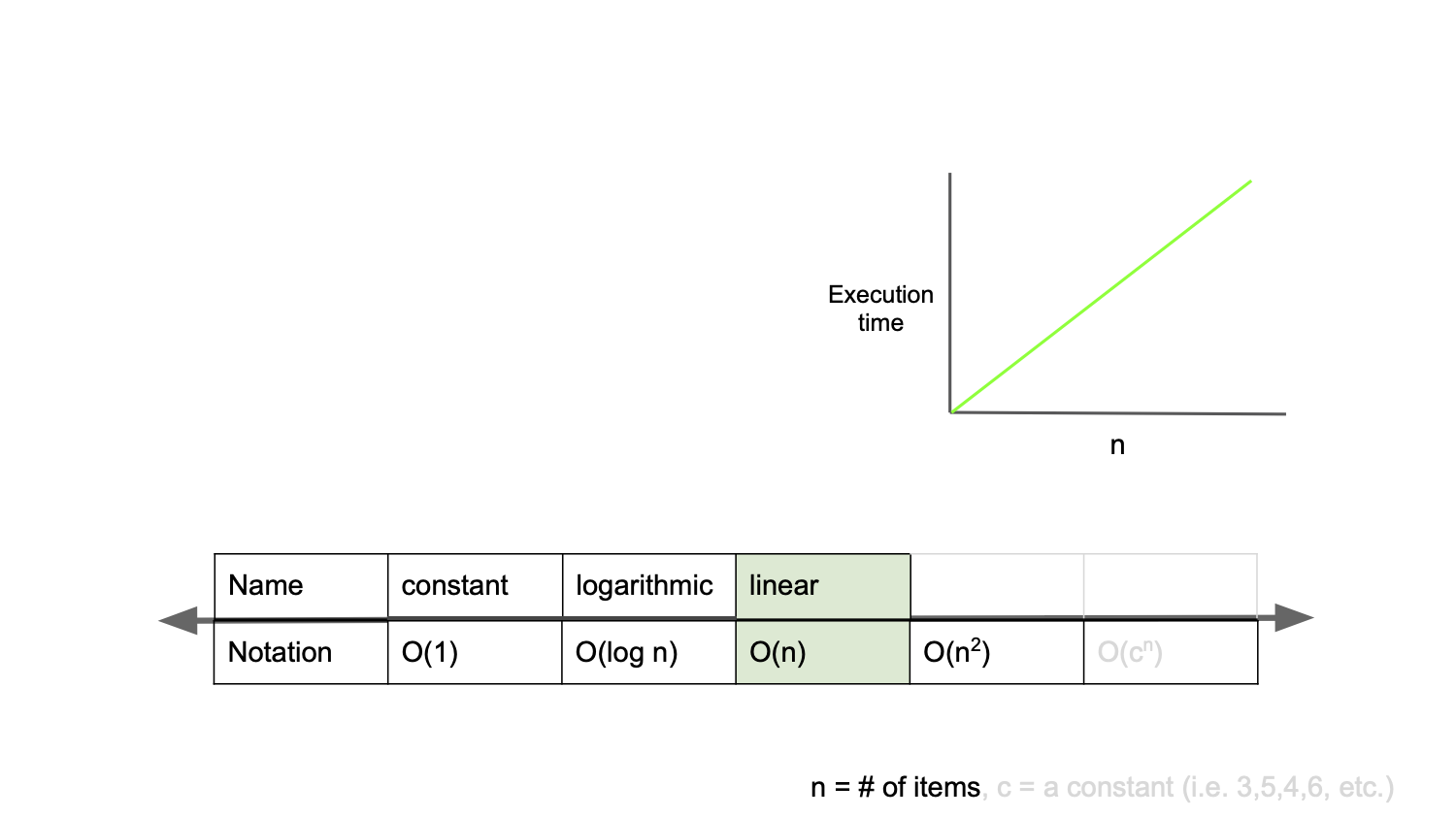
O(n)은 선형 복잡도(Linear Complexity)라고 불리며, 입력값과 연산 횟수가 비례해서 늘어나는 경우이다.
public void O_n_algorithm(int n) {
for(int i = 0; i < n; i++) {
// do something for 1 second
}
}
public void another_O_n_algorithm(int n) {
for(int i = 0; i < n * 2; i++) {
// do something for 1 second
}
}위의 메서드 들은 n이 두 배가 되면 연산 횟수도 두 배가 된다.
아래의 another_O_n_algorithm(int n) 메서드는 연산 결과가 2n으로 증가하지만
빅-오 표기법에선 최고차항의 차수만 보기 때문에 O(2n)이 아닌 O(n)으로 쓰며
이 원칙은 모든 복잡도에서 적용된다.(ex. O(n^3) -> O(n^2))
O($log(n)$)
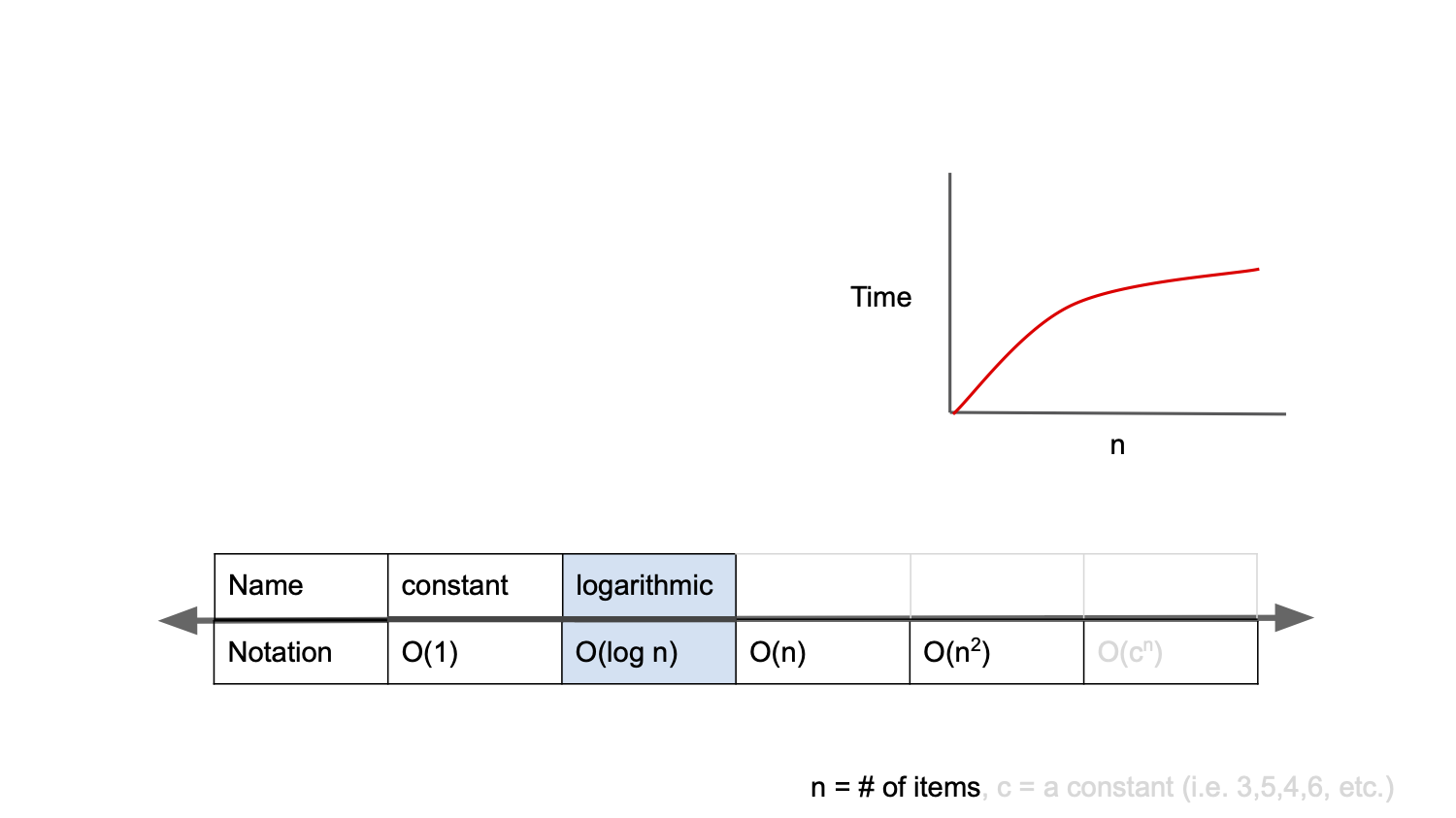
O(log n)은 로그 복잡도(Logarithmic Complexity)라 불리며 O(1) 다음으로 빠른 속도를 가진다.
이진 탐색 트리(BST - Binary Search Tree)에서 원하는 값을 선택할 때의 시간 복잡도라고 보면 된다.
O($n^{2}$)
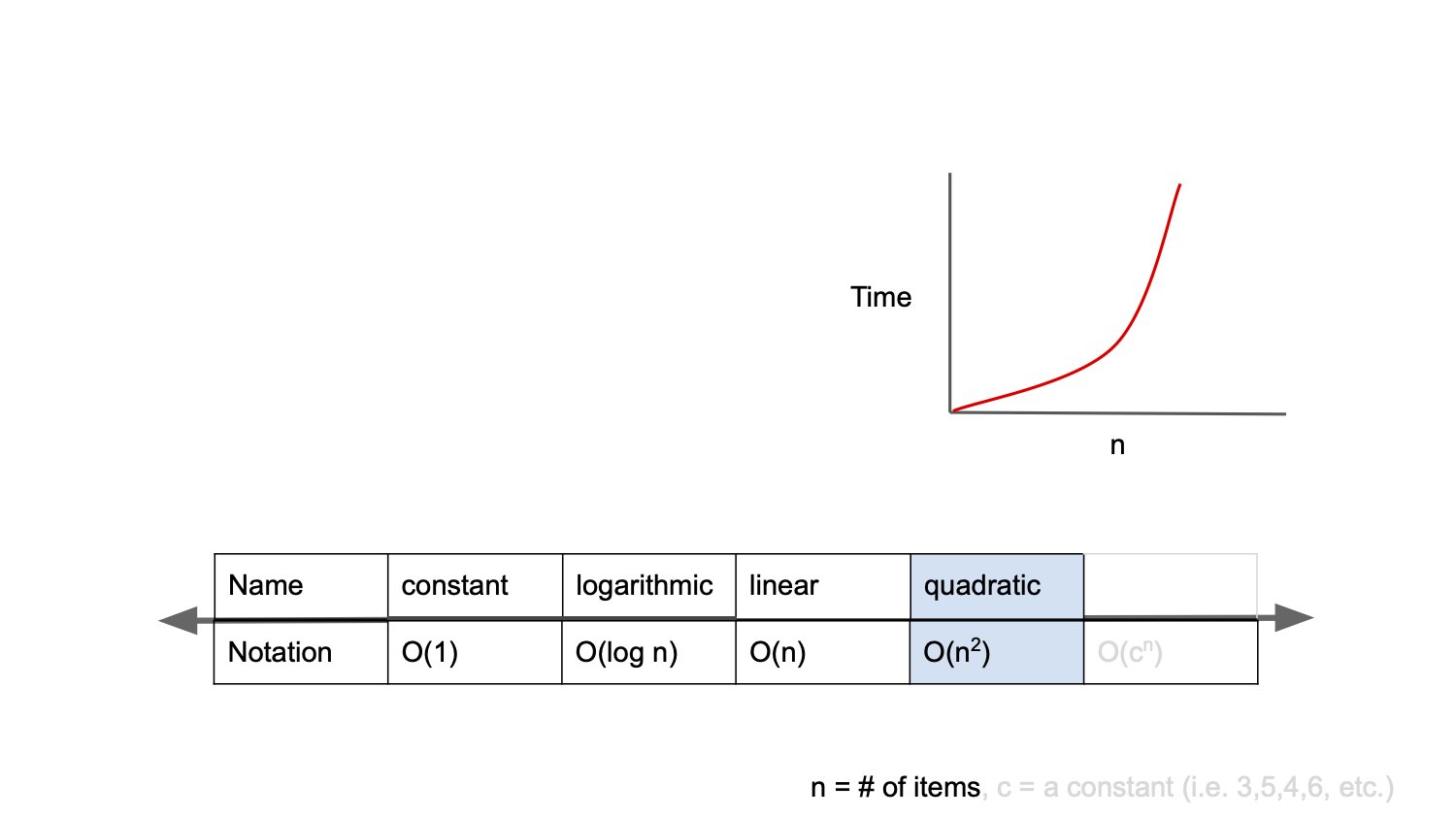
O(n^2)는 다차형 복잡도(Polynomial Complexity) 혹은 이차 복잡도(Quadratic Complexity)라고 불린다.
입력값이 10배 증가할 때 연산 횟수가 100배(10^2배) 증가하는 경우이다.
public void O_quadratic_algorithm(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
// do something for 1 second
}
}
}
public void another_O_quadratic_algorithm(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
for(int k = 0; k < n; k++) {
// do something for 1 second
}
}
}아래의 메서드는 O(n^3)의 복잡도를 가졌지만 O(n^2)로 표기한다.
O($2^{n}$)
O(2^n)은 지수형 복잡도(Exponential Complexity)라고 불린다.
메모이제이션(Memoization)이 되어있지 않은 재귀 함수가 이 경우에 해당하며, 다차 형태와 모양은 비슷해도 엄청난 차이가 난다.
구현한 알고리즘이 이 복잡도를 가지고 있다면 다시 생각해보는 것이 좋다.
public int fibonacci(int n) {
if(n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci (n - 2);
}}
속도 차이
가장 위에서 봤던 그래프를 다시 보자
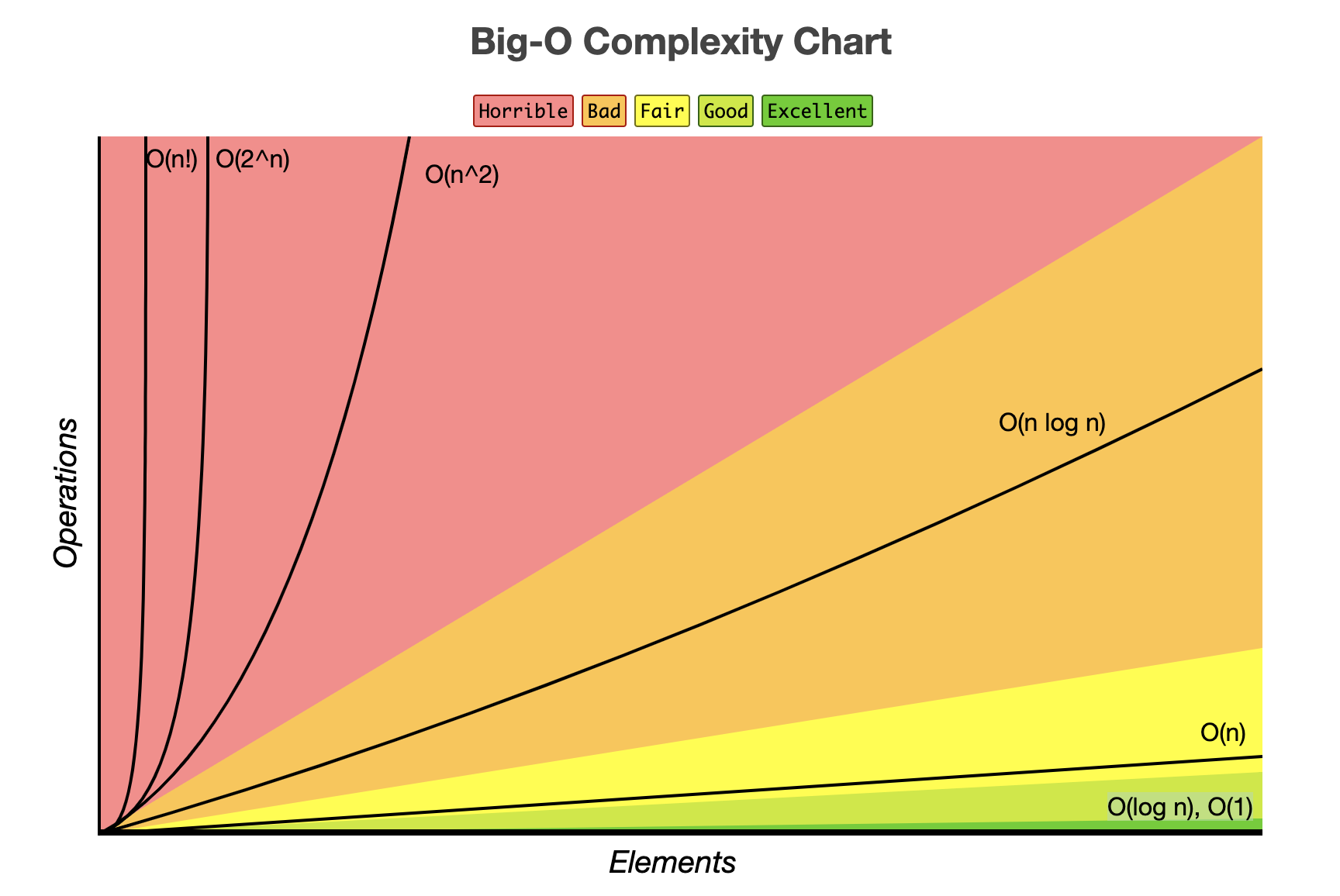
n의 값이 증가함에 따라 복잡도별 연산 횟수가 얼마나 차이 나는지 확인할 수 있다.
구체적으로 숫자를 들면 아래와 같다.
| 복잡도 | 1 | 10 | 100 |
| O(1) | 1 | 1 | 1 |
| O(log n) | 0 | 2 | 5 |
| O(n) | 1 | 10 | 100 |
| O(n log n) | 0 | 20 | 461 |
| O(n^2) | 1 | 100 | 10000 |
| O(2^n) | 1 | 1024 | 1267650600228229401496703205376 |
| O(n!) | 1 | 3628800 | ~9.332621544×10^(157) |
그렇다고 복잡도가 아래로 내려갈 수록 꼭 느려지기만 하는 것은 아닌데,
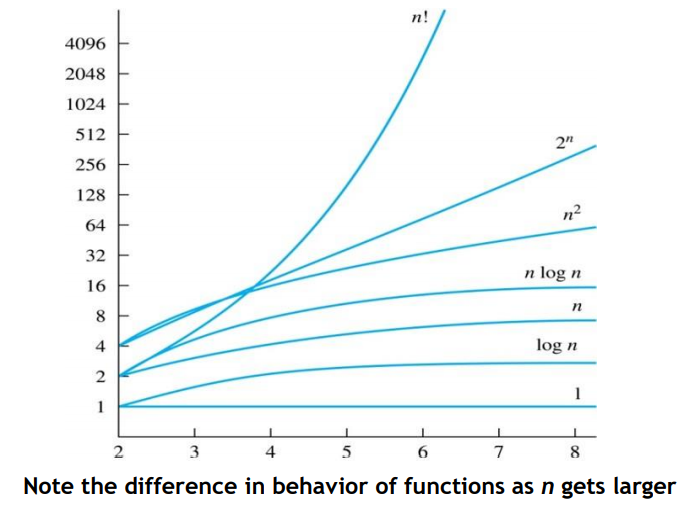
출처: https://velog.io/@seyeop03/Chapter-3.2-Growth-of-Functions
적당히 작은 수에선 순위가 뒤집히기도 한다는 것을 알 수 있다.
이 속도 차이를 이용해 코딩 테스트시 시간제한과 데이터 크기에 따라 복잡도를 예상해볼 수 있는데,
대략 다음과 같다.
| 데이터 크기 | 예상 시간 복잡도 |
| n ≤ 1,000,000 | O(n) or O (log n) |
| n ≤ 10,000 | O() |
| n ≤ 500 | O() |
'Java+Spring > Java' 카테고리의 다른 글
| [Java]유클리드 호제법, 최대공약수, 최소공배수 (0) | 2022.07.31 |
|---|---|
| [Java]String, int 배열의 정렬 (0) | 2022.07.29 |
| [Java]완전 탐색(Exhaustive Search, Brute-Force Algorithm) (0) | 2022.07.28 |
| [Java]자료구조 - Graph (0) | 2022.07.27 |
| [Java]자료구조 - Tree (0) | 2022.07.26 |
| [Java]자료구조 - Queue (0) | 2022.07.25 |
- Total
- Today
- Yesterday
- 유럽여행
- Python
- 세계일주
- 알고리즘
- 리스트
- a6000
- 스프링
- 스트림
- 세계여행
- 남미
- spring
- 맛집
- Backjoon
- java
- 동적계획법
- 칼이사
- 세모
- RX100M5
- Algorithm
- 백준
- 여행
- 지지
- 기술면접
- 야경
- BOJ
- 중남미
- 유럽
- 면접 준비
- 파이썬
- 자바
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |

