티스토리 뷰
[Java]완전 탐색(Exhaustive Search, Brute-Force Algorithm)
Vagabund.Gni 2022. 7. 28. 22:00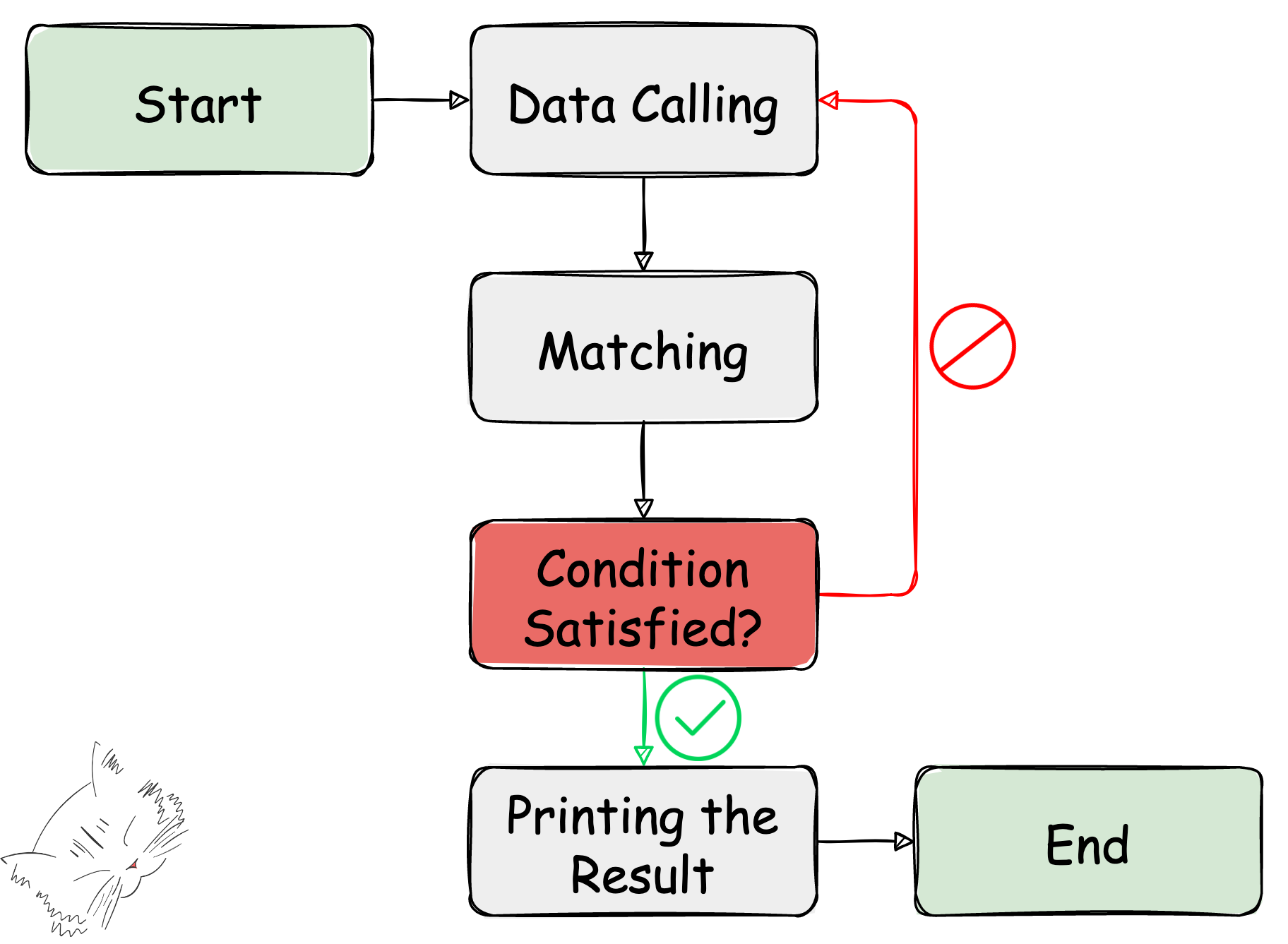
완전 탐색이란 컴퓨터의 성능을 믿고 모든 경우의 수를 다 체크하는 방법이다.
상대적으로 구현이 간단하고, 해가 존재한다면 반드시 찾을 수 있는 방법이기도 하다.
예를 들어 숫자 4자리로 구성된 자물쇠의 암호를 푼다면, '0000'부터 '9999'까지 다 넣어보는 방식이다.
당연하게도 최적의 솔루션을 제공해주지 않으며, 때문에 다음 두 상황에 주로 쓰인다.
- 적용 가능한 다른 알고리즘이 없을 때
- 복수의 솔루션을 확인해야 할 때
예를 들어 책 한 권이 주어지고 그 책에서 '고양이'라는 단어를 찾아야 한다고 가정해보자.
책은 당연하게도 단어들이 정렬되어 있지 않으므로 처음부터 끝까지 단어를 비교하는 수밖에 없다.
이럴 때 사용되는 것이 완전 탐색 알고리즘이며, 이 경우 시간 복잡도는 O(n)이다.
계속해서 완전 탐색의 활용에 대해 알아보자.
순차 검색 알고리즘(Sequantial Search)
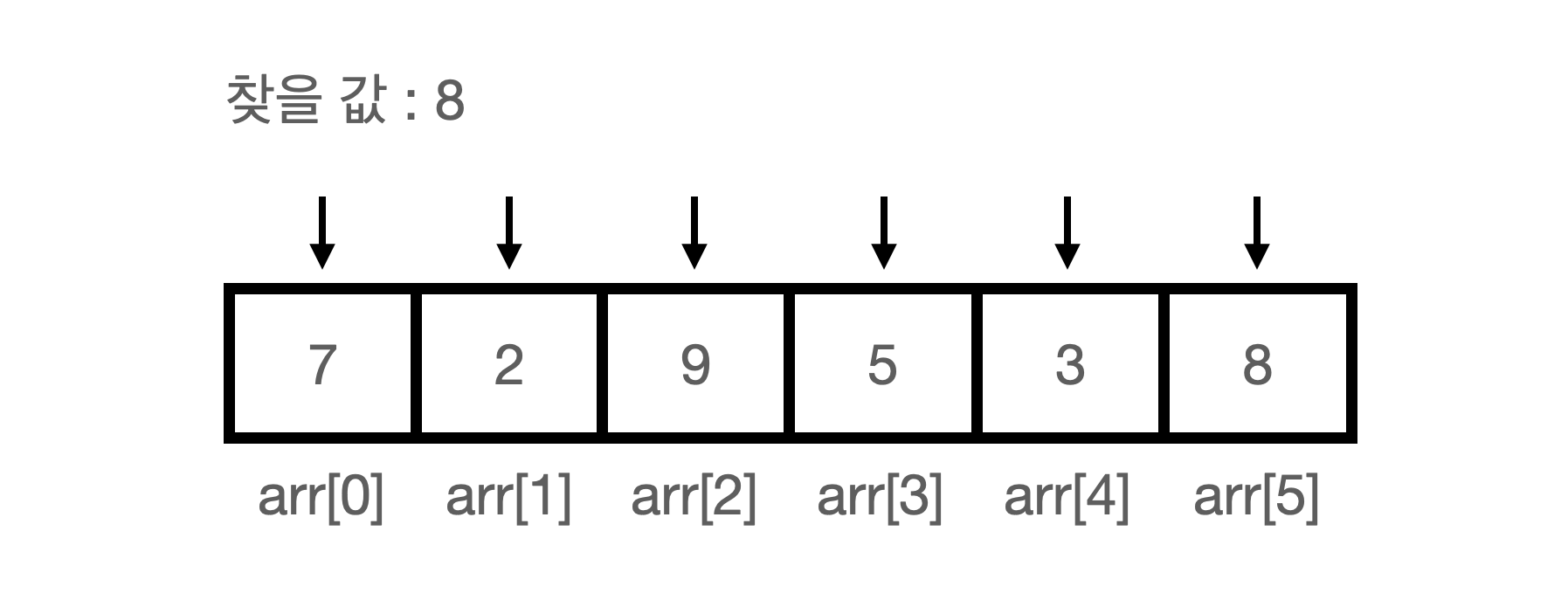
순차 검색 알고리즘은 첫 인덱스부터 마지막 인덱스까지 차례대로 검색하는 방법이다.
다음과 같이 구현한다.
public static boolean SequentialSearch2(int[]arr, int K) {
// 검색 키 K를 사용하여 순차 검색을 구현
// 입력: n개의 요소를 갖는 배열 arr와 검색 키 K
// 출력: boolean result
int n = arr.length;
// 결과를 저장할 boolean result선언, 초기값은 false
boolean result = false;
for(int i = 0; i < n; i++) { // 현재의 배열 개수를 n에 할당
if(arr[i] == K) result = true;
}
// 출력: K값과 같은 요소 인덱스 또는 요소가 없을 때 false
return result;
}
//배열을 순회하는 도중에, 해당하는 값이 발견되더라도 배열을 모두 순회한 이후에 결과값을 리턴
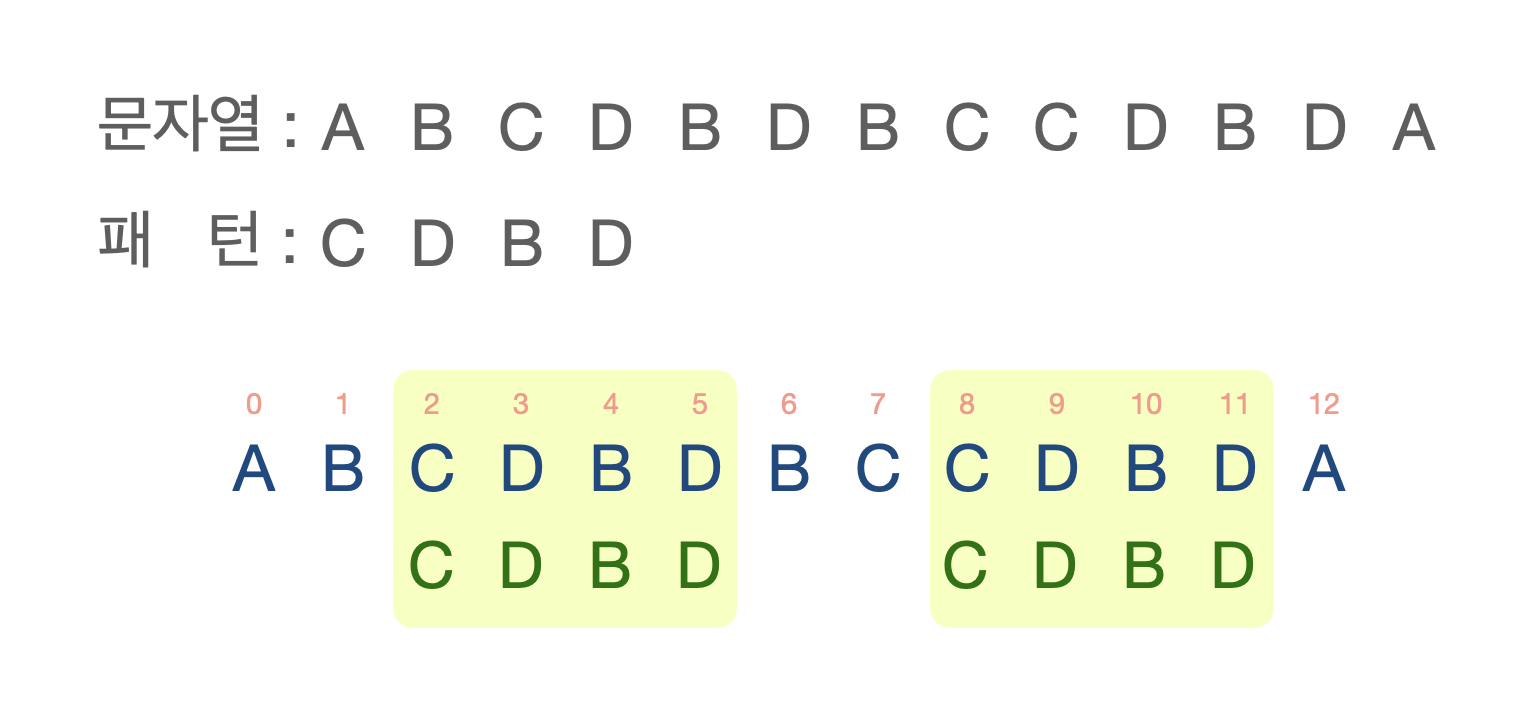
문자열 매칭 알고리즘(Brute-Force String Matching)
길이가 n인 문자열이 길이가 m인 문자열 패턴을 포함하는지 탐색
public static boolean BruteForceStringMatch(int[]arr, int[]patternArr) {
// 입력: 길이 n의 정수 배열 arr, 길이 m의 정수 패턴 배열 patternArr
// 출력: boolean
int n = arr.length;
int m = patternArr.length;
// 전체 문자열 길이 n에서 패턴의 길이 m을 뺀 만큼 반복
// i 반복문은 패턴과 비교의 위치를 잡는 반복문
for(int i = 0; i < n - m; i++) {
//j는 전체와 패턴의 요소 하나하나를 비교하는 반복문
int j = 0;
// j가 패턴의 길이보다 커지면 안되기때문에 길이만큼만 반복
// 패턴에서는 j인덱스와 전체에서는 i + j 인덱스의 값이 같은지 확인
// 같을때 j에 +1
while(j < m && patternArr[j] == arr[i + j]) {
j = j + 1;
}
// j와 패턴 수가 같다는 것은 패턴의 문자열과 완전히 같은 부분이 존재한다는 의미
if(j == m) {
return true;
}
}
return false;이 알고리즘의 시간 복잡도는 O(nm)이다.
선택 정렬 알고리즘(Selection sort)
배열이 완전한 오름차순, 혹은 내림차순에 이를 때까지 기준에 맞춰 요소를 교환하는 알고리즘이다.

출처: https://github.com/GimunLee
GimunLee - Overview
🏃♂️ Practice makes perfect. GimunLee has 39 repositories available. Follow their code on GitHub.
github.com

public static int[] SelectionSort(int[]arr) {
// 입력: 정렬 가능한 배열 arr
// 출력: 오름차순으로 정렬된 배열
for(int i = 0; i < arr.length - 1; i++) {
// 배열의 0번째 인덱스부터 마지막 인덱스 직전까지 반복
int min = i;
// 현재 인덱스를 최소값의 인덱스를 나타내는 변수에 할당
for(int j = i + 1; j < arr.length; j++) {
// i + 1번째 인덱스부터 끝까지 비교
if(arr[j] < arr[min]) {
// j인덱스의 배열 값이 현재 인덱스의 배열 값보다 작다면
min = j;
// j를 최소값을 나타내는 인덱스로 할당
}
}
// 반복문을 끝까지 돌면 min에는 최소값의 인덱스가 있음
// temp를 이용해 i와 min의 자리 변경
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
// 모든 반복문이 끝나고 정렬 완료된 배열 반환
return arr;
}이 경우의 시간 복잡도는 O(n^2)이다.
순열(Permutation)
순열은 서로 다른 n개의 원소에서 r개를 중복 없이, 순서에 상관있게 뽑아 나열하는 것이다.
nPr의 형태로 자주 표현되며, 그 경우의 수는 아래와 같다.

순열은 탐색할 때 재귀 함수로 표현하는 것이 편한데, 이 경우 해당 인덱스의 숫자가 사용 중인지 판단하는 배열이 따로 필요하다.
이미 뽑은 숫자라면 넘어가야 하기 때문이다.
import java.util.Arrays;
public class BruteForce4 {
public static void main(String[] args) {
n = 5;
numbers = new int[n];
isSelected = new boolean[n+1];
Permutation(0);
System.out.println("순열의 개수: " + count);
}
static int n; // 원소 개수
static int[] numbers; // 순열을 저장할 배열
static boolean[] isSelected; // 뽑았는지 여부를 저장할 배열
static int count; // 순열 개수
public static void Permutation(int k) {
// base condition
if(k == n) {
count++;
System.out.println(Arrays.toString(numbers));
return;
}
for(int i = 1; i <= n; i++) {
if (isSelected[i]) continue; // 중복 검사
// 중복이 아니라면
numbers[k] = i;
isSelected[i] = true;
Permutation(k + 1); // 다음 요소 뽑기
isSelected[i] = false;
}
}
}1부터 n까지의 숫자로 순열을 만드는 코드이다.
'Java+Spring > Java' 카테고리의 다른 글
| [Java]멱집합(Power Set) (1) | 2022.08.01 |
|---|---|
| [Java]유클리드 호제법, 최대공약수, 최소공배수 (0) | 2022.07.31 |
| [Java]String, int 배열의 정렬 (0) | 2022.07.29 |
| [Java]시간 복잡도(Time Complexity), 빅-오 표기법(Big-O Notation) (0) | 2022.07.28 |
| [Java]자료구조 - Graph (0) | 2022.07.27 |
| [Java]자료구조 - Tree (0) | 2022.07.26 |
- Total
- Today
- Yesterday
- 세계일주
- a6000
- 남미
- spring
- 유럽
- 맛집
- 리스트
- 파이썬
- 유럽여행
- 백준
- 세모
- BOJ
- Algorithm
- java
- Python
- RX100M5
- 기술면접
- 스트림
- 중남미
- Backjoon
- 여행
- 자바
- 면접 준비
- 지지
- 칼이사
- 스프링
- 야경
- 알고리즘
- 세계여행
- 동적계획법
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
