티스토리 뷰
[Java+Python]11049번, 행렬 곱셈 순서
Vagabund.Gni 2023. 7. 10. 15:45목차
문제
크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다.
행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.
예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해 보자.
- AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
- BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오.
입력으로 주어진 행렬의 순서를 바꾸면 안 된다.
입력
첫째 줄에 행렬의 개수 N(1 ≤ N ≤ 500)이 주어진다.
둘째 줄부터 N개 줄에는 행렬의 크기 r과 c가 주어진다. (1 ≤ r, c ≤ 500)
항상 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.
출력
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다.
정답은 $2^{31}-1$ 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 $2^{31}-1$보다 작거나 같다.
풀이
뜬금없지만 행렬 곱셈은 교환법칙이 성립하지 않는다.
때문에 곱하는 행렬의 순서를 마음대로 바꾸는 것은 가능하지 않으며, 문제에서도 이를 감안해 금지한 것 같다.
지난번 피보나치수열을 행렬의 거듭제곱으로 표현할 때도 그렇고,
이렇게 행렬의 특성을 되짚어보니 대학원에 돌아온 것 같기도 하고 괜히 그렇다.
하여간에 이 문제는, 행렬 체인 곱셈(Matrix Chain Multiplication)에서 연산의 최솟값을 구하는 문제이다.
결합법칙이 성립하는 행렬 곱셈의 성질을 이용해서, 다수의 행렬을 곱할 때 가장 작은 연산의 수를 구하는 것이라고 할 수 있다.
문제에 대한 설명은 위의 <문제> 파트에 쓰여있으니, 여기서는 문제를 푸는 알고리즘에 대해 간결하게 설명한다.
먼저 이 문제는, 지난번 문제와는 다르게 누적합이나 누적곱 등의 테크닉을 사용할 수 없다.
순수하게 DP만을 사용해서 문제를 풀어야 한다는 뜻인데, 조금 생각해 보면 오히려 좋다(?).
설명은 자바 코드를 가지고 진행한다. 내 알고리즘에서 파이썬은 그저 자바 코드의 번역이기 때문에 그렇다.
public class prob11049 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[n][2];
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
arr[i][0] = Integer.parseInt(st.nextToken());
arr[i][1] = Integer.parseInt(st.nextToken());
}먼저 행렬의 개수 n을 입력받아 각 행렬의 정보를 저장할 arr과 메모이제이션을 위한 dp[][]를 초기화한다.
for (int i = 1; i < n; i++) {
for (int j = 0; j < n - i; j++) {
int k = i + j;
dp[j][k] = Integer.MAX_VALUE;
for (int l = j; l < k; l++) {
int cost = dp[j][l] + dp[l + 1][k] + arr[j][0] * arr[l][1] * arr[k][1];
dp[j][k] = Math.min(dp[j][k], cost);
}
}
}여기서 각 인덱스의 의미는 아래와 같다.
- i: 현재 행렬 체인의 길이. 1부터 시작해서 n까지 증가하며 dp 테이블을 채운다.
- j: 현재 행렬 체인의 시작지점
- k: 현재 행렬 체인의 끝 지점. i + j로 계산된다.
- l: 행렬 체인을 두 부분으로 나누는 지점. j부터 k까지 증가하며 둘로 나눈 부분의 최소 연산 횟수를 계산한 뒤 dp를 갱신한다.
조금 더 풀어서 말로 설명하기 위해, i = 4, j = 2인 경우에 대해 생각하면 아래와 같이 진행된다.
- 체인의 길이(i)가 4, 시작점(j)이 2 이므로 현재 계산하는 행렬 체인은 2, 3, 4, 5번 행렬의 곱이다.
- 해당 행렬 체인을 l을 사용해 분할하며 계산한다. 가능한 모든 분할 지점을 고려하게 된다.
- 이때 dp[j][l], dp[l + i][k]는 분할지점을 기준으로 양 쪽의 부분 체인을 곱하는데 필요한 최소 연산 횟수이다.
해당 값들은 이전 반복에서 이미 계산되어 dp에 저장되어 있다. - arr[j][0] * arr[l][1] * arr[k][1]은 분할된 두 체인을 합치는데 드는 연산 횟수이다.
- 이렇게 구한 비용을 dp[j][k]와 비교하여 작은 쪽으로 갱신하며, 마지막엔 최소 연산 횟수가 저장된다.
System.out.println(dp[0][n - 1]);
}
}이어서 출력하면 끝이다.
행렬의 성질과 체인곱, 그리고 DP에 익숙하다면 그다지 어려운 문제는 아닌 것 같다.
Java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class prob11049 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[n][2];
int[][] dp = new int[n][n];
for (int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
arr[i][0] = Integer.parseInt(st.nextToken());
arr[i][1] = Integer.parseInt(st.nextToken());
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < n - i; j++) {
int k = i + j;
dp[j][k] = Integer.MAX_VALUE;
for (int l = j; l < k; l++) {
int cost = dp[j][l] + dp[l + 1][k] + arr[j][0] * arr[l][1] * arr[k][1];
dp[j][k] = Math.min(dp[j][k], cost);
}
}
}
System.out.println(dp[0][n - 1]);
}
}
Python
import sys
n = int(sys.stdin.readline().rstrip())
lst = [list(map(int, sys.stdin.readline().split())) for _ in range(n)]
dp = [[0 for _ in range(n)] for _ in range(n)]
for i in range(1, n):
for j in range(n - i):
k = i + j
dp[j][k] = float("inf")
for l in range(j, k):
cost = dp[j][l] + dp[l + 1][k] + lst[j][0] * lst[l][1] * lst[k][1]
dp[j][k] = min(dp[j][k], cost)
print(dp[0][n - 1])
Performance
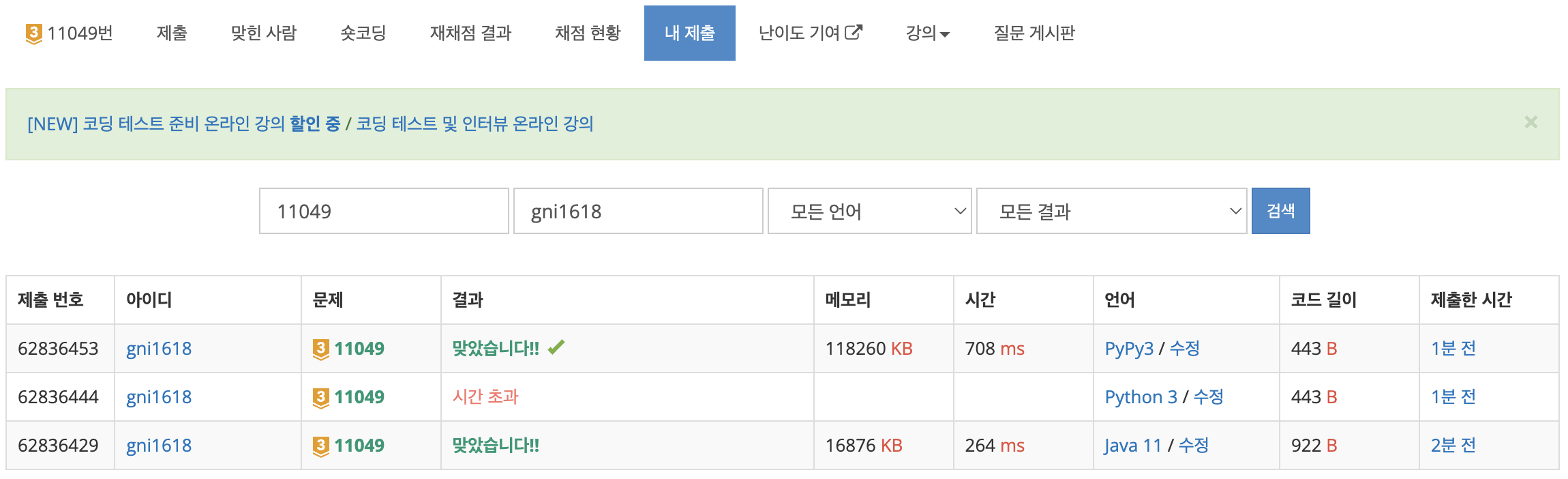
삼중 반복문이 나온 시점에서 파이썬으로는 어림도 없겠다 추측했지만 어림도 없었다.
PyPy3으로 해도 저 어마어마한 메모리...
반복문을 재귀함수로 바꾼다고 해도 깊이는 달라지지 않으므로 유의미할 것 같지는 않다.
이중을 초과하는 반복문은 그냥 PyPy3으로 돌리는 게 답인지도 모르겠다.
'Algorithm > [Java+Python+JavaScript]BackJoon' 카테고리의 다른 글
| [Java+Python]2629번, 양팔저울 (0) | 2023.07.14 |
|---|---|
| [JavaScript]2941번, 크로아티아 알파벳, 좀 더 어려운 문자열 다루기 (1) | 2023.07.12 |
| [Java+Python]1520번, 내리막길, DP+DFS (0) | 2023.07.12 |
| [JavaScript]2675번, 문자열 반복, 오버헤드 (0) | 2023.07.08 |
| [Java+Python]11286번, 절댓값 힙, Comparator (0) | 2023.07.04 |
| [JavaScript]3052번, 나머지, 배열에서 중복 제거, Set (0) | 2023.07.04 |
- Total
- Today
- Yesterday
- 세모
- 면접 준비
- 백준
- 스프링
- 알고리즘
- Python
- java
- 기술면접
- 동적계획법
- 유럽
- RX100M5
- 중남미
- 야경
- 리스트
- a6000
- 칼이사
- 남미
- spring
- 맛집
- 자바
- 여행
- Backjoon
- 세계여행
- 세계일주
- 유럽여행
- 지지
- BOJ
- Algorithm
- 스트림
- 파이썬
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |

