티스토리 뷰
[MSA+DDD]DDD는 MSA의 최적 모듈화를 찾는데 도움을 주는가?(10.1109/ACCESS.2021.3060895)
Vagabund.Gni 2023. 4. 22. 18:21목차
https://ieeexplore.ieee.org/document/9359794
Does Domain-Driven Design Lead to Finding the Optimal Modularity of a Microservice?
Information systems are moving into the cloud. The new requirements enforced by cloud standards are high availability, high scalability, and a reduced mean time to recovery. Due to these new requirements, information system architecture styles are also evo
ieeexplore.ieee.org
DDD에 대한 이론적인 부분이 궁금해서 찾다가 발견한 논문이다.
(내게 있어) 새로운 단어가 몇 개 등장해서, 단어 공부를 먼저 하고 시작.
Terminology
- DDD(Domain-Driven Design)
정해진 도메인을 중심으로, 각 도메인에 대한 깊은 이해를 바탕으로 소프트웨어를 설계하는 개발 방법론이다.
도메인에 대한 정확한 요구를 바탕으로 한 일관성 있는 구현을 통해 빠른 요구사항 반영과 쉬운 유지보수, 좋은 확장성을 자랑하며
객체지향적인 기술을 사용하여 구축한다. - SOA(Service Oriented Architecture)
직역하면 서비스 기반 (시스템) 아키텍처가 된다. 기존의 모놀리식 아키텍처를 서비스 단위로 분리해 모듈화 하고,
각 서비스를 독집적으로 개발하고 배포하며, 서비스 간의 통신은 별도의 미들웨어를 사용한다. - MSA(Microservice Architecture)
서비스를 더 작은 마이크로서비스로 분해하는 시스템 아키텍처 패턴이다.
SOA와 마찬가지로 각 서비스는 독립적으로 개발 및 배포가 가능하며, 마이크로서비스 간 통신은 보통 API를 사용한다. - Granularity
직역하면 낟알, 세분성 정도가 된다. 병렬 컴퓨팅의 맥락에선 '세분화 정도', 또는 '디테일 정도'가 되며,
위키백과에 의하면 연산과 통신의 비율, 그러니까 연산량 대비 통신의 양을 의미한다고 한다.
그러니까 결국 마이크로서비스가 얼마나 작은 단위로 나뉘어 있는가를 의미한다고 보면 된다. - Cohesion
역시 직역하면 응집도 정도가 된다. 물리 공부할 때 자주 보던 단어인 것 같기도..
MSA로 분할된 서비스는 각 서비스 간의 결합도는 약하되 모듈 내부의 응집도는 높아야 한다. - Bounded Context
이 용어는 DDD에서 사용되는 용어로, 직역하면 경계가 정해진 문맥, 혹은 영역을 가리킨다.
앱 내부에서 도메인의 경계를 정의하고, 경계 내에서 용어와 그 개념을 정확히 정의하는 것을 중요사항으로 친다.
DDD는 결국 이렇게 경계가 정해진 Bounded Context 사이의 상호작용으로 이루어져 있다고 봐도 되며,
각 Bounded Context는 서로 독립적인 설계, 개발 및 배포가 가능해야 한다. - Assembly
직역하면 조립품 정도가 된다.
여러 가지 의미가 있을 수 있지만 이 논문의 맥락에선 클래스를 기능에 따라 조립해 구성한 코드 단위를 가리킨다.
혹은 위에 적은 Bounded Context 수준에서의 클래스의 조합이며, 따라서 도메인과 비슷한 의미를 가진다. - Efferent Coupling
직역하면 입력 결합 정도가 된다.
특정 모듈의 객체(클래스, 메서드)가 다른 모듈의 객체를 얼마나 자주 호출하는지를 나타내는 지표이다.
즉, 해당 모듈이 다른 모듈에 얼마나 의존성을 가지는가를 측정할 수 있는 지표이며, 물론 높을수록 의존도가 높다.
MSA를 포함한 객체 지향 프로그래밍에서는 이 지표를 낮추며 응집도를 높이는 것을 목표로 하는데,
이는 낮은 의존성과 높은 응집도가 시스템의 유연성과 확장도를 보장하기 때문이다. - Afferent Coupling
직역하면 출력 결합, 혹은 송출 결합이 된다.
Efferent Coupling과는 반대로 해당 객체가 다른 객체에게 얼마나 많이 호출되는지를 나타낸다.
즉, 특정 모듈이 해당 모듈에 얼마나 의존성을 가지는가를 나타내는 지표이며, 마찬가지로 높을수록 의존도가 높다.
위와 같은 이유로 낮을수록 좋다. - AHP(Analytic Hierarchy Process)
한국어로는 분석적 계층과정이라고 한다.
의사결정 방법론 중 하나로, 여러 기준 간의 상대적 중요도를 계산한 뒤 이를 바탕으로 의사결정의 우선순위를 결정한다.
보통 수학을 사용해 정량적으로 측정되기 때문에, 정확한 의사결정에 도움이 된다. - LGMs, MGMs
논문에서 만들어 사용하는 약어로 각각 Less Granular Microservices, More Granular Microservices를 가리킨다.
이름에서 볼 수 있듯이 기본적인 실험 모델에 비해 적은 세분화와 많은 세분화를 구현한 모델이라는 뜻이다.
단어 공부가 끝났으니 본격적으로 논문의 질문과 결과에 대해 알아보자.
가독성을 위해 이번에는 초록과 결론을 먼저 알아보고, 중간 결과를 그 이후에 적는다.
Abstract
정보 시스템은 클라우드로 이동하고 있으며, 이 새로운 표준은 고가용성, 확장성, 줄어든 복구 시간을 요구한다.
이에 맞춰 진화한 모듈화 아키텍처 스타일의 사실상의 표준이 MSA이며, 그 소개 이래로 세분화 정도를 선택하는
방법은 현재 진행형으로 논쟁거리이다.
이 연구에서는 결합도와 응집도를 기반으로 MSA의 세분화 정도의 최적값을 조사한다.
또한 이연구는 이전 연구에서 DDD를 기반으로 MSA를 제안한 두 가지 모델을 기반으로 한다.
각 예제는 더 많이, 그리고 더 적게 세분화된 모델로 수정되었으며, 기존 모델과 결합도 및 응집도를 비교한다.
우리는 DDD가 모듈화 된 MSA를 찾는데 좋은 결과를 제공한다는 것을 관찰할 수 있었다.
Conclusion
이 연구의 목적은 MSA에서 최적화된 Bounded Context와 세분화도를 찾는 것이었다.
이를 위해 두 개의 DDD-driven 애플리케이션을 선택해 각각 MGM으로 분할하거나 LGM으로 결합했다.
이어서 클래스 레벨의 Afferent Coupling, Efferent Coupling 그리고 응집도를 측정했다.
결과는 4개의 연구 질문에 답하기 위해 AHP를 적용한 뒤 비교되었으며, 측정 결과에 기반해 다음과 같은 결론이 도출되었다:
- DDD의 사용은 MSA의 최적화된 세분화도를 찾는 데 있어 좋은 수단임이 증명되었다.
- 결합도와 응집도를 계산하는 것은 최적화된 Bounded Context를 찾는데 도움이 되었다.
현재(2021년) MSA의 세분화도와 분할에 대한 연구의 73%는 기존 MSA를 분할하는 것에 초점을 맞추고 있다.
우리는 앞으로의 연구는 MSA를 처음부터 만드는 것에 초점을 맞춘 연구가 늘어날 것으로 예상하며,
설계 과정에서의 측정 결과는 이에 따라 중요해질 것이라 생각한다.
비록 문헌에서는 MSA의 적절한 크기와 세분화도를 찾는 것에 문제가 있다고 하지만,
우리는 이것이 모듈화와 관련된 문제라고 믿는다.
물론 수많은 요소가 개입하는 상황에서 MSA의 적절한 크기를 찾는 것은 쉬운 일이 아니다.
DDD가 모듈화 된 MSA를 찾는 좋은 결과를 도출했다는 우리의 관측은 더 많은 예시가 뒷받침되어야 한다.
(이하 생략)
Introduction
실제 논문에선 연구에 대한 소개와 기존 문헌 리뷰, 그리고 DDD와 MSA의 최적화된 세분화도에 대해 설명한다.
해당 부분을 요약하는 것도 나름의 의미가 있겠지만, 나는 연구의 핵심 질문과 그 측정값을 요약하는데 집중할까 한다.
이 연구의 목적은 두 가지이다:
- DDD가 MSA의 최적화된 세분화도를 이끌어내는가?
- 응집성과 결합에 대한 계산이 최적화된 Bounded Context를 식별하는데 도움이 되는가?
위와 같은 목적을 가진 연구에서, 다음의 네 가지 RQ(Research Question)에 대한 측정값을 얻는 것을 목표로 한다:
- 마이크로서비스의 크기가 작다는 것이 느슨한 결합도를 의미하는가?
- 마이크로서비스의 크기가 커지면 응집도가 증가하는가?
- 결합도의 최솟값과 응집도의 최댓값이 MSA의 최적화된 세분화도를 정의하는가?
- DDD가 마이크로서비스의 최적화된 세분화도를 이끌어내는가?
Case Studies
위 질문에 대답하기 위해 직접 예시를 만들기보다 문헌 분석을 통해 두 가지의 적절한 모델을 선택했다.
첫 번째 예시는 UML(Unified Modeling Language) 다이어그램을 기반으로 하며,
두 번째 예시는 eShopOnContainers(쇼핑몰 앱)이고, 두 예시 모두 DDD를 적용하여 제안된 솔루션이다.
결합도는 Afferent Coupling과 Efferent Coupling을 기반으로 측정되었다.
어셈블리 수준에서 측정되는 Afferent Coupling 값은 아래와 같이 계산할 수 있다.
(Ca)i 를 i 어셈블리에 대한 Afferent Coupling이라고 하자. 여기서 n은 어셈블리의 개수이다.
Avg(Ca)=∑ni=1(Ca)in
Efferent Coupling은 현재 어셈블리 내부에서 사용되는 타입이 외부 어셈블리에서 참조되는 횟수를
측정하여 계산된다. 높을수록 외부 어셈블리에 대한 의존도가 높다는 뜻이다.
(Ce)i 를 i 어셈블리에 대한 Efferent Coupling이라고 하자. 여기서 n은 어셈블리의 개수이다.
Avg(Ce)=∑ni=1(Ce)in
이어서 응집력에 대한 계산이다. 응집력을 H 라고 할 때, 다음과 같이 계산되는데,
R을 어셈블리 내부의 타입 사이의 관계 수라고 하고, 타입의 개수를 N이라고 하면 아래와 같다.
H=R+1N
이어서 관계 응집도의 평균을 구해보자.
Hi를 어셈블리 i의 관계 응집도라고 하고, n을 어셈블리의 개수라고 하면 아래와 같다.
Avg(H)=∑ni=1Hin
Case Study 1
첫 예시는 DDD를 기반으로 한 화물 관련 도메인 모델이다. 본 스터디에서는 해당 UML 클래스 다이어그램을 기본으로 삼았다.
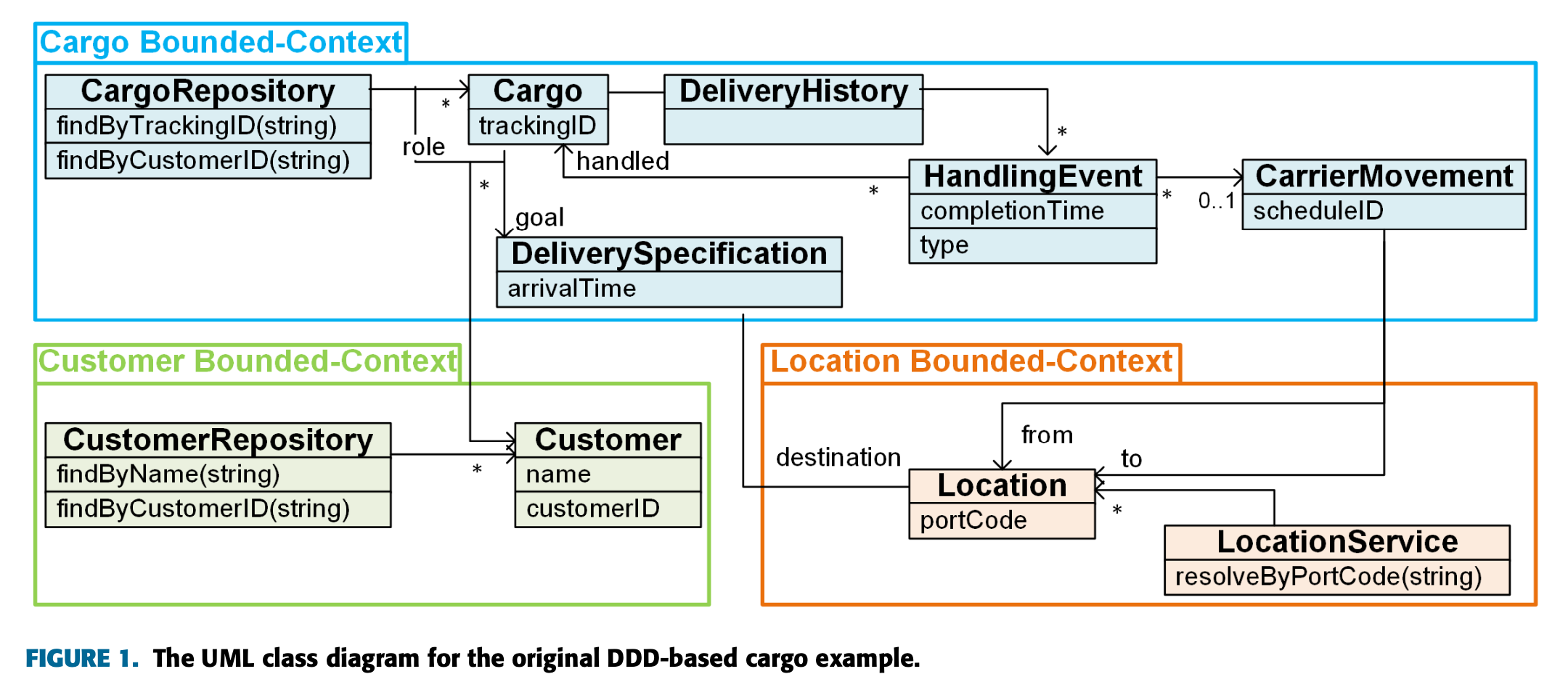
해당 도메인 모델의 UML 다이어그램이다.
그림에서 보듯이 세 개의 Bounded Context(화물, 고객, 위치를 가지고 있으며 각각의 목적과 역할을 가지고 있다.
위의 예제를 아래와 같은 더 작은 구성요소로 나눌 수 있다.
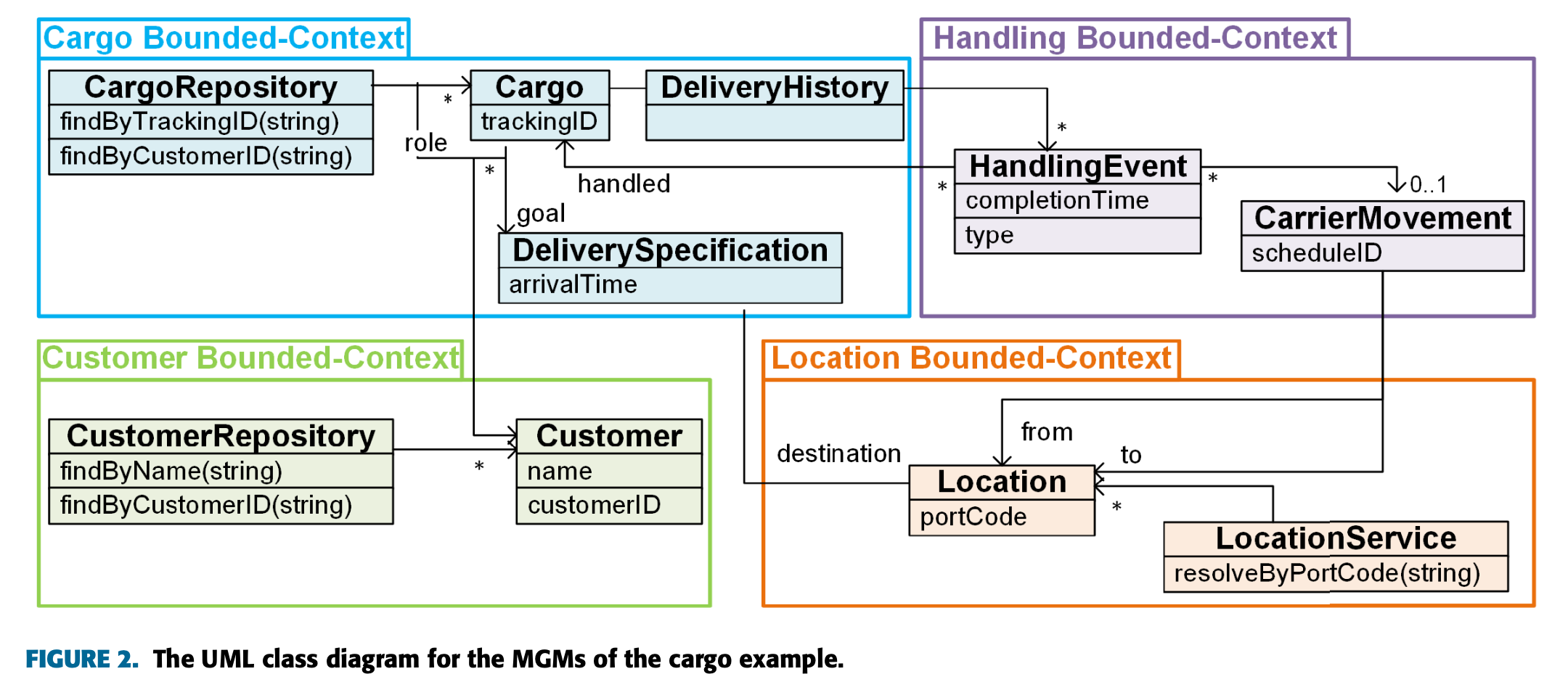
그 결과로 우리가 MGM이라고 부르는 예제가 구성되었다.
이전 연구들은 SOA와 MSA의 주요 차이점이 크기와 결합도임을 제시하고 있다.
여기서는 해당 설계 수정이 결합도와 응집도에 미치는 영향을 분석하는 것이 목적이다.
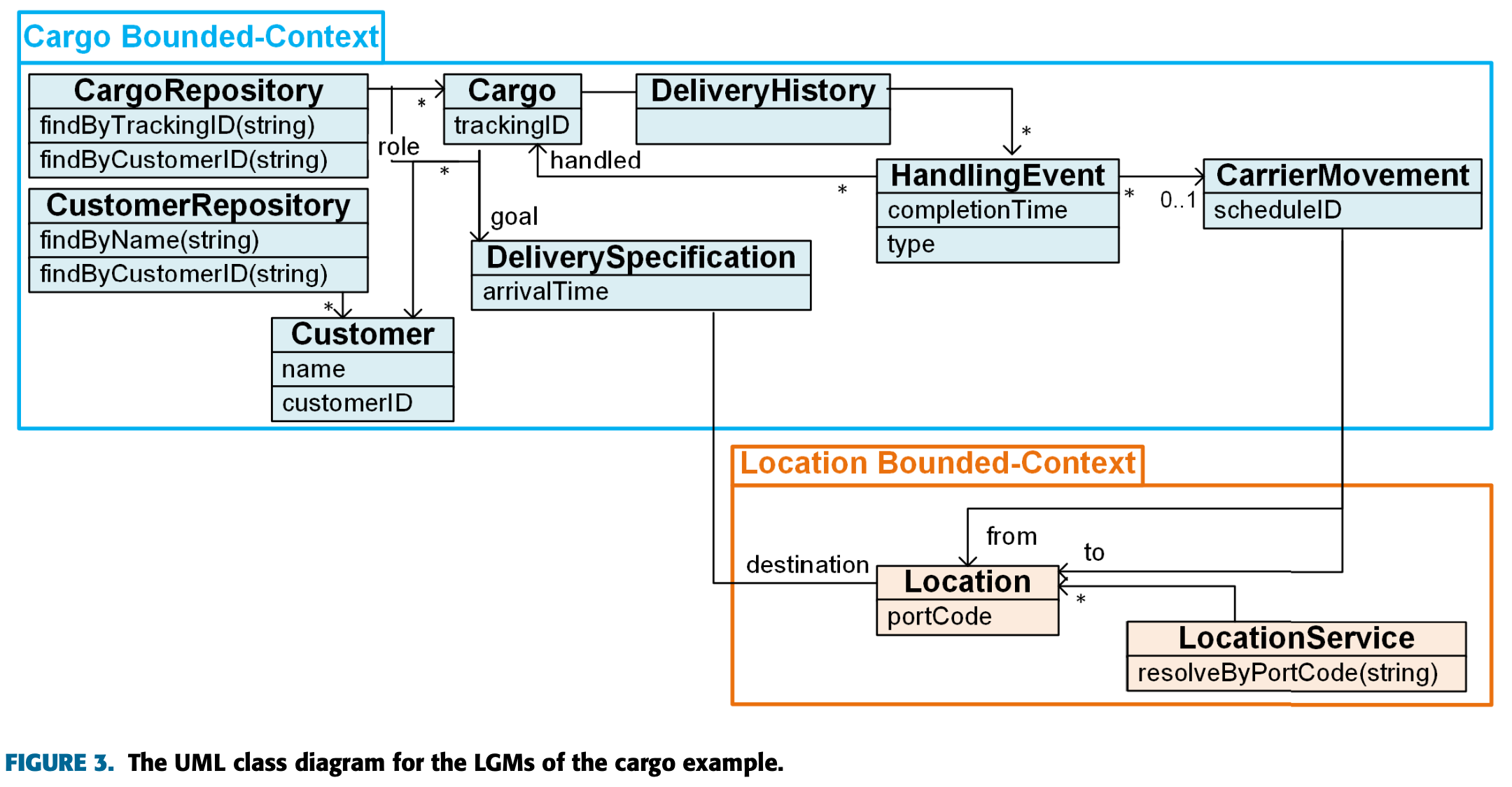
이를 위해 원래 예제의 세분화 수준을 낮춰 위와 같은 LGM을 구성했다.
이 설계의 목적은 기존 모델과 MGM, LGM 간의 응집도와 결합도 비교를 위한 것이다.
계속해서 위에 유도한 수식을 이용해서 값을 얻어내면 아래와 같은 결론을 얻을 수 있다.
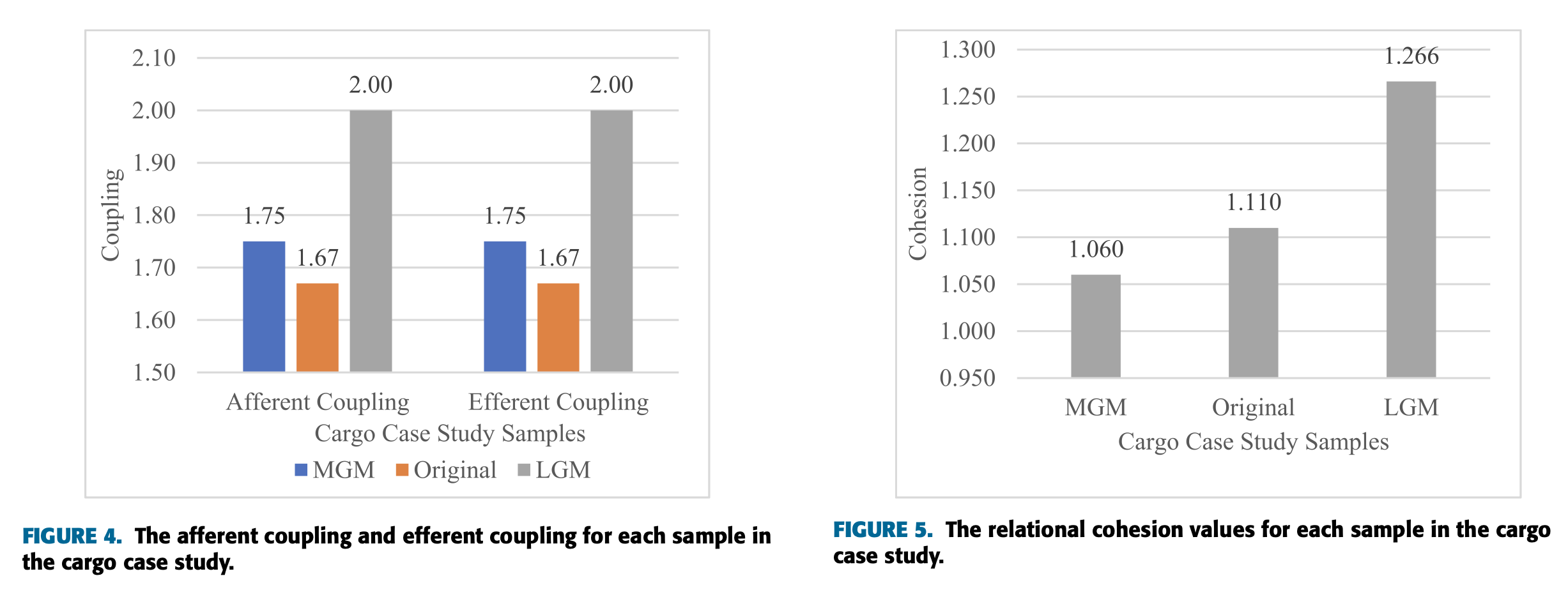
간단히 해석하자면 Afferent Coupling과 Efferent Coupling은 원본 예제에서 가장 작고, LGM에서 가장 크다.
또한 그림 5에서 볼 수 있듯이 Bounded Context의 크기가 커질수록 응집도가 증가한다. LGM이 가장 좋은 값을 가진다.
Case Study 2
다음으로는 많이 알려진 이커머스 웹 앱에 대한 측정이다.
해당 예제는 도커에서 실행되는 마이크로서비스 앱 eShopOnContainers이며, 7개의 마이크로서비스 중 연구에서 관심 있는
네 가지 서비스는 아래와 같다.
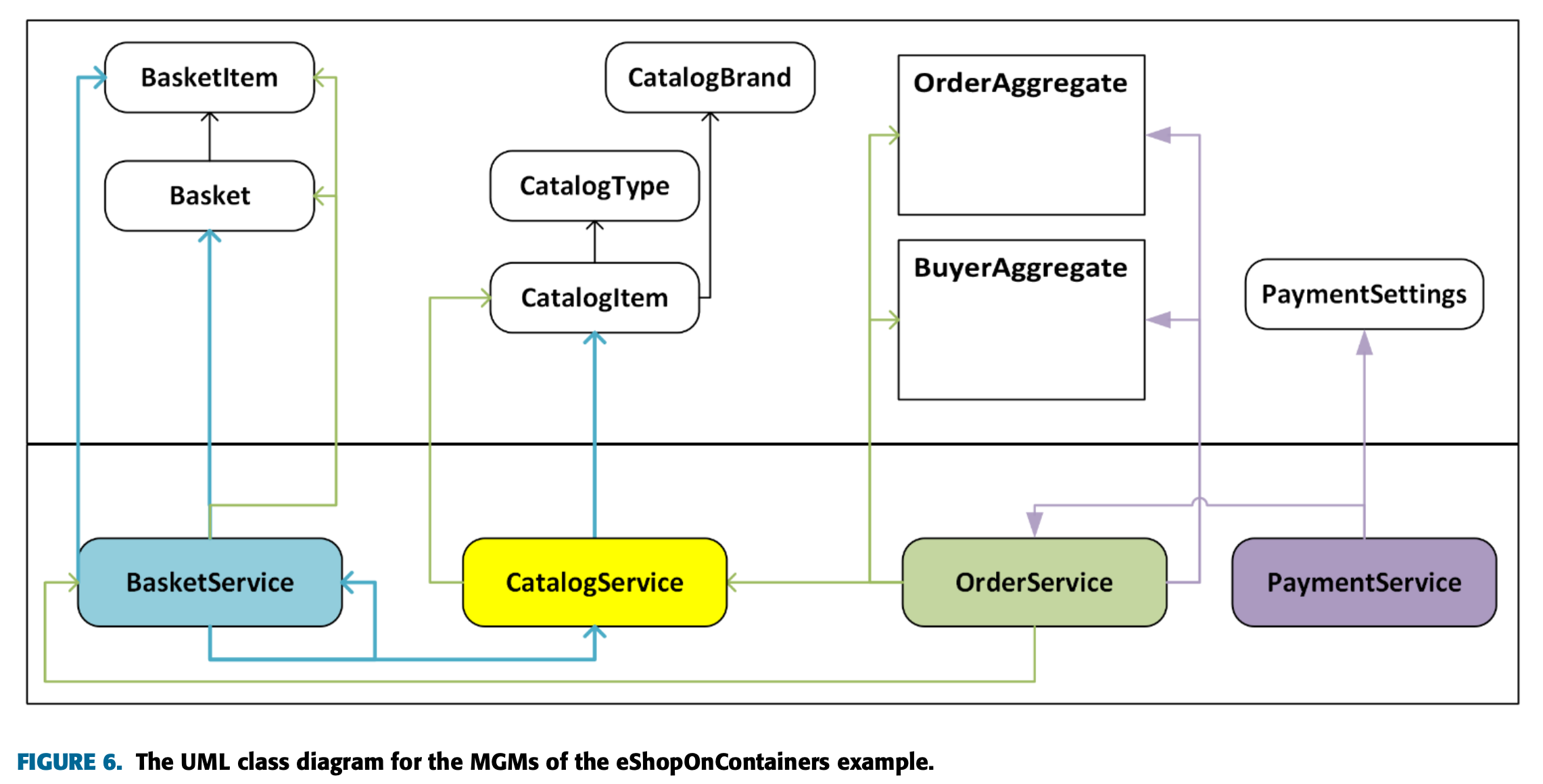
이 연구에서는 위 예제를 수정하여 아래와 같은 LGM과 MGM을 얻는다.
이어서 각 예제의 결합도와 응집도를 측정한다.
아래는 평균 Afferent Coupling과 Efferent Coupling, 그리고 응집도에 대한 계산 결과이다.
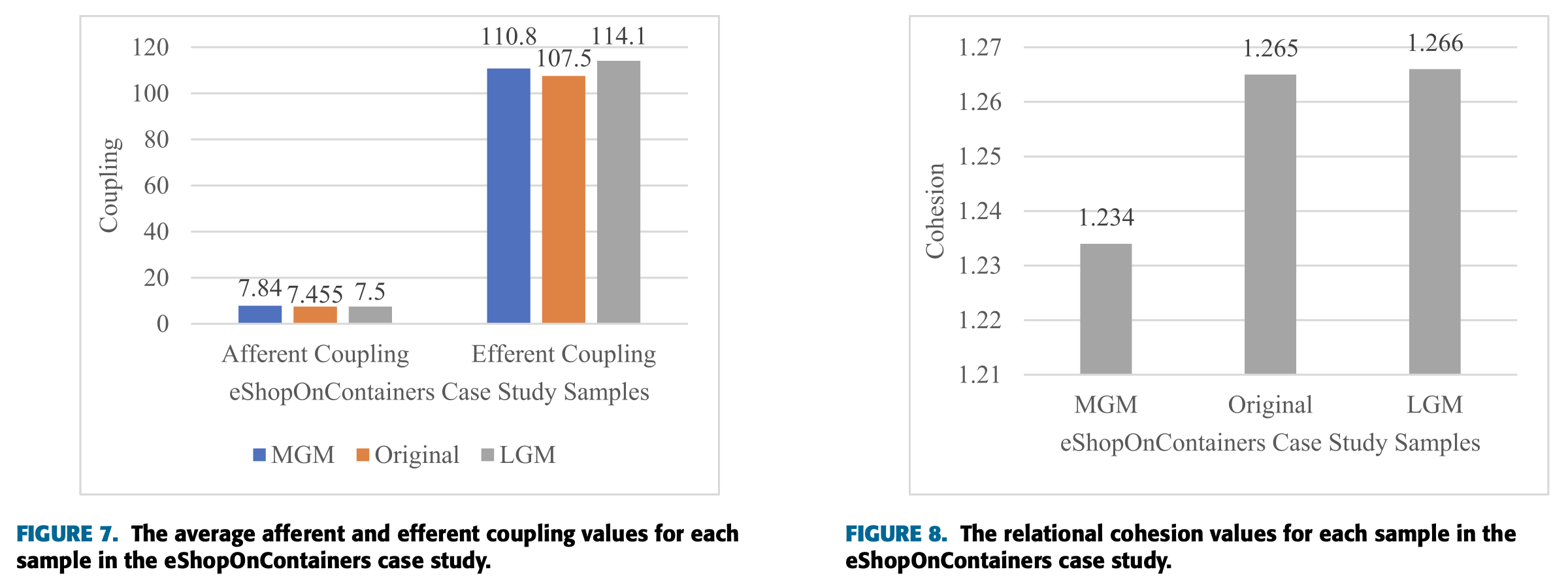
평균 Afferent Coupling과 Efferent Coupling 값은 원래의 예제에서 가장 작은 것으로 나타났다.
다만 Afferent Coupling은 MGM에서, Efferent Coupling은 LGM에서 가장 크게 나타났다.
응집성은 MGM, Original, LGM 순으로 증가하며, MGM과 원래 예제의 차이가 원래 예제와 LGM의 차이보다 두드러진다.
Analysis of Mesurements
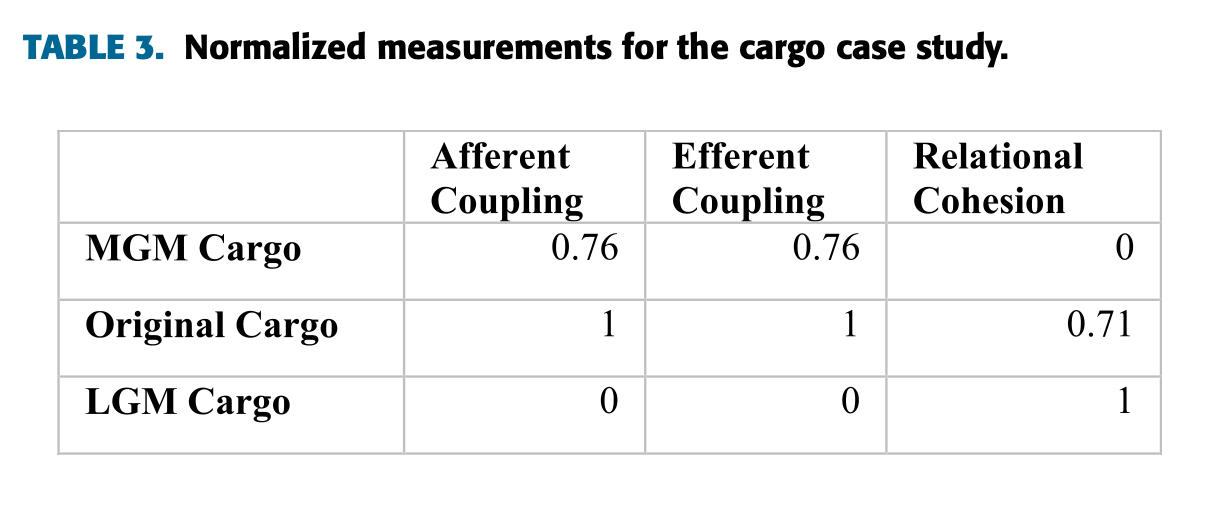
위의 표는 측정된 값을 아래의 공식(min-max scalar normalization)에 의해 정규화된 값이다.
s′k=sk−minmax−min
위 공식을 따라 정규화를 마치면, 가장 좋은 값은 1, 나쁜 값은 0으로, 그 사이의 값은 최솟값과의 비율로 나타난다.
최종 문제는 다중목적 결정 문제(MCDM - Multiobjective Decision-Making)
이를 위해 정규화된 값을 이용해 AHP를 적용하면, 각각 아래와 같은 결과를 얻을 수 있다.
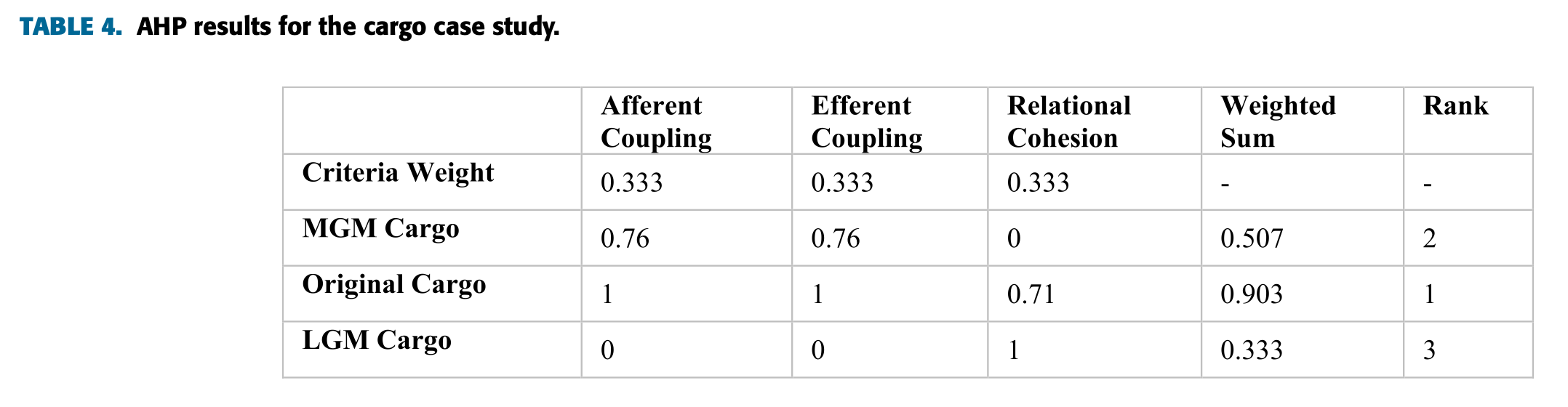
위 표는 화물 케이스 스터디의 결과를 보여준다. 가장 좋은 해결책은 원래의 예이며, 다음으로 MGM, 이어서 LGM이다.
이 부분에서 논문에는 LGM이 두 번째라고 적혀있는데 아무래도 오타인 것 같다.

위 표는 두 번째 케이스에 대한 정규화 값이다. 계속해서 AHP 결과를 보면 아래와 같다.
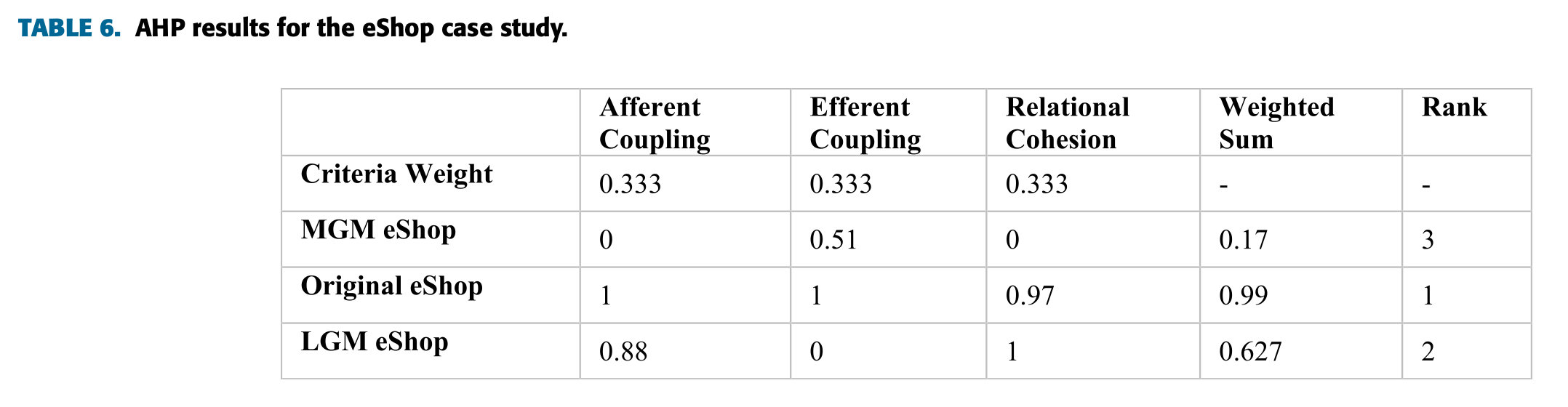
역시 가장 좋은 케이스는 원래의 케이스인 것으로 나타났다.
Discussion
마지막으로 결과를 바탕으로 논문 초반에 제시한 네 가지 질문에 대해 하나씩 답을 해보자.
- 마이크로서비스의 크기가 작다는 것이 느슨한 결합도를 의미하는가?
MGM과 LGM 모두 원본 케이스보다 높은 결합도를 가졌다.
모놀리식에서 마이크로서비스로의 이동은 결합 감소로 이어질 것으로 예상된다.
하지만 그림 4와 7에서 볼 수 있듯이 더 작은 마이크로서비스가 항상 결합도를 낮추는 것은 아니다. - 마이크로서비스의 크기가 커지면 응집도가 증가하는가?
위와 같은 특정 예에서는 마이크로서비스의 크기 증가가 응집력 증가로 나타났다.
하지만 이는 일반적인 규칙으로 보기에는 충분한 예시가 아니며, 더 많은 조사가 필요하다. - 결합도의 최솟값과 응집도의 최댓값이 MSA의 최적화된 세분화도를 정의하는가?
그림 4와 7에서 보듯 결합도는 원래 예제에서 가장 좋다. 그림 8에 의하면 응집도는 LGM에서 가장 좋다.
그러나 응집도의 증가는 결합도의 감소에 비해 두드러지지 않는다.
따라서 중간 결과를 선택하는 것처럼 쉬운 선택이 존재하지는 않는다.
이를 해결하기 위해 AHP를 적용한 결과 원래 앱이 최적화된 결과를 가지는 것으로 나타났으며,
결합도와 응집도는 DDD에서 최적화된 Bounded Context를 식별하는데 도움이 된다. - DDD가 마이크로서비스의 최적화된 세분화도를 이끌어내는가?
주어진 케이스 스터디에서 최적화된 세분화도는 원래 케이스에서 달성되었다.
두 스터디 모두 원래 DDD 컨셉을 따라 작성되었으며,
특정 예제에서는 DDD가 최적화된 세분화도를 이끌어내는 것으로 볼 수 있다.
'Development > Paper Review' 카테고리의 다른 글
| [Kafka]Kafka: a Distributed Messaging System for Log Processing (0) | 2023.09.17 |
|---|---|
| [MSA]Monolithic vs. MSA: 성능과 확장성 평가(10.1109/ACCESS.2022.3152803) (8) | 2023.04.10 |
| [MSA]뜬금 논문 리뷰 - j.jss.2022.111521 (0) | 2023.03.31 |
- Total
- Today
- Yesterday
- 스프링
- 야경
- 면접 준비
- 세계여행
- Algorithm
- 파이썬
- 지지
- 맛집
- 알고리즘
- 스트림
- 유럽여행
- RX100M5
- 백준
- 세계일주
- 리스트
- 세모
- 남미
- spring
- 칼이사
- 여행
- 유럽
- 자바
- Backjoon
- a6000
- Python
- 기술면접
- 중남미
- 동적계획법
- BOJ
- java
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

