티스토리 뷰
목차
오랜만에, 그리고 다소 뜬금없이 파이토치에 대한 글이다.
지난 글에 이어 아주 기초적인 코드를 가지고 데이터 준비부터 모델 학습 및 평가까지의 과정을 알아보려 한다.
총 세 개의 완전 연결층(Fully Connected Layer)로 이루어진 기초적인 MLP 모델이며
활성화 함수는 ReLU를, 과적합 방지를 위해 드롭 아웃을, 손실함수는 MSE, 최적화 알고리즘은 Adam을 사용하였다.
나도 이 단어의 나열이 정확히 무엇을 뜻하는지는 모른다. 코드를 보며 정리해보자.
선 요약
먼저 오늘 구현할 코드와 결과는 다음과 같다:
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
import torch
from torch import nn, optim
from torch.utils.data import DataLoader, Dataset
import torch.nn.functional as F
import matplotlib.pyplot as plt
df = pd.read_csv('./data/reg.csv', index_col=[0])
df.head(10)
X = df.drop('Price', axis=1).to_numpy()
Y = df['Price'].to_numpy().reshape((-1, 1))
class TensorData(Dataset):
def __init__(self, x_data, y_data):
self.x_data = torch.FloatTensor(x_data)
self.y_data = torch.FloatTensor(y_data)
self.len = self.y_data.shape[0]
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
def __len__(self):
return self.len
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5)
trainsets = TensorData(X_train, Y_train)
trainloader = DataLoader(trainsets, batch_size=32, shuffle=True)
testsets = TensorData(X_test, Y_test)
testloader = DataLoader(testsets, batch_size=32, shuffle=False)
class Regressor(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(13, 50, bias=True)
self.fc2 = nn.Linear(50, 30, bias=True)
self.fc3 = nn.Linear(30, 1, bias=True)
self.dropout = nn.Dropout(0.2)
def forward(self, x):
x = F.relu(self.fc1(x))
x = self.dropout(F.relu(self.fc2(x)))
x = F.relu(self.fc3(x))
return x
model = Regressor()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-2, weight_decay=1e-7)
ep = 0
ls = 1
loss_ = []
n = len(trainloader)
for epoch in range(200):
running_loss = 0.0
for data in trainloader:
inputs, values = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, values)
loss.backward()
optimizer.step()
running_loss += loss.item()
l = running_loss / n
loss_.append(l)
if l < ls:
ls = l
ep = epoch
torch.save({'epoch': ep,
'loss': loss_,
'model': model.state_dict(),
'optimizer': optimizer.state_dict()
}, './models/reg4-1.pt')
print('Finished Training')
plt.figure(figsize=(10, 8))
plt.plot(loss_)
plt.title("Training Loss")
plt.xlabel("epoch")
plt.show()
checkpoint = torch.load ('./models/reg4-1.pt', weights_only=True)
model.load_state_dict(checkpoint['model'])
optimizer.load_state_dict(checkpoint['optimizer'])
loss_ = checkpoint['loss']
ep = checkpoint['epoch']
ls = loss_[-1]
print(f"epoch={ep}, loss={ls}")
def rmse(dataloader):
with torch.no_grad():
square_sum = 0
num_instances = 0
model.eval()
for data in dataloader:
inputs, targets = data
outputs = model(inputs)
square_sum += torch.sum((outputs - targets) ** 2).item()
num_instances += len(targets)
model.train()
return np.sqrt(square_sum / num_instances)
train_rmse = rmse(trainloader)
test_rmse = rmse(testloader)
print("Train RMSE: %.5f" % train_rmse)
print("Test RMSE: %.5f" % test_rmse)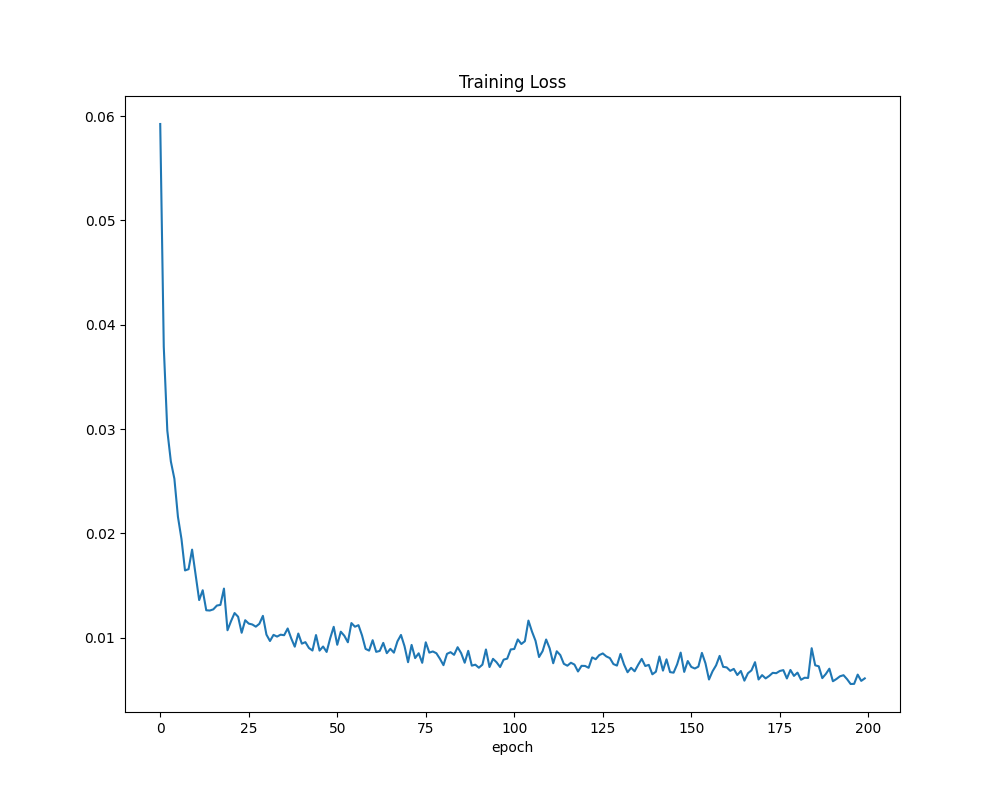
Finished Training
epoch=195, loss=0.005551515176193789
Train RMSE: 0.06559
Test RMSE: 0.11336
또한, 핵심 워크플로우는 아래와 같은데,
- 데이터 준비
- pandas, numpy를 활용해 데이터를 전처리하고, PyTorch의 Dataset과 DataLoader로 모델에 입력 가능한 형식으로 변환한다.
- MLP 모델 정의
- 다층 퍼셉트론(Multi-Layer Perceptron) 구조를 설계하고, 활성화 함수(ReLU)와 정규화 기법(드롭아웃)을 활용한다.
- 손실 함수와 최적화
- 손실 함수로 평균 제곱 오차(MSE), 최적화 알고리즘으로 Adam을 사용하여 모델의 학습 속도와 안정성을 높인다.
- 모델 학습
- 에포크(epoch)와 배치(batch)를 기반으로 순전파와 역전파를 반복하며 모델의 가중치를 점진적으로 업데이트한다.
- 모델 평가
- RMSE 지표를 통해 학습 데이터와 테스트 데이터에 대한 모델의 성능을 평가하고, 일반화 능력을 확인한다.
계속해서 코드를 가능한 한 샅샅이 뜯어보자.
라이브러리 불러오기
import pandas as pd # 데이터를 다루기 위한 라이브러리
import numpy as np # 수학 연산에 강력한 라이브러리
from sklearn.model_selection import train_test_split # 데이터를 학습용과 테스트용으로 나누기 위한 도구
# PyTorch 관련 모듈 (딥러닝 프레임워크)
import torch
from torch import nn, optim # nn: 신경망 구성 도구, optim: 최적화 알고리즘
from torch.utils.data import DataLoader, Dataset # 데이터를 신경망에 쉽게 전달하도록 도와주는 도구
import torch.nn.functional as F # 활성화 함수(ReLU 등)와 같은 기능 제공
# 그래프를 그리기 위한 도구
import matplotlib.pyplot as plt
이 부분은 모델을 만들기 위한 라이브러리와 도구를 불러오는 과정이다.
pandas
import pandas as pd # 데이터를 다루기 위한 라이브러리pandas는 데이터 분석과 조작을 위한 라이브러리이다.
주로 데이터프레임(DataFrame) 형태로 데이터를 다루며,
여기서 데이터프레임은 행(Row)과 열(Column)로 구성된 표 같은 구조를 가리킨다.
이 예제에서는 CSV 파일을 읽어오고 데이터를 가공하거나 확인하는 데 사용된다.
예: 데이터 불러오기(read_csv), 데이터 확인(head), 데이터 전처리(drop 등).
numpy
import numpy as np # 수학 연산에 강력한 라이브러리numpy는 배열 연산을 위한 라이브러리로, 대규모 다차원 배열(Array)과 행렬(Matrix)을 쉽게 처리할 수 있도록 해준다.
이 예제에서 데이터를 넘파이 배열 형태로 변환하여 PyTorch 모델에 전달한다.
딥러닝 모델은 데이터를 다룰 때 주로 숫자로 이루어진 배열을 사용하므로, numpy는 데이터 처리를 쉽게 해준다고 할 수 있다.
예: 데이터 전처리, 배열 변환, 수학적 계산 등.
scikit-learn, train_test_split
from sklearn.model_selection import train_test_split # 데이터를 학습용과 테스트용으로 나누기 위한 도구scikit-learn은 머신러닝 모델을 쉽게 구현하고 평가할 수 있는 라이브러리이다.
당연히 파이썬 기반 라이브러리로, 데이터 전처리, 모델 학습, 평가, 그리고 하이퍼파라미터 튜닝 등의 기능을 제공한다.
주요 기능:
- 데이터 전처리 (Scaling, Encoding 등)
- 지도 학습 모델 (회귀, 분류)
- 비지도 학습 모델 (클러스터링, 차원 축소)
- 모델 선택 및 평가 (교차 검증, 성능 측정)
- 도구: 데이터 분할, 파이프라인 생성 등.
train_test_split은 데이터를 학습용 데이터(Training Set)와 테스트용 데이터(Test Set)로 분리하는 함수이다.
머신러닝 및 딥러닝에서 데이터를 나누는 것은 매우 중요한 과정인데, 그 이유는 다음과 같다:
- 학습 데이터는 모델의 가중치를 학습시키는 데 사용.
- 테스트 데이터는 학습된 모델이 새로운 데이터에 대해 얼마나 잘 작동하는지 평가.
- 학습 데이터와 테스트 데이터를 분리하지 않으면, 모델이 학습한 데이터로 평가하게 되어, 성능이 과대평가될 수 있음.
간단한 사용법은 다음과 같다:
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5)
- 입력 파라미터:
- X: 입력 데이터 (독립 변수, 예측을 위한 특성값).
- Y: 출력 데이터 (종속 변수, 예측 대상값).
- test_size: 테스트 데이터 비율 (0.0~1.0 사이의 값). 예제에서는 50%를 테스트 데이터로 설정.
- random_state: 랜덤 분할 시드. 고정하면 항상 동일하게 나뉜다.
- shuffle: 데이터를 섞을지 여부. 기본값은 True.
- 출력 결과:
- X_train: 학습용 입력 데이터.
- X_test: 테스트용 입력 데이터.
- Y_train: 학습용 출력 데이터.
- Y_test: 테스트용 출력 데이터.
PyTorch
파이토치에 대해서는 이전 글에 적었으므로 생략한다.
[PyTorch]갑자기 써보는, PyTorch에 대하여
[PyTorch]갑자기 써보는, PyTorch에 대하여
목차 PyTorch는 딥러닝에 사용되는 오픈소스 라이브러리이다. 이름처럼 파이썬과 궁합이 좋으며, Numpy 등을 텐서로 가져올 수 있고 GPU 가속 기능(CUDA)을 지원한다. 이 글에선 파이토치를 학습하기
gnidinger.tistory.com
import torchPyTorch의 핵심 라이브러리로, 텐서(Tensor)를 생성하고 연산할 수 있다.
텐서는 numpy 배열과 비슷하지만, GPU를 사용한 연산이 가능하며, 이로 인해 딥러닝 모델 학습 속도가 크게 향상된다.
from torch import nn, optim # nn: 신경망 구성 도구, optim: 최적화 알고리즘- nn (신경망 관련 도구):
- 딥러닝 모델의 구성 요소를 제공한다.
- 예: nn.Linear (선형 회귀 연산), nn.MSELoss (평균 제곱 오차 손실 함수) 등.
- optim (최적화 도구):
- 모델의 가중치를 업데이트하는 최적화 알고리즘을 제공한다.
- 예: optim.Adam, optim.SGD 등.
from torch.utils.data import DataLoader, Dataset- Dataset: 데이터셋을 정의하는 클래스.
- 학습/테스트 데이터를 PyTorch 모델이 처리할 수 있는 형태로 변환한다.
- DataLoader: 데이터셋에서 데이터를 작은 배치(batch) 단위로 불러온다.
- 배치를 사용하면 메모리 효율이 좋아지고 학습을 안정적으로 할 수 있다.
- shuffle=True 옵션으로 데이터를 무작위로 섞어 학습할수도 있다.
import torch.nn.functional as F- PyTorch에서 제공하는 다양한 함수가 포함된 모듈.
- 활성화 함수(Activation Function): 뉴런의 출력을 비선형적으로 만들어주는 함수.
- 예: F.relu (ReLU 활성화 함수).
- 기타 유틸리티: 다양한 수학적/통계적 연산을 지원한다.
matplotlib
import matplotlib.pyplot as plt
matplotlib는 데이터를 시각화하는 데 사용된다.
딥러닝 학습 과정에서 손실 값(loss)이나 정확도(accuracy) 변화를 시각적으로 확인할 수 있다.
이 예제에서는 학습 손실 그래프를 그리기 위해 사용한다.
정리하면:
- pandas와 numpy로 데이터를 읽고, 전처리하고, 모델에 적합한 형태로 변환.
- train_test_split으로 데이터를 학습용과 테스트용으로 분리.
- PyTorch를 사용해 딥러닝 모델을 정의하고, 학습 및 평가 진행.
- matplotlib로 학습 과정에서 손실 변화 추이를 시각화.
가 되겠다. 계속 가자.
데이터 불러오기
df = pd.read_csv('./data/reg.csv', index_col=[0]) # 데이터 파일(.csv) 불러오기
df.head(10) # 데이터의 처음 10개 행을 출력 (데이터 확인)pd.read_csv는 pandas 라이브러리에서 제공하는 함수로,
CSV(Comma-Separated Values) 파일을 읽어와 데이터프레임(DataFrame)으로 변환한다.
위에도 적었지만 데이터프레임(DataFrame)이란 행(row)과 열(column)로 이루어진 2차원 데이터 구조로,
테이블처럼 데이터를 다룰 수 있는 형태이다.
- './data/reg.csv':
읽어올 CSV 파일의 경로.
./는 현재 작업 디렉토리를 나타낸다. 이 위치에 data라는 폴더가 있고, 그 안에 reg.csv 파일이 있다는 의미이다.
파일 이름이 맞지 않거나 경로가 잘못되면 파일을 찾을 수 없다는 에러(FileNotFoundError)가 발생한다. - index_col=[0]
CSV 파일의 첫 번째 열(인덱스 0)을 데이터프레임의 행 인덱스(index)로 사용하겠다는 의미.
행 인덱스는 데이터프레임에서 각 행을 고유하게 식별하는 역할을 한다.
예를 들어, 행 번호 대신 특정 열의 값을 기준으로 행을 참조할 수도 있다.
CSV 파일의 구조가 아래와 같다고 가정해 보자:
ID,Feature1,Feature2,Price
1,100,200,300000
2,150,250,400000
3,120,220,350000여기서 첫 번째 열인 ID를 행 인덱스로 설정하면, 데이터프레임은 다음과 같이 보인다:
Feature1 Feature2 Price
ID
1 100 200 300000
2 150 250 400000
3 120 220 350000이와 같이 데이터의 고유 ID나 식별자 역할을 하는 열을 인덱스로 사용하면 데이터 관리가 용이하다.
추가로 head()는 데이터프레임의 상위 몇 개의 행을 출력하는 함수이다. 이 코드에서는 10줄.
데이터를 넘파이 배열로 변환하기
X = df.drop('Price', axis=1).to_numpy() # 타겟값(Price)을 제외한 입력 데이터
Y = df['Price'].to_numpy().reshape((-1,1)) # 타겟값(Price)을 넘파이 배열로 변환위에서 빼먹었는데, 여기서 사용할 데이터는 아래와 같이 생겼다:
,x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,Price
0,0.034632928990378856,0.20691874294461926,0.13705683524618398,0.5405257875427069,0.19394063802447586,0.6992387409019816,0.6305316835806476,0.23941002898632566,0.027374902595528224,0.20985690453868694,0.347608848147062,0.9963940895380002,0.10264397961253241,0.4222222222222222
1,0.0289202299459708,0.01431455569545709,0.2761127083137239,0.255945340880795,0.6188861329172837,0.5554070016518993,0.7822633031459153,0.48297656338310796,0.10303068383436612,0.10669035862272963,0.5207755728752816,0.9966503269493703,0.18711954207000414,0.36888888888888893
2,0.020627377516973758,0.03322997947619249,0.2811157434130778,0.5255907655009844,0.16526854437106514,0.6241015338868727,0.5860047674159798,0.27271335047551454,0.03600976804922804,0.1069856709403868,0.5953007139610871,0.9832838882175655,0.08407879935246144,0.66
3,0.022748634819668066,0.03380107378604885,0.1250442315136054,0.26325276748899507,0.2515093671242243,0.6585321451306905,0.43216033241996654,0.34493168496407706,0.15001803194000074,0.06831744294967851,0.6512973205386736,0.9899891552141605,0.01598961970103027,0.6311111111111111
4,0.022148110073693862,0.029373549635402015,0.12105722098401409,0.5211260496171771,0.39966962669663897,0.44808565700625985,0.5201578438918822,0.4953416360731683,0.10438342287333918,0.06935957260718734,0.5601160247799375,0.9987225758811824,0.09278201945294202,0.6933333333333334
5,0.03865146804691113,0.019568487115940794,0.13944913754113641,0.7198519634775946,0.560580997773553,0.6105313245974302,0.5786614818560172,0.3879263713268743,0.13362941508795623,0.0729674488602573,0.5140782158555341,0.9863852555582414,0.12739568020059328,0.5266666666666666총 14개의 열로 구성되며 각 열에 대한 설명은 다음과 같다:
- x1 ~ x13: 집값을 예측하는 데 사용되는 특징값들(특성).
- 각 열은 하나의 특징(feature)을 나타내며, 숫자로 표현된다. 예: x1, x2 등.
- 예를 들어, x1은 어떤 지역적 요소를 나타낼 수 있고, x2는 해당 지역의 인프라 수준을 나타낼 수 있다.
- Price: 타겟값(집값). 모델이 예측하려고 하는 목표값이다.
계속해서 이 코드 블록의 목표는 입력 데이터와 출력 데이터를 구분하는데 있으며,
- 입력 데이터 X: x1에서 x13까지의 값을 포함.
- 출력 데이터 Y: Price 열을 포함.
과 같이 나눌 수 있다. 계속해서 코드를 보자.
X = df.drop('Price', axis=1).to_numpy()Price 열을 제외하고 나머지 열(x1 ~ x13)만 선택한다.
선택한 데이터프레임은 다음과 같이 생기게 된다.
x1 x2 x3 ... x13
0 0.0346 0.2069 0.1370 ... 0.1026
1 0.0289 0.0143 0.2761 ... 0.1871
2 0.0206 0.0332 0.2811 ... 0.0840
3 0.0227 0.0338 0.1250 ... 0.0159
4 0.0221 0.0294 0.1211 ... 0.0928이어서 .to_numpy()는 데이터프레임을 넘파이 배열로 변환하며, 아래와 같은 모습이 된다.
[[0.0346 0.2069 0.1370 ... 0.9964 0.1026]
[0.0289 0.0143 0.2761 ... 0.9967 0.1871]
[0.0206 0.0332 0.2811 ... 0.9833 0.0840]
[0.0227 0.0338 0.1250 ... 0.9899 0.0159]
[0.0221 0.0294 0.1211 ... 0.9987 0.0928]]각 행은 하나의 샘플이고, 열은 하나의 특징을 나타낸다.
Y = df['Price'].to_numpy().reshape((-1, 1))여기서는 Price열만 선택하게 된다. 데이터 프레임은 다음과 같고,
0 0.4222
1 0.3689
2 0.6600
3 0.6311
4 0.6933
Name: Price, dtype: float64넘파이 배열로 변환하면 다음과 같다.
[0.4222 0.3689 0.6600 0.6311 0.6933].reshape((-1, 1))은 배열을 2차원 형태로 변환하는데, 그 이유는 파이토치가 2차원 형태의 입력을 요구하기 때문이다.
최종 모습은 다음과 같다.
[[0.4222]
[0.3689]
[0.6600]
[0.6311]
[0.6933]]왜 2차원이 필요한가?
딥러닝 모델, 특히 PyTorch의 신경망은 데이터를 배치 단위로 처리한다. 즉, 데이터를 다음과 같은 형태로 받으며,
입력 데이터 형태: (N,F)
- N (Batch Size): 샘플의 개수. 한 번에 처리할 데이터의 묶음.
- F (Feature Size): 하나의 샘플에서 사용할 특성의 개수.
따라서 입력과 출력 모두 2차원 이상의 배열로 제공해야 한다.
또한 파이토치는 입력과 출력이 같은 차원이어야 한다고 가정한다고 한다.
reshape((-1, 1))가 필요한 이유:
- Y는 예측하려는 타겟값(집값)으로, 각 샘플에 하나의 출력값이 대응된다.
- 1차원 배열인 경우, Y는 단순히 값들의 나열로 간주되기 때문에, 샘플 개수와 특성의 개수를 명시적으로 나타내지 못한다.
- 2차원 배열로 바꿔야만 PyTorch가 이를 "배치의 크기 × 출력값의 크기"로 이해할 수 있다.
.reshape((-1, 1))의 동작 원리
reshape 메서드는 배열의 모양(Shape)을 변경한다.
(-1, 1)의 의미:
- -1: 배열의 첫 번째 차원을 자동 계산하라는 의미입. 배열의 총 원소 수를 기준으로 첫 번째 차원을 계산한다.
- 1: 두 번째 차원은 1로 고정.
우리의 예제를 사용하면:
배열 Y = [0.4222, 0.3689, 0.6600]이 있을 때:
- 원래 형태: (3,) (1차원, 길이 3)
- reshape((-1, 1)) 적용:
- 첫 번째 차원을 자동으로 계산: 3개의 값 → (3, 1) 형태로 변환
- 결과:
[[0.4222],
[0.3689],
[0.6600]]
데이터셋 클래스 정의
class TensorData(Dataset):
def __init__(self, x_data, y_data):
self.x_data = torch.FloatTensor(x_data) # 입력 데이터를 텐서로 변환
self.y_data = torch.FloatTensor(y_data) # 출력 데이터를 텐서로 변환
self.len = self.y_data.shape[0] # 데이터 길이(샘플 개수)
def __getitem__(self, index):
return self.x_data[index], self.y_data[index] # 주어진 인덱스의 데이터 반환
def __len__(self):
return self.len # 데이터셋 길이 반환
여기서 TensorData 클래스는 PyTorch의 Dataset을 상속받아 만든 사용자 정의 데이터셋이다.
이 클래스는 데이터를 PyTorch에서 신경망 모델에 전달할 수 있는 형식으로 변환하고,
데이터 배치 처리와 같은 기능을 가능하게 한다.
조금 더 알아보면, PyTorch의 Dataset 클래스는 데이터를 다루기 위한 기본 구조를 제공한다.
Dataset을 상속받으면, 데이터셋에 포함된 데이터를 정의하고 어떻게 반환할지를 커스터마이징할 수 있다.
PyTorch의 DataLoader와 함께 사용하여 데이터를 배치 단위로 나누고, 섞거나 반복적으로 제공할 수 있다.
즉, TensorData 클래스는 사용자가 제공한 x_data(입력 데이터)와 y_data(타겟값)를
PyTorch 모델이 처리할 수 있도록 변환하고, 각 샘플에 인덱스로 접근할 수 있는 기능을 제공한다고 할 수 있다.
코드를 더 뜯어보면 다음과 같다.
def __init__(self, x_data, y_data):
self.x_data = torch.FloatTensor(x_data) # 입력 데이터를 텐서로 변환
self.y_data = torch.FloatTensor(y_data) # 출력 데이터를 텐서로 변환
self.len = self.y_data.shape[0] # 데이터 길이(샘플 개수)__init__ 메서드는 일종의 생성자 역할을 한다.
- 입력 인자
- x_data: 입력 데이터(특성값, 예: 방의 크기, 위치 등).
- y_data: 출력 데이터(목표값, 예: 집값).
- 주요 역할
- torch.FloatTensor로 변환:
- PyTorch는 데이터를 텐서(Tensor) 형태로 처리한다.
따라서 numpy 배열(x_data, y_data)을 FloatTensor로 변환한다. - 변환된 텐서는 GPU 연산(CUDA)도 가능해진다.
- PyTorch는 데이터를 텐서(Tensor) 형태로 처리한다.
- 데이터 길이(len) 계산:
- self.len = self.y_data.shape[0]는 데이터셋의 샘플 개수를 저장한다.
- 이 값은 나중에 데이터셋 길이를 반환하는 데 사용된다.
- torch.FloatTensor로 변환:
def __getitem__(self, index):
return self.x_data[index], self.y_data[index] # 주어진 인덱스의 데이터 반환이 메서드는 특정 인덱스의 샘플을 반환한다.
PyTorch의 DataLoader가 TensorData 객체에서 데이터를 로드할 때 호출되며, 작동 방식은 아래와 같다:
- self.x_data[index]: 입력 데이터에서 주어진 인덱스(index)에 해당하는 샘플을 반환.
- self.y_data[index]: 타겟 데이터에서 주어진 인덱스에 해당하는 값을 반환.
- (x, y) 형태로 반환한다. 이때 x는 입력 데이터(특성값), y는 타겟값(예측하려는 값)이다.
예를 들자면 아래와 같다.
dataset = TensorData(X_train, Y_train) # TensorData 객체 생성
x, y = dataset[0] # 0번째 샘플 가져오기여기서 x는 0번째 입력 데이터, y는 0번째 타겟값이다.
def __len__(self):
return self.len # 데이터셋 길이 반환이 메서드는 데이터셋의 샘플 개수를 반환한다.
파이토치는 데이터 로딩시 반복 횟수를 결정하기 위해 __len__을 사용한다.
왜 이런 구조가 필요한가?
PyTorch는 데이터셋을 효율적으로 관리하고 모델에 전달하기 위해 Dataset과 DataLoader를 사용한다.
- Dataset 클래스:
데이터를 로드하고 특정 인덱스의 샘플을 반환하는 로직을 정의. - DataLoader 클래스:
Dataset에서 정의된 데이터를 배치 단위로 나누고, 무작위로 섞거나 순차적으로 반복하도록 도와줌.
마지막으로 전체 흐름을 요약하면 다음과 같고,
TensorData 객체 생성:
dataset = TensorData(X_train, Y_train)
DataLoader로 배치 생성:
trainloader = DataLoader(dataset, batch_size=32, shuffle=True)
DataLoader에서 배치를 모델에 전달:
for inputs, targets in trainloader:
outputs = model(inputs) # 모델에 데이터 전달
나같은 초심자를 위해 핵심을 요약하면 다음과 같다:
- TensorData 클래스의 역할:
- 데이터를 텐서로 변환하고, Dataset의 기본 구조를 재정의하여 PyTorch 모델과 호환되도록 만든다.
- __getitem__으로 특정 데이터를 가져오고, __len__으로 데이터셋 크기를 알려준다.
- Dataset과 DataLoader는 모델 학습 과정에서 데이터를 효율적으로 관리하는 핵심 요소이다.
데이터를 학습용과 테스트용으로 나누기
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5)
trainsets = TensorData(X_train, Y_train)
trainloader = DataLoader(trainsets, batch_size=32, shuffle=True)
testsets = TensorData(X_test, Y_test)
testloader = DataLoader(testsets, batch_size=32, shuffle=False)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5)- train_test_split 함수는 데이터를 무작위로 섞어 학습용과 테스트용으로 나눈다.
- 여기서 test_size=0.5는 전체 데이터의 50%를 테스트 데이터로 사용하겠다는 의미이다.
- 학습용 데이터(X_train, Y_train)는 모델을 학습시키는 데 사용한다.
- 테스트용 데이터(X_test, Y_test)는 학습한 모델이 얼마나 잘 동작하는지 평가하는 데 사용한다.
- 데이터를 섞어서 나누기 때문에 특정 데이터가 학습용 또는 테스트용으로 고정되지 않고, 일반화된 평가를 가능하게 한다.
trainsets = TensorData(X_train, Y_train)
testsets = TensorData(X_test, Y_test)- TensorData 클래스를 사용해 데이터를 PyTorch가 처리할 수 있는 텐서 형태로 변환한다.
- trainsets는 학습용 데이터를 텐서로 변환한 데이터셋이다.
- testsets는 테스트용 데이터를 텐서로 변환한 데이터셋이다.
- 이 과정은 PyTorch 모델이 데이터를 학습하거나 평가할 때 데이터를 올바른 형식으로 사용할 수 있도록 한다.
trainloader = DataLoader(trainsets, batch_size=32, shuffle=True)
testloader = DataLoader(testsets, batch_size=32, shuffle=False)- DataLoader는 데이터를 효율적으로 처리하기 위해 사용한다.
- batch_size=32는 데이터를 한 번에 32개씩 묶어서 처리한다. 이를 배치(batch)라고 부른다.
- 배치 처리는 메모리 사용량을 줄이고, 연산을 병렬화하여 학습 속도를 높인다.
- shuffle=True는 학습 데이터를 매번 무작위로 섞는다.
- 데이터를 섞으면 모델이 데이터의 순서에 의존하지 않고 더 일반화된 학습을 할 수 있다.
- 테스트 데이터는 섞을 필요가 없으므로 shuffle=False로 설정한다.
- trainloader는 학습 데이터를, testloader는 테스트 데이터를 모델에 전달하기 위해 사용한다.
역시 핵심을 요약하면 다음과 같다:
- 데이터 나누기: train_test_split로 데이터를 학습용(50%)과 테스트용(50%)으로 나눈다.
- 데이터 텐서화: TensorData를 이용해 데이터를 PyTorch가 이해할 수 있는 텐서 형태로 변환한다.
- DataLoader 생성: DataLoader를 사용해 데이터를 배치 단위로 나누고, 학습 시에는 데이터를 무작위로 섞는다.
MLP 모델 정의
다층 퍼셉트론(Multi-Layer Perceptron, MLP)은 여러 층의 뉴런(노드)으로 구성된 인공신경망이다.
입력층, 은닉층, 출력층으로 나뉘며 각 층은 입력값을 받아 계산을 수행하고 다음 층으로 전달한다.
조금 더 자세한 설명은 코드를 읽은 다음에 하도록 하자.
class Regressor(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(13, 50) # 입력층(13개 특징값) -> 첫 번째 은닉층(50개 노드)
self.fc2 = nn.Linear(50, 30) # 첫 번째 은닉층 -> 두 번째 은닉층(30개 노드)
self.fc3 = nn.Linear(30, 1) # 두 번째 은닉층 -> 출력층(1개 값: 집값)
self.dropout = nn.Dropout(0.2) # 과적합 방지를 위한 드롭아웃(20%)
def forward(self, x): # 모델의 연산 순서 정의
x = F.relu(self.fc1(x)) # 첫 번째 레이어 + 활성화 함수(ReLU)
x = self.dropout(F.relu(self.fc2(x))) # 두 번째 레이어 + 드롭아웃 + ReLU
x = F.relu(self.fc3(x)) # 마지막 레이어 + ReLU
return x- fc1: 첫 번째 완전 연결층이다. 입력값(13개 특징)을 받아 50개의 노드로 연결한다.
- nn.Linear(13, 50)는 입력 13개, 출력 50개인 선형 변환을 수행한다.
- 각 연결에는 가중치(weight)와 바이어스(bias)가 포함된다.
- fc2: 두 번째 완전 연결층이다. 첫 번째 층의 출력(50개)을 받아 30개의 노드로 연결한다.
- fc3: 출력층이다. 두 번째 층의 출력(30개)을 받아 하나의 값(집값)을 출력한다.
- Dropout(0.2): 과적합을 방지하기 위한 정규화 기법이다. 학습 시 매번 20%의 노드를 무작위로 제외한다.
- forward(x): 모델이 입력 데이터를 처리하는 연산 흐름을 정의한다.
- F.relu(self.fc1(x)): 첫 번째 층에서 선형 변환을 수행한 후 ReLU 활성화 함수를 적용한다.
- self.dropout(F.relu(self.fc2(x))): 두 번째 층에서 선형 변환, ReLU 적용 후 드롭아웃을 수행한다.
- F.relu(self.fc3(x)): 마지막 층에서 선형 변환과 ReLU 활성화 함수를 적용한다.
다층 퍼셉트론(Multi-Layer Perceptron, MLP)
- 구조
MLP는 하나 이상의 은닉층(hidden layer)을 가진 신경망이다. 각 층의 뉴런(노드)은 이전 층의 모든 노드와 연결된다(완전 연결층). - 가중치와 바이어스
각 연결은 학습 가능한 가중치(weight)와 바이어스(bias)를 가진다.
입력값에 가중치를 곱하고 바이어스를 더해 선형 변환을 수행한다.
이 과정에서 데이터의 패턴과 특징을 학습한다. - 활성화 함수
ReLU(Rectified Linear Unit)와 같은 활성화 함수는 신경망에 비선형성을 추가한다.
비선형성은 복잡한 데이터 패턴을 학습하는 데 필수적이다.
예를 들어, ReLU는 음수 입력을 0으로, 양수 입력은 그대로 반환한다. - 출력층
출력층의 활성화 함수는 문제 유형에 따라 다르게 선택된다.
- 회귀 문제에서는 활성화 함수를 사용하지 않아 연속값을 출력한다.
- 분류 문제에서는 소프트맥스(softmax)나 시그모이드(sigmoid) 함수를 사용한다.
우리 코드에서는 회귀문제임에도 마지막 층에서 활성화함수를 사용하는데, 이는 집값이 음수로 나오는 것을 막기 위함이다.
- 장점
- 단순한 데이터부터 복잡한 데이터까지 다양한 문제를 해결할 수 있다.
- 은닉층의 개수와 뉴런의 수를 조정해 유연한 설계가 가능하다.
- 한계
- 은닉층이 너무 많아지면 계산 비용이 증가하고 학습이 어려워질 수 있다(기울기 소실 문제).
- 이미지나 시계열 데이터와 같이 특정 구조적 특징을 가진 데이터에는 CNN이나 RNN이 더 적합하다.
레이어 사이의 연산
여기서 레이어 사이의 연산을 한 번 상세히 정리하고 지나가자.
실습 위주로 배우는 나에겐 꼭 필요한 시간이라 정리한다.
선형 변환 (Fully Connected Layer)
각 층에서 입력값 X와 가중치 행렬 W, 바이어스 벡터 b를 이용해 다음과 같은 선형 변환이 이루어진다:

- 연산 과정
1. 입력 데이터 X와 가중치 행렬 W를 행렬 곱(Matrix Multiplication)한다.
2. b를 Z의 각 행에 더한다(브로드캐스팅).
활성화 함수
활성화 함수는 각 노드의 출력값 Z에 비선형성을 추가한다.
ReLU(Rectified Linear Unit)의 연산은 다음과 같다:
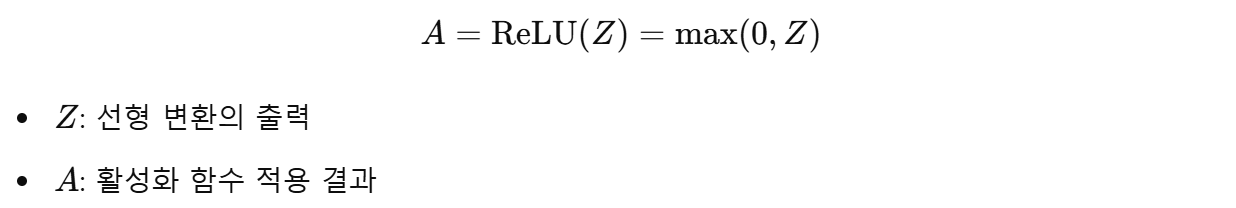
- ReLU의 역할
1. 양수 값은 그대로 출력한다.
2. 음수 값은 0으로 변환해 비선형성을 부여한다.
드롭아웃
드롭아웃은 학습 과정에서 무작위로 일부 뉴런을 비활성화한다.
드롭아웃 비율이 0.2라면, 20%의 노드가 무작위로 제외된다.
제외된 노드의 출력은 0으로 설정된다.
각 층의 연산 예시
- 첫 번째 레이어 연산
x = F.relu(self.fc1(x)) # fc1: nn.Linear(13, 50)
- 두 번째 레이어 연산
x = self.dropout(F.relu(self.fc2(x))) # fc2: nn.Linear(50, 30)
- 세 번째 레이어 연산(출력층)
x = F.relu(self.fc3(x)) # fc3: nn.Linear(30, 1)
- 요약

가중치 행렬 (W)와 바이어스 벡터 (b)
- 가중치 행렬 (W)
입력 데이터와 출력 데이터 간의 관계를 학습하는 핵심 요소다. 다른 말로 하면 입력값이 출력값에 미치는 영향을 조정한다.
입력값에 곱해져 각 뉴런의 중요도를 조정한다.
학습을 통해 입력 특징의 중요도를 학습한다. - 바이어스 벡터 (b)
가중치 행렬만으로 설명되지 않는 데이터를 보정하는 역할을 한다.
뉴런의 출력값에 일정 값을 더해주는 역할을 한다.
데이터의 분포를 더 잘 맞추기 위한 일종의 보정 역할을 한다.
- 초기값
- 가중치 (W): 일반적으로 작은 난수로 초기화한다.
- 바이어스 (b): 일반적으로 0으로 초기화한다.
- 초기화 방식
초기값은 신경망의 학습 효율에 영향을 준다.
- Xavier 초기화: W를 입력 노드와 출력 노드의 수를 기준으로 초기화.
- He 초기화: ReLU 활성화 함수와 함께 사용되며, 입력 노드의 수를 기준으로 초기화.
PyTorch에서는 자동으로 적절한 초기값을 설정하지만, nn.init 모듈을 사용해 직접 설정할 수도 있다.
- 업데이트 과정
가중치와 바이어스는 역전파(Backpropagation)과정에서 손실 함수의 기울기를 기반으로 업데이트된다.

- 요약
- 가중치 (W): 입력 특징의 중요도를 학습하며, 데이터와 모델 간의 관계를 형성한다.
- 바이어스 (b): 데이터의 분포를 보정하여 모델 성능을 개선한다.
- 초기화: W는 작은 난수, b는 0으로 초기화한다.
- 업데이트: 손실 함수의 기울기를 기반으로 가중치와 바이어스를 점진적으로 조정해 모델의 예측 능력을 향상시킨다.
손실 함수와 최적화 함수 정의
model = Regressor() # 모델 초기화
criterion = nn.MSELoss() # 손실 함수: 평균 제곱 오차 (MSE)
optimizer = optim.Adam(model.parameters(), lr=1e-2, weight_decay=1e-7)model = Regressor()- 이 코드는 Regressor 클래스를 사용하여 모델 객체를 생성하는 부분이다.
- Regressor는 위에서 정의한 딥러닝 모델로, 집값 예측을 위한 다층 퍼셉트론(Multi-Layer Perceptron, MLP) 구조를 가진다.
- model 변수는 학습 및 평가 과정에서 사용할 신경망 모델의 인스턴스를 나타낸다.
손실 함수: nn.MSELoss()
criterion = nn.MSELoss() # 손실 함수: 평균 제곱 오차 (MSE)- 손실 함수는 모델이 얼마나 잘 예측했는지, 또는 얼마나 틀렸는지를 측정하는 기준이다.
- 여기서 사용하는 nn.MSELoss는 평균 제곱 오차(MSE)를 계산한다.
- MSE는 예측값과 실제값의 차이를 제곱한 값의 평균으로 구한다.
- 제곱을 사용하기 때문에 차이가 클수록 손실 값이 크게 증가하여, 큰 오차를 더 강조한다.
- 계산식은 다음과 같다:
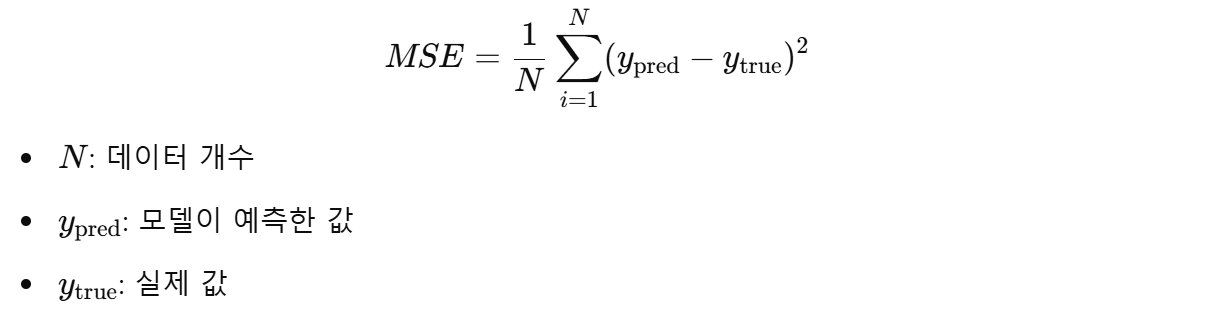
손실 값이 작을수록 모델의 예측이 실제 값과 가까워진다는 것을 의미한다.
왜 MSE를 사용하는가?
- 연속적인 값(집값)을 예측하는 회귀 문제에서는 MSE가 손실 함수로 자주 사용된다.
- 오차가 큰 예측값을 더 강하게 패널티로 적용하여, 모델이 더 정확한 예측을 하도록 유도한다.
회귀 문제?
회귀(Regression)는 연속적인 숫자 값을 예측하는 문제를 뜻한다.
"회귀"라는 단어는 데이터의 경향이 평균값을 중심으로 회귀(수렴)한다는 초기 발견에서 유래되었는데,
현대적으로는 통계학적으로 데이터를 분석하여 변수간의 관계를 수학적으로 모델링하고,
이를 바탕으로 미래의 값을 예측하는 과정을 의미한다.
즉, 주어진 입력 데이터를 바탕으로 실수형(continuous) 출력값을 생성하는 모델을 만드는 것이다.
회귀 문제는 입력 변수와 출력 변수 간의 연속적인 관계를 학습하는 것을 목표로 한다.
회귀문제의 특성은 다음과 같다:
- 출력값이 연속적인 값이다
- 회귀 문제의 가장 큰 특징은 출력값이 특정 범위 내에서 연속적인 값을 가질 수 있다는 것이다.
- 예: 키, 몸무게, 온도, 집값 등은 연속적인 값으로 나타난다.
- 입력 변수와 출력 변수 간의 관계
- 입력 변수(특징값)와 출력 변수(목표값) 간의 수학적 또는 통계적 관계를 학습한다.
- 입력과 출력이 선형적이거나 비선형적일 수 있다.
- 평가 지표
- 회귀 문제는 MSE(평균 제곱 오차), RMSE(평균 제곱근 오차), MAE(평균 절대 오차) 등 숫자 간의 차이를 계산하는 평가 지표를 사용한다.
- 분류 문제와 달리 정확도(Accuracy)와 같은 지표는 사용하지 않는다.
- 예측값의 범위
- 출력값은 특정 레이블(예: 0, 1)이 아니라 연속된 숫자로 표현된다.
- 예측값의 범위는 입력 데이터에 따라 달라질 수 있다.
최적화 함수: optim.Adam()
optimizer = optim.Adam(model.parameters(), lr=1e-2, weight_decay=1e-7)최적화 함수는 손실 값을 줄이기 위해 모델의 가중치(weight)와 바이어스(bias)를 업데이트하는 역할을 한다.
여기서 사용한 optim.Adam은 Adam(Adaptive Moment Estimation) 최적화 알고리즘이다.
- Adam 최적화 알고리즘의 특징
Adam은 SGD(확률적 경사 하강법)을 개선한 방법으로, 학습 속도와 안정성이 뛰어나다.
각 파라미터마다 적응형 학습률을 계산하여 업데이트를 수행한다.
모멘텀(momentum)과 RMSProp의 장점을 결합하여 경사면을 따라 더 빠르게 수렴하도록 돕는다. - Adam의 기본 업데이트 방식
모멘텀(momentum): 이전 기울기 정보의 지수를 계산하여 가속도를 더한다.
적응형 학습률: 가중치의 크기에 따라 학습률을 자동으로 조정한다. - Adam의 주요 하이퍼파라미터
학습률 (lr): 0.01로 설정되어 있다.
학습률은 한 번의 업데이트에서 가중치를 얼마나 크게 조정할지 결정한다.
너무 크면 발산할 수 있고, 너무 작으면 학습이 느리다. - L2 정규화 (weight_decay): 1e-7로 설정되어 있다.
L2 정규화는 과적합(overfitting)을 방지하기 위해 가중치 값이 너무 커지지 않도록 제약을 준다.
L2 패널티는 가중치의 제곱합을 추가적으로 손실에 더하는 방식으로 작동한다.
정규화에 대해서는 글을 따로 파서 알아보도록 하자.
- 요약: 손실 함수와 최적화 함수의 역할 관계
- 모델이 데이터를 학습하며 예측을 수행한다.
- 손실 함수가 예측값과 실제값의 차이를 계산하여 손실 값을 반환한다.
- 최적화 함수가 손실 값에 따라 가중치와 바이어스를 조정한다.
- 이 과정이 반복되면서 모델이 점점 더 정확한 예측을 하도록 학습한다.
모델 학습
ep = 0 # 가장 낮은 손실을 기록한 에포크를 저장할 변수
ls = 1 # 초기 손실 값, 비교 기준이 될 매우 높은 값으로 설정
loss_ = [] # 손실 값을 저장할 리스트
n = len(trainloader) # 배치 개수
for epoch in range(200): # 200번 학습
running_loss = 0.0
for data in trainloader: # 데이터 배치 단위로 가져오기
inputs, values = data # 입력값과 출력값 분리
optimizer.zero_grad() # 이전 기울기 초기화
outputs = model(inputs) # 모델에 데이터 입력 -> 예측값 산출
loss = criterion(outputs, values) # 예측값과 실제값 비교 -> 손실 계산
loss.backward() # 손실을 기준으로 역전파 수행
optimizer.step() # 가중치 업데이트
running_loss += loss.item() # 배치 손실 합산
l = running_loss / n # 에포크당 평균 손실 계산
loss_.append(l) # 손실 기록대망의 모델 학습 파트이다.
데이터를 반복적으로 모델에 입력하고, 손실을 계산하며, 모델의 가중치를 업데이트한다.
각 줄의 동작을 조금 더 자세히 살펴보자.
손실 값을 저장하기 위한 리스트와 배치 개수 정의
loss_ = [] # 손실 값을 저장할 리스트
n = len(trainloader) # 배치 개수- loss_ 리스트는 에포크(epoch)마다 평균 손실 값을 저장하기 위해 사용한다.
- trainloader는 학습 데이터셋을 작은 묶음(배치) 단위로 제공하는 객체이다.
- len(trainloader)는 전체 학습 데이터셋이 몇 개의 배치로 나뉘어 있는지 계산한다. 이는 에포크당 배치 손실 값을 평균 내는 데 사용된다.
에포크 루프
for epoch in range(200): # 200번 학습
running_loss = 0.0- for epoch in range(200)는 모델을 200번 반복 학습한다는 의미이다. 이 반복을 통해 모델은 입력 데이터와 출력 데이터 간의 관계를 점차 학습한다.
- running_loss는 한 에포크 동안 누적된 배치 손실 값을 저장하는 변수이다. 에포크가 끝날 때 평균 손실 값을 계산하기 위해 사용된다.
데이터 배치 단위 학습
for data in trainloader: # 데이터 배치 단위로 가져오기
inputs, values = data # 입력값과 출력값 분리- for data in trainloader는 학습 데이터를 trainloader에서 배치 단위로 가져온다. 배치 크기는 32로 설정되어 있으므로, 한 번에 32개의 데이터가 data 변수에 들어간다.
- data는 (inputs, values) 형태로 구성된다.
- inputs: 모델의 입력 데이터(X값)이다.
- values: 입력에 대응하는 실제 타겟값(Y값)이다.
기울기 초기화
optimizer.zero_grad() # 이전 기울기 초기화PyTorch에서는 이전 배치의 기울기 값이 다음 배치에도 영향을 미친다.
이를 방지하기 위해 optimizer.zero_grad()를 호출하여 기울기 값을 초기화한다.
모델 예측
outputs = model(inputs) # 모델에 데이터 입력 -> 예측값 산출
model(inputs)은 입력 데이터를 모델에 통과시켜 예측값을 산출한다.
모델의 forward 함수가 호출되어 순전파(forward propagation)가 이루어진다.
손실 계산
loss = criterion(outputs, values) # 예측값과 실제값 비교 -> 손실 계산criterion(outputs, values)는 예측값(outputs)과 실제값(values) 간의 차이를 계산하여 손실(loss)을 구한다.
이 손실 값은 모델이 얼마나 잘못 예측했는지를 나타낸다. 손실 값이 클수록 예측이 부정확하다는 의미이다.
역전파
loss.backward() # 손실을 기준으로 역전파 수행loss.backward()는 역전파(backpropagation)를 수행하여 각 가중치에 대한 기울기(gradient)를 계산한다.
역전파는 손실을 줄이기 위해 모델의 가중치를 어떻게 조정해야 하는지 방향을 제시한다.
가중치 업데이트
optimizer.step() # 가중치 업데이트optimizer.step()는 앞서 계산된 기울기를 기반으로 모델의 가중치를 업데이트한다.
이 단계에서 가중치는 손실을 줄이는 방향으로 조정된다.
배치 손실 누적
running_loss += loss.item() # 배치 손실 합산loss.item()은 현재 배치의 손실 값을 반환한다.
이 손실 값을 running_loss에 더하여 한 에포크 동안의 총 손실을 누적한다.
에포크 손실 계산 및 저장
l = running_loss / n # 에포크당 평균 손실 계산
loss_.append(l) # 손실 기록- l은 한 에포크 동안의 평균 손실 값이다. 총 손실 값(running_loss)을 배치 개수(n)로 나누어 계산한다.
- loss_ 리스트에 평균 손실 값을 추가하여, 학습 과정을 추적할 수 있도록 기록한다.
학습 과정 요약
- 데이터 준비: 배치 단위로 데이터를 가져온다.
- 순전파: 입력 데이터를 통해 예측값을 생성한다.
- 손실 계산: 예측값과 실제값 간의 차이를 계산한다.
- 역전파 및 업데이트: 손실을 줄이는 방향으로 모델의 가중치를 조정한다.
- 손실 추적: 한 에포크의 평균 손실 값을 기록한다.
이 과정을 여러 에포크 동안 반복하여 모델이 데이터를 점진적으로 학습한다.
학습 중 모델 저장
if l < ls: # 현재 에포크의 손실(l)이 이전까지의 최소 손실(ls)보다 작다면
ls = l # 최소 손실 값을 현재 손실로 업데이트
ep = epoch # 최소 손실이 기록된 에포크를 저장
torch.save({'epoch': ep, # 에포크 정보 저장
'loss': loss_, # 손실 기록 리스트 저장
'model': model.state_dict(), # 모델의 학습된 가중치 저장
'optimizer': optimizer.state_dict() # 옵티마이저 상태 저장
}, './models/reg4-1.pt') # 모델을 reg4-1.pt 파일로 저장위 코드는 학습 중 손실이 줄어들 때마다 모델의 현재 상태를 저장하여 나중에 사용할 수 있도록 한다.
대략 다음과 같은 과정으로 진행된다.
if l < ls: # 현재 에포크의 손실(l)이 이전 최소 손실(ls)보다 작다면- 조건문으로 최소 손실 비교:
- l은 현재 에포크의 평균 손실 값이다.
- 이 조건문은 현재 손실 값 l이 이전에 저장된 최소 손실 값 ls보다 작은지 확인한다.
- 목적: 손실이 감소했을 때만 모델을 저장하도록 한다. 불필요한 저장을 방지한다.
ls = l # 최소 손실 값을 현재 손실로 업데이트
ep = epoch # 최소 손실이 기록된 에포크 번호를 저장- 최소 손실 및 에포크 번호 업데이트:
- ls를 현재 손실 값 l로 업데이트하여 새로운 기준 손실 값으로 설정한다.
- ep를 현재 에포크 번호로 업데이트한다.
- 이렇게 하면 저장된 모델이 학습 중 가장 낮은 손실 값을 기록한 상태임을 보장한다.
torch.save({'epoch': ep, # 에포크 정보를 저장
'loss': loss_, # 손실 값 기록(리스트 형태)
'model': model.state_dict(), # 모델 가중치 및 바이어스 저장
'optimizer': optimizer.state_dict() # 옵티마이저 상태 저장
}, './models/reg4-1.pt') # reg4-1.pt 파일로 저장- 모델 저장:
- torch.save는 모델의 상태, 손실 기록, 옵티마이저 상태 등을 저장한다.
- 저장 내용은 딕셔너리 형태로 구성되어 있으며, 다음과 같은 정보를 포함한다:
- epoch: 저장 당시 에포크 번호. 나중에 학습을 이어갈 때 어디서부터 시작할지 확인할 수 있다.
- loss: 학습 동안의 손실 값 기록(리스트). 모델 성능 추이를 분석하거나 학습을 재개할 때 참고한다.
- model.state_dict(): 모델의 모든 학습된 파라미터(가중치와 바이어스)를 딕셔너리 형태로 저장한다.
- optimizer.state_dict(): 옵티마이저의 상태(학습률, 모멘텀, 현재의 가중치 업데이트 정보 등)를 저장한다.
- 저장 파일 경로:
- './models/reg4-1.pt': 모델이 저장될 파일 경로와 이름.
- .pt는 PyTorch 모델 파일의 확장자이다.
왜 이런 방식으로 저장하는가?
- 최적의 모델만 저장:
- 모든 에포크의 모델을 저장하면 불필요한 저장 공간 낭비와 관리의 어려움이 발생한다.
- 손실 값이 줄어들 때만 저장하여 최적의 상태를 기록한다.
- 학습 중단/재개 가능:
- 저장된 모델을 불러와 이전 학습 상태에서 이어갈 수 있다. 예를 들어, 서버가 중단되거나 장시간 학습을 할 때 유용하다.
- 평가/배포 시 유용:
- 학습이 완료된 모델을 다시 학습할 필요 없이, 저장된 상태를 불러와 곧바로 평가나 예측에 사용할 수 있다.
추가
- model.state_dict()와 torch.save()의 차이:
- model.state_dict()는 모델의 학습된 파라미터(가중치와 바이어스)만 저장한다.
- torch.save()는 다양한 정보를 저장할 수 있어 재학습 시 편리하다.
- 왜 옵티마이저 상태를 저장하는가?:
- 옵티마이저 상태를 저장하면, 재학습 시 학습률이나 모멘텀 같은 추가 정보를 유지할 수 있다. 이는 학습 곡선을 안정적으로 이어가는 데 필수적이다.
학습 결과 저장 및 시각화
plt.plot(loss_)
plt.title("Training Loss")
plt.xlabel("epoch")
plt.show()이 부분은 학습 과정에서의 손실 값(loss)의 변화를 시각적으로 확인하기 위해 그래프를 그리는 코드이다.
학습이 진행되면서 손실 값이 점차 감소하는지, 그리고 학습이 잘 이루어졌는지 확인하는 데 사용한다.
저장된 손실 값(loss_)을 "Training Loss"라는 제목과 "epoch", 즉 반복 횟수라는 x축을 사용해 선 그래프로 그린다.
저장된 모델 불러오기
이 부분은 이전에 학습 도중 저장했던 최적의 모델 상태를 다시 로드하는 과정이다.
Checkpoint 불러오기
checkpoint = torch.load('./models/reg4-1.pt') # 저장된 모델 상태를 불러온다- torch.load
- PyTorch에서 제공하는 함수로, 저장된 모델 파일(reg4-1.pt)을 메모리로 불러온다.
- 저장된 파일에는 딕셔너리 형태로 여러 정보가 담겨 있다.
- epoch: 저장 당시의 에포크 값.
- loss: 손실 기록 리스트.
- model: 모델의 가중치와 바이어스(state_dict).
- optimizer: 옵티마이저의 상태(state_dict).
- 왜 사용하는가?
- 학습 도중 저장했던 모델 상태를 그대로 복구해 추가 학습을 진행하거나, 저장된 모델을 평가 또는 예측에 사용할 수 있다.
모델 가중치 불러오기
model.load_state_dict(checkpoint['model']) # 저장된 모델의 가중치를 모델에 로드한다- model.load_state_dict
- 저장된 가중치와 바이어스를 현재 모델(model)에 적용한다.
- state_dict: PyTorch 모델의 가중치와 바이어스를 담고 있는 딕셔너리 형태의 데이터.
- 예: fc1.weight, fc1.bias 등 각 레이어의 가중치와 바이어스가 저장된다.
- 이 함수는 저장 당시와 동일한 모델 구조(Regressor)를 요구한다.
- 왜 필요한가?
- 저장된 모델의 학습된 가중치와 바이어스를 불러와야, 학습을 이어가거나 평가 시 이전 학습의 성능을 유지할 수 있다.
최적화 함수 상태 불러오기
optimizer.load_state_dict(checkpoint['optimizer']) # 저장된 옵티마이저 상태를 옵티마이저에 로드한다- optimizer.load_state_dict
- 저장된 옵티마이저 상태를 현재 옵티마이저에 복구한다.
- 옵티마이저 상태에는 다음 정보가 포함된다.
- 가중치 업데이트 정보: 학습률, 모멘텀 등의 옵티마이저 설정값.
- 현재 상태: 학습 중 계산된 변화량(예: Adam 옵티마이저의 1차, 2차 모멘텀 값).
- 왜 필요한가?
- 옵티마이저 상태를 불러오면, 저장된 시점의 학습 상태를 그대로 이어갈 수 있다.
- 만약 옵티마이저 상태를 복구하지 않으면, 학습 초기화로 간주되므로 이전 학습과 이어지지 않는다.
손실 기록과 에포크 값 복구
loss_ = checkpoint['loss'] # 저장된 손실 기록 리스트를 불러온다
ep = checkpoint['epoch'] # 저장된 에포크를 불러온다
ls = loss_[-1] # 저장된 손실 기록 중 마지막 값을 불러온다- loss_
- 학습 중 기록했던 손실 값 리스트를 복구한다.
- 손실 기록은 모델의 학습 상태를 시각화하거나, 학습 성능의 변화 과정을 검토하는 데 유용하다.
- ep
- 저장된 에포크 값을 복구한다.
- 이 값을 이용해 학습을 중단했던 시점부터 이어서 학습을 진행할 수 있다.
- ls
- 손실 리스트에서 마지막 값을 가져온다.
- 이는 저장 당시 모델의 마지막 손실 값을 의미한다.
- 이를 이용해 모델의 학습 성능을 간단히 확인할 수 있다.
모델 상태 출력
print(f"epoch={ep}, loss={ls}") # 저장된 모델의 에포크와 손실 값을 출력한다- 저장된 모델의 학습 상태를 확인하는 출력 부분이다.
- 출력 내용
- epoch: 모델이 저장될 당시의 학습 진행 상태.
- loss: 저장 당시의 손실 값.
출력 예시
epoch=185, loss=0.03456
모델 평가
def rmse(dataloader):
with torch.no_grad():
square_sum = 0
num_instances = 0
model.eval() # 평가 모드
for data in dataloader:
inputs, targets = data
outputs = model(inputs)
square_sum += torch.sum((outputs - targets) ** 2).item()
num_instances += len(targets)
model.train()
return np.sqrt(square_sum / num_instances)
train_rmse = rmse(trainloader) # 학습 데이터 RMSE
test_rmse = rmse(testloader) # 테스트 데이터 RMSE
print("Train RMSE: %.5f" % train_rmse)
print("Test RMSE: %.5f" % test_rmse)이 코드는 모델의 성능을 평가하는 데 사용한다.
RMSE(Root Mean Squared Error)를 계산해 학습 데이터와 테스트 데이터에 대한 예측 성능을 확인한다.
각 구문과 동작을 조금 더 살펴보자.
RMSE 계산 함수
def rmse(dataloader):
with torch.no_grad():
square_sum = 0
num_instances = 0
model.eval() # 평가 모드
for data in dataloader:
inputs, targets = data
outputs = model(inputs)
square_sum += torch.sum((outputs - targets) ** 2).item()
num_instances += len(targets)
model.train()
return np.sqrt(square_sum / num_instances)- with torch.no_grad():
- 평가 시에 사용한다. 역전파 계산을 비활성화해 메모리 사용량과 계산 시간을 줄인다.
- 학습이 아닌 단순 평가를 목적으로 하므로 필요 없는 기울기 계산을 방지한다.
- model.eval()
- 모델을 평가 모드로 전환한다.
- 학습 중에 사용된 드롭아웃(Dropout)과 배치 정규화(Batch Normalization)를 비활성화한다.
- 예측 시에는 이러한 기법이 적용되지 않아야 정확한 평가가 가능하다.
- 루프를 통한 데이터 처리
- for data in dataloader:는 데이터 로더에서 배치를 하나씩 가져온다.
- inputs는 입력 데이터이고, targets는 실제 정답 값이다.
- outputs = model(inputs)는 모델에 데이터를 넣어 예측값을 얻는다.
- 오차 제곱 합 계산
- (outputs - targets) ** 2는 예측값과 실제값의 차이를 제곱한다.
- torch.sum으로 모든 샘플의 오차 제곱을 합산한다.
- square_sum은 누적된 오차 제곱 합을 저장한다.
- 총 샘플 수 계산
- len(targets)는 현재 배치에 포함된 샘플의 개수를 반환한다.
- num_instances는 전체 데이터의 총 샘플 개수를 누적한다.
- model.train()
- 함수가 끝나기 전에 모델을 다시 학습 모드로 전환한다.
- 이후 학습을 진행할 때 모델의 동작이 정상적으로 돌아가도록 한다.
- np.sqrt
- 오차 제곱 합을 샘플 개수로 나누어 평균 제곱 오차(MSE)를 계산한다.
- 이 값을 제곱근으로 변환해 RMSE를 반환한다.
학습 데이터와 테스트 데이터 평가
train_rmse = rmse(trainloader) # 학습 데이터 RMSE
test_rmse = rmse(testloader) # 테스트 데이터 RMSE- train_rmse
- 학습 데이터(trainloader)를 기준으로 RMSE를 계산한다.
- 모델이 학습 데이터에 얼마나 잘 맞추는지 확인한다.
- test_rmse
- 테스트 데이터(testloader)를 기준으로 RMSE를 계산한다.
- 모델이 학습에 사용되지 않은 데이터에 대해 얼마나 잘 작동하는지 평가한다.
결과 출력
print("Train RMSE: %.5f" % train_rmse)
print("Test RMSE: %.5f" % test_rmse)%.5f는 소수점 다섯 자리까지 결과를 출력한다.
학습 데이터와 테스트 데이터 각각에 대한 RMSE를 비교해 모델의 일반화 성능을 평가한다.
일반화 성능: 테스트 데이터 RMSE가 낮다면, 모델이 새로운 데이터에 대해 잘 동작한다고 볼 수 있다.
정리
이렇게 해서 아주 기초적인 MLP 모델을 사용해 데이터 준비부터 모델 학습, 평가까지의 과정을 살펴보았다.
<데이터 전처리-모델 정의-손실 함수-최적화 함수-학습-평가>라는 딥러닝의 기본 워크플로우를 하나씩 뜯어보았는데,
처음이라 쉽지는 않았던 것 같다.
앞으로도 당분간은 쉬운 코드를 반복적으로 구현하고 뜯어보며 왜 이런 과정이 필요하고 어떤 영향을 끼치는지 이해해보려 한다.
'Python > PyTorch' 카테고리의 다른 글
| [Pytorch]Vanilla RNN과 확장된 기법들: LSTM, GRU, Bidirectional LSTM, Transformer (2) | 2024.12.03 |
|---|---|
| [PyTorch]전이 학습(Transfer Learning) (0) | 2024.11.27 |
| [PyTorch]Vanilla RNN을 활용한 코스피 예측 문제 (1) | 2024.11.26 |
| [PyTorch]CNN을 활용한 이미지 분류 문제(CIFAR-10) (1) | 2024.11.25 |
| [PyTorch]PyTorch 환경설정 및 MNIST 실습 (0) | 2023.08.30 |
| [PyTorch]갑자기 써보는, PyTorch에 대하여 (1) | 2023.08.26 |
- Total
- Today
- Yesterday
- BOJ
- java
- 남미
- 세계일주
- 리스트
- 여행
- 세계여행
- 중남미
- 야경
- 자바
- 칼이사
- 알고리즘
- a6000
- 맛집
- 면접 준비
- Algorithm
- 백준
- Backjoon
- 지지
- 유럽여행
- 스프링
- 동적계획법
- 유럽
- RX100M5
- Python
- 스트림
- 세모
- spring
- 기술면접
- 파이썬
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

