티스토리 뷰
문제
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다.
각 원판은 반경이 큰 순서대로 쌓여있다.
이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라.
단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.

입력
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
출력
첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다.
두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데,
이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.
풀이
드디어 재귀 단계의 마지막 문제다.
여기까지 왔지만 여전히 재귀에 대해선 잘 알 수가 없다.
우선 대충 재귀호출을 만들고 문제의 조건에 맞춰 수정을 거듭하며 풀어왔기 때문일 것이다.
계속 연습하면 좋은 일이 있을진 모르겠지만..
사실 이후의 단계에서도 이래저래 재귀호출은 계속되니 빨리 익숙해지면 좋겠다는 생각뿐.
아무튼 문제로 돌아가면, 재귀 로직 자체는 그렇게 어렵지 않은 것을 확인할 수 있다.
- 규칙을 찾고
- 가장 작은 단위로 쪼개고
- 쪼개진 가장 작은 단위부터 연산을 해 결과를 통합한다
순서대로 하나씩 진행해 보자.
규칙
먼저 n개의 원판을 목적지까지 옮기는 데 필요한 재귀 호출 횟수를 생각해 보자.
위 그림을 이용해 간소화해서 나타내면 아래와 같은 모양이 될 것이다.
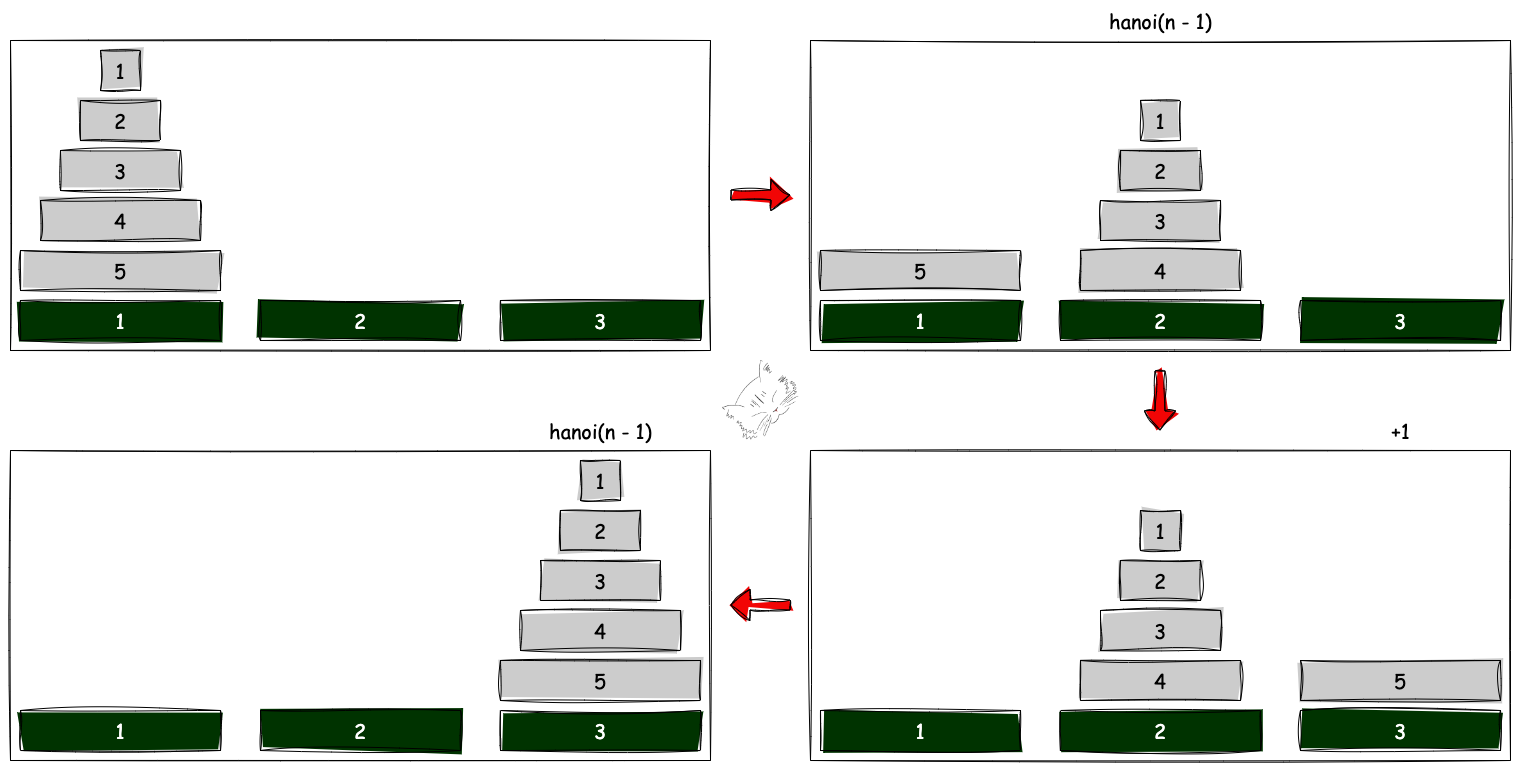
순서는 아래와 같다.
- 맨 아래의 원판이 목적지까지 가기 위해선 나머지 원판이 이외의 자리로 이동해야 한다(n - 1번 호출)
- 이후 맨 아래의 원판이 목적지로 이동한다(+1)
- 나머지 원판이 맨 아래의 원판 위로 이동한다(n - 1번 호출)
이상을 간단하게 함수로 나타내면 아래와 같이 된다.
이때 n은 정수이기 때문에 n번째 함숫값을 아래와 같은 일반항으로 표현하는 것이 언제나 가능하며,
이를 이용해 위 함수를 다시 적어 정리하면 다음과 같은 일반항을 얻을 수 있다.
위 일반항은 n개의 원판이 주어졌을 때 총 이동 횟수를 가리킨다.
쪼개기
위의 일반항을 이용해 원판의 이동 순서를 쪼개면 된다.
1에서 2로 이동해야 할 원판이 하나만 남을 때까지 재귀호출을 진행한 뒤에 목적지로 이동시키고 전 단계의 함수를 호출한다.
이때 호출되는 함수는 원판이 두 개일 경우의 함수가 되기 때문에, 역시 위 일반항을 이용해 출력한 뒤 또 다음 함수를 호출,
이 과정이 모두 끝나면 다음으로 2에서 3으로 이동하는 함수를 재귀호출하면 된다.
말로 하려니까 꼬이는 감이 있는데, 식으로 보면 훨씬 낫다.
import java.util.Scanner;
public class Prob11729 {
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
sb.append((int)Math.pow(2, n) - 1 + "\n"); // 총 횟수
hanoi(n, 1, 2, 3);
System.out.println(sb);
}
static void hanoi(int n, int start, int mid, int to) {
if (n == 1) {
sb.append(start + " " + to + "\n");
return;
}
hanoi(n - 1, start, to, mid);
sb.append(start + " " + to + "\n");
hanoi(n - 1, mid, start, to);
}
}출발지를 start, 중간을 mid, 목적지를 to로 주었으며
시간제한을 피하기 위해 스트링 빌더를 사용했다.
'Algorithm > [Java+Python+JavaScript]BackJoon' 카테고리의 다른 글
| [BackJoon]14425번 (1) | 2023.01.24 |
|---|---|
| [BackJoon]10815번 (0) | 2023.01.19 |
| [BackJoon]2798번 (0) | 2023.01.17 |
| [BackJoon]2798번 (2) | 2023.01.14 |
| [BackJoon]24060번 (2) | 2023.01.13 |
| [BackJoon]18870번 (4) | 2023.01.02 |
- Total
- Today
- Yesterday
- 여행
- Algorithm
- 스트림
- 리스트
- BOJ
- 파이썬
- 중남미
- 백준
- 유럽여행
- 남미
- 맛집
- 칼이사
- 동적계획법
- 지지
- java
- 세모
- 기술면접
- 자바
- 야경
- 면접 준비
- 세계여행
- Python
- RX100M5
- a6000
- 스프링
- Backjoon
- spring
- 세계일주
- 알고리즘
- 유럽
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

