티스토리 뷰
목차
들어가며
감마 함수는 정수 팩토리얼(n!) 개념을 실수(혹은 복소수) 영역으로 일반화한 함수이다.
확률 분포 이론에서 자주 등장하며, 특히 베타 분포(Beta distribution), 감마 분포(Gamma distribution),
디리클레 분포(Dirichlet distribution) 등에서 중심적인 역할을 한다.
좀 더 구체적으로는 머신러닝을 비롯한 확률론 기반 모델에서는 감마함수를 양의 실수영역까지만 확장해서 사용한다.
당연하다면 당연하게도 음수나 복소수의 경우엔 확률 분포가 성립하지 않거나 정규화 상수가 무의미해지기 때문이다.
정의
양의 실수 z>0에 대해 감마 함수는 다음과 같이 정의된다:
Γ(z)=∫∞0tz−1e−tdt
이는 무한 적분으로 정의되며, z가 양의 정수일 때 다음 성질을 만족한다:
Γ(n)=(n−1)!\quad(\text{for } n∈\mathbb{N})
즉,
- \Gamma(1) = 0! = 1
- \Gamma(2) = 1! = 1
- \Gamma(3) = 2! = 2
- \Gamma(4.5) 같은 경우는 일반적인 팩토리얼로는 정의할 수 없지만 감마 함수를 통해 계산할 수 있다.
왜 이런 모양인가?
이 정의는 다음 조건을 만족해야 한다는 수학적 요구에서 출발했다:
- \Gamma(1) = 1
- \Gamma(z+1) = z \cdot \Gamma(z) (팩토리얼 재귀 성질)
- 적분으로 표현 가능하고, 실수 전체에 대해 정의됨
사실 위 조건은 오일러가 팩토리얼을 확장하는 과정에서 찾았던 조건
- f(1) = 1
- f(z+1) = z \cdot f(z)
- f(z)가 실수 전체에 대해 정의되며, 연속적이고 부드러운 함수여야 함
에서 왔으며, 이 세 조건을 만족하는 함수가 적분 형태로 정의되는 감마 함수 \Gamma(z)밖에 없다는 것이 증명되었다.
증명은.. 여백이 모자라서 생략한다.
그래도 감마 함수가 팩토리얼을 일반화하는 과정은 간단하기 때문에 잠깐 살펴보고 지나가자.
정수 n에 대해 다음을 보자:
\Gamma(n)=\int^\infty_0t^{n-1}e^{-t}dt
n = 1일 때
\Gamma(1)=\int^\infty_0t^{0}e^{-t}dt=\int^\infty_0e^{-t}dt=1
즉, \Gamma(1) = 0!
n = 2일 때
\Gamma(2)=\int^\infty_0t^{1}e^{-t}dt
부분적분하면:
- u = t, dv = e^{-t} dt
- du = dt, v = -e^{-t}
\Gamma(2)=[-te^{-t}]^\infty_0+\int^\infty_0e^{-t}dt=0+1=1=1!
일반화
부분적분을 일반화하면 다음과 같은 결과를 얻는다:
\Gamma(n+1)=\int^\infty_0t^{n}e^{-t}dt=n\cdot\Gamma(n)
따라서
Γ(n)=(n−1)!
즉, 감마 함수는 다음 조건을 만족한다:
- \Gamma(n) = (n-1)! for natural numbers n
- \Gamma(z+1) = z \cdot \Gamma(z) for all z
- \Gamma(1) = 1
주요 성질
재귀 관계 (Recurrence relation)
감마 함수는 다음의 재귀적 성질을 갖는다:
Γ(z+1)=z⋅Γ(z)
이는 팩토리얼의 정의 n! = n \cdot (n-1)!와 동일한 구조이다.
이를 이용해 비정수에 대한 계산도 재귀적으로 진행 가능하다.
\Gamma\left(1/2\right)의 값
감마 함수는 정수 외의 값에서도 정의되며, 특히 다음 결과는 자주 쓰인다:
Γ(\frac{1}{2})= \sqrt{π}
이 결과는 정규분포의 정규화 상수를 유도할 때 결정적인 역할을 한다.
따라서 \pi가 확률분포에 등장하는 이유는 사실상 감마 함수 때문이다.
\Gamma(n)은 (n-1)!
이 결과를 직관적으로 이해하면 다음과 같다:
Γ(n)=(n-1)! \quad n \in \mathbb{N}
베타 분포에서 자주 등장하는 분모
\frac{\Gamma[\alpha + \beta]}{\Gamma[\alpha] \Gamma[\beta]}
는 일반적인 이항 계수(binomial coefficient)와 유사한 구조를 가지며, 베이즈 추론에서 정규화 상수로 활용된다.
그래프
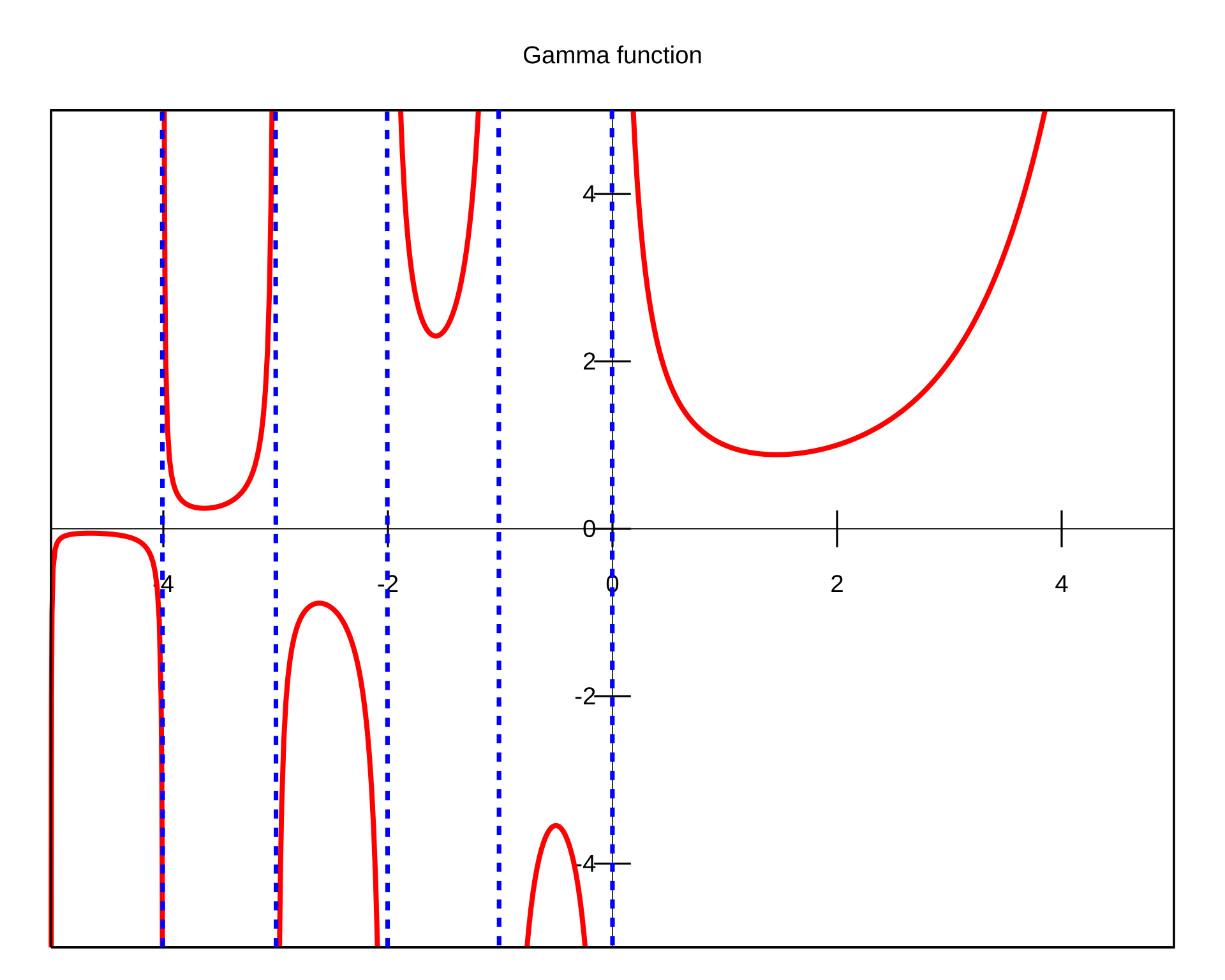
감마 함수의 그래프는 다음과 같은 특징을 가진다:
- z = 1, 2, 3, \dots에서는 점점 커지며 발산
- z \in (0,1)에서는 \Gamma(z) > 1
- z = 0, -1, -2, \dots에서는 정의되지 않으며 극점(pole)이 존재
따라서 감마 함수는 음의 정수에서는 정의되지 않음에 주의해야 한다.
감마 함수 & 베타 함수
베타 함수(Beta function)는 감마 함수와 밀접한 관련이 있으며 다음과 같은 식으로 연결된다:
B(α,β) = \int^1_0t^{α-1}(1-t)^{β-1}dt = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)}
즉, 베타 분포의 분모에 등장하는 \Gamma 항들은 베타 함수의 정규화 상수를 구성하는 요소이다.
요약
- 감마 함수는 n!을 실수 영역으로 확장한 함수이다.
- \Gamma(n) = (n-1)!이며, \Gamma(1/2) = \sqrt{\pi}이다.
- 베타/감마/디리클레 분포 등에서 자주 사용된다.
- 정규화 상수로 자주 등장하며, 분포의 모양을 수학적으로 정리하는 데 필수적이다.
- 실수 및 복소수에서도 정의되며 재귀성과 정적분으로 계산 가능하다.
'ML+DL > Computer Vision By Simon J.D. Prince' 카테고리의 다른 글
| Chapter 3: Common Probability Distributions (0) | 2025.04.03 |
|---|---|
| 확률 모델의 불확실성? 베이지안 관점에서의 하이퍼파라미터 (0) | 2025.03.25 |
| 확률 밀도 함수(Probability Density Function, pdf) (0) | 2025.03.25 |
| Chapter 2: Introduction to probability (0) | 2025.03.21 |
| 베이즈 정리(Bayes' theorem) (0) | 2025.03.21 |
| Part I: Probability (0) | 2025.03.19 |
- Total
- Today
- Yesterday
- BOJ
- 파이썬
- 세계일주
- 동적계획법
- Algorithm
- 야경
- 유럽여행
- 스트림
- 유럽
- 맛집
- 기술면접
- 중남미
- 세계여행
- 리스트
- 칼이사
- 세모
- Backjoon
- spring
- RX100M5
- 지지
- 남미
- 면접 준비
- 백준
- 자바
- 알고리즘
- 여행
- 스프링
- java
- Python
- a6000
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

