Chapter 3: Common Probability Distributions

목차

• 서론
• 3.1 베르누이 분포 (Bernoulli Distribution)
  • 요약
• 3.2 베타 분포 (Beta Distribution)
  • 베타분포의 성질 요약
  • 핵심 요약
• 3.3 범주형 분포 (Categorical Distribution)
  • 확률 벡터 표현
  • 수식 표현
  • 단위 벡터 표현 (One-hot encoding 관점)
  • 핵심 요약
• 3.4 디리클레 분포 (Dirichlet distribution)
  • 디리클레 분포의 정의
  • 베타 분포와의 관계
  • 핵심 요약
• 3.5 단변량 정규 분포 (Univariate Normal Distribution)
  • 핵심 요약
• 3.6 정규-스케일드 역감마 분포 (Normal-scaled Inverse Gamma Distribution)
  • 좀 더 구체적으로 설명하자면
  • 왜 정규-스케일드 역감마 분포를 쓰는가?
  • 요약
  • 핵심 요약
• 3.7 다변량 정규 분포 (Multivariate Normal Distribution)
  • 분포의 구성 요소
  • 확률 밀도 함수 (Probability Density Function)
  • 중요성
• 3.8 정규-역 위샤트 분포 (Normal Inverse Wishart Distribution)
  • 핵심 요약
  • 추가: 공분산(covariance)
    • 공분산의 해석
    • 공분산과 공분산 행렬
    • 예시로 보는 공분산
    • 정리
• 3.9 켤레성 (Conjugacy) - 켤레로 관련된 그룹의 두 요소 간의 관계
  • 켤레 관계의 중요성
  • 핵심 요약
  • 추가: 켤레 분포는 ‘형태를 보존’하는 사전 분포다
    • 켤레성과 고윳값의 유사성
    • 켤레 분포에서의 \kappa(x, \alpha, \beta)\kappa(x, \alpha, \beta): 정규화 상수 (Normalization Constant)
    • 왜 켤레 분포가 중요한가?
    • 예시 다시 보기: 베르누이 + 베타
    • 정리: 켤레 분포는 “분포 공간의 고유 구조”
• 요약

 

서론

 

2장에서 확률을 조작하는 추상적인 규칙들을 소개했다.

 

이러한 규칙들을 실제로 사용하려면, 먼저 구체적인 확률 분포를 정의해야 한다.

 

어떤 확률 분포 $Pr(x)$를 사용할지는 우리가 모델링하고자 하는 데이터 $x$의 도메인(domain)에 따라 달라진다.

 

표 3.1은 다양한 데이터 유형과 그에 대응하는 대표적인 확률 분포들을 정리한 것이다.

 

여기서 도메인이란 정의역(domain of definition)에서의 도메인이며,

 

이 경우에는 확률 변수 $x$가 가질 수 있는 값들의 집합, 즉 확률 분포 $Pr(x)$가 정의되는 값의 종류와 범위를 의미한다.

 

데이터 유형	도메인 $x$	분포 이름
단변량, 이산형, 이진(binary)	$x \in {0, 1}$	베르누이 분포 (Bernoulli)
단변량, 이산형, 다중 값	$x \in {1, 2, ..., K}$	범주형 분포 (Categorical)
단변량, 연속형, 무한 범위	$x \in \mathbb{R}$	단변량 정규 분포 (Univariate Normal)
단변량, 연속형, [0, 1]로 제한	$x \in [0,1]$	베타 분포 (Beta)
다변량, 연속형, 무한 범위	$x \in \mathbb{R}^K$	다변량 정규 분포 (Multivariate Normal)
다변량, 연속형, [0,1]로 제한, 합이 1	$x=[x_1,x_2,...x_K]^T$ $x_k \in [0,1]$, $\sum_{k=1}^{K} x_k = 1$	디리클레 분포 (Dirichlet)
이변량, 연속형, $x_1$은 무한, $x_2$는 0 이상	$x = [x_1, x_2]^T$, $x_1 \in \mathbb{R}$, $x_2 \in \mathbb{R}^+$	정규-스케일 역감마 분포 (Normal-scaled Inverse Gamma)
벡터 $x$와 행렬 $X$, $x$는 무한 범위, $X$는 양의 정부호 정사각 행렬	$x \in \mathbb{R}^K$, $X \in \mathbb{R}^{K \times K}$, $\forall z \in \mathbb{R}^K, z^T X z > 0$	정규-역위샤트 분포 (Normal-Inverse Wishart)

표 3.1: 모델링할 데이터의 유형(예: 이산/연속, 단변량/다변량 등)에 따라 어떤 확률 분포를 사용하는 것이 적절한지를 요약한 표. 각 분포는 해당 도메인에 최적화된 수학적 성질을 가지며, 실제 알고리즘에서 자주 사용된다.

 

시각 데이터를 모델링할 때 범주형(categorical) 분포나 정규(normal) 분포 같은 확률 분포는 명백히 유용하다. 

 

하지만 그 외의 분포들이 왜 필요한지는 처음에는 직관적으로 이해되지 않을 수 있다. 

 

예를 들어, 디리클레(Dirichlet) 분포는 합이 1인 양수 K개를 모델링하는데, 

 

시각 데이터는 일반적으로 이러한 형태를 띠지 않는다.

 

이러한 분포가 필요한 이유는 다음과 같다. 

 

데이터를 대상으로 확률 모델을 적합(fit)할 때, 우리는 그 적합의 불확실성도 알고 있어야 한다. 

 

이 불확실성은 적합된 모델의 파라미터(parameter) 위에 정의된 또 하나의 확률 분포로 표현된다. 

 

즉, 어떤 분포를 사용하여 데이터를 모델링할 때, 

 

그 분포에 쓰인 파라미터 자체에 대한 이차적(second-order) 확률 분포가 존재한다. 이 내용을 표 3.2에 요약하였다.

 

분포 (Distribution)	정의역 (Domain)	파라미터를 모델링하는 분포 (Modeled by)
베르누이(Bernoulli)	$x \in {0, 1}$	베타(Beta)
범주형(Categorical)	$x \in {1, 2, ..., K}$	디리클레(Dirichlet)
단변량 정규(Univariate normal)	$x \in \mathbb{R}$	정규-역감마(Normal Inverse Gamma)
다변량 정규(Multivariate normal)	$x \in \mathbb{R}^k$	정규-역위샤트(Normal Inverse Wishart)

표 3.2: 왼쪽 열: 데이터 모델링에 사용되는 주요 분포들. 가운데 열: 각 분포가 정의되는 값의 영역. 오른쪽 열: 해당 분포의 파라미터를 모델링하는 이차 확률 분포.

 

(이 표는 하나의 핵심 개념을 강조한다: 어떤 데이터를 모델링할 때 사용하는 확률 분포뿐 아니라, 그 파라미터에 대한 불확실성까지 모델링하는 분포도 함께 고려해야 한다. 이는 특히 베이지안 추론(Bayesian inference)에서 핵심적인 사고 방식이다.)

 

예를 들어, 디리클레 분포는 범주형 분포의 파라미터를 모델링하는 데 사용된다. 

 

이 맥락에서 디리클레 분포의 파라미터들은 하이퍼파라미터(hyperparameter)라고 불린다. 

 

보다 일반적으로, 하이퍼파라미터는 원래 분포의 파라미터에 대한 분포의 형태를 결정하는 역할을 한다.

 

확률 모델의 불확실성? 베이지안 관점에서의 하이퍼파라미터

확률 모델의 불확실성? 베이지안 관점에서의 하이퍼파라미터

 

이제 표 3.2에 제시된 분포들을 하나씩 살펴본 뒤, 이러한 분포 쌍들 간의 관계를 자세히 살펴볼 것이다.

 

3.1 베르누이 분포 (Bernoulli Distribution)

그림 3.1 베르누이 분포는 $x \in {0, 1}$의 두 가지 결과만을 가지는 이산 분포이다. 이때 0은 "실패", 1은 "성공"으로 간주한다. 단일 파라미터 $\lambda$에 의해 정의되며, 이는 $x=1$이 될 확률이다. $Pr(x=0) = 1 - \lambda$, $Pr(x=1) = \lambda$로 표현된다.

 

베르누이 분포는 단 하나의 파라미터 $\lambda \in [0,1]$를 가지며, 이는 성공($x=1$)이 일어날 확률을 나타낸다.

베르누이 분포는 다음과 같이 정의된다:

 

$$\begin{align*} Pr(x=0) &= 1−λ \\ Pr(x=1) &= λ \end{align*}\tag{3.1}$$

 

또는 이를 하나의 수식으로 결합하면 다음과 같이 표현할 수 있다:

 

$$Pr(x)=λ^x(1-λ)^{1-x}\tag{3.2}$$

 

이 표현은 $x$가 0 또는 1이라는 특성을 이용한 것이다. 

 

예를 들어, $x = 1$일 때는 $Pr(1) = \lambda$, $x = 0$일 때는 $Pr(0) = 1 - \lambda$가 된다.

 

때때로 다음과 같은 축약된 표기법을 사용하기도 한다:

 

$$Pr(x)=\text{Bern}_x[λ]\tag{3.3}$$

 

이는 "확률 변수 $x$가 파라미터 $\lambda$를 갖는 베르누이 분포를 따른다"는 의미이다.

 

요약

• 두 가지 결과(0 또는 1)만을 가지는 확률 변수의 분포를 모델링한다.
• 단 하나의 파라미터 $\lambda$로 결정되며, 이는 $x=1$이 될 확률이다.
• 베르누이 분포는 머신 비전에서 픽셀 이진 상태, 객체 존재 유무 등 다양한 이진 상태를 모델링하는 데 사용된다.

3.2 베타 분포 (Beta Distribution)

그림 3.2 베타 분포: 베타 분포는 구간 $[0,1]$ 위에 정의되며, 매개변수 $(\alpha, \beta)$의 상대적 크기가 기댓값 $E[\lambda]$를 결정한다. 각 곡선 옆의 괄호 속 숫자는 해당 곡선의 $(\alpha, \beta)$ 값을 의미한다. (a) 모든 곡선에서 $E[\lambda] = 0.5$. 하지만 $(\alpha, \beta)$의 절댓값이 커질수록 평균 주변의 <집중도>가 증가한다. (b) $E[\lambda] = 0.25$인 경우. 즉, $\alpha < \beta$인 상황. (c) $E[\lambda] = 0.75$인 경우. 즉, $\alpha > \beta$인 상황.

베타 분포는 연속 확률 분포이며, 단일 변수 $\lambda$에 대해 정의되며 $\lambda \in [0,1]$ 범위를 갖는다. 

 

따라서 베르누이 분포(Bernoulli distribution)의 파라미터 $\lambda$에 대한 불확실성을 표현하는 데 적합하다.

 

베타 분포는 두 개의 양의 실수 매개변수 $\alpha, \beta \in (0, \infty)$를 가지며, 

 

이 매개변수들은 곡선의 형태(shape)에 영향을 준다. 그림 3.2는 다양한 $(\alpha, \beta)$ 값에 따른 분포의 변화를 보여준다.

 

수학적으로, 베타 분포는 다음과 같은 형태를 갖는다:

 

$$Pr(λ)=\frac{\Gamma[\alpha+\beta]}{\Gamma[\alpha]\Gamma[\beta]}λ^{\alpha-1}(1-λ)^{\beta-1}\tag{3.4}$$

 

여기서 $\Gamma[\cdot]$는 감마 함수(gamma function)를 나타낸다. 간단히 표기할 때는 다음과 같이 쓴다:

 

$$Pr(λ)=\text{Beta}_λ[\alpha,\beta]\tag{3.5}$$

 

감마 함수 (Gamma Function)

감마 함수 (Gamma Function)

 

베타분포의 성질 요약

• 정의역: $\lambda \in [0,1]$
• 매개변수: $\alpha > 0$, $\beta > 0$
• 기댓값(평균): 여기서 기댓값(평균)이라고 적은 이유는 베타 분포에서는 함수 $f[\cdot]$가 그냥 변수 자체이기 때문이다.

$$E[λ]=\frac{\alpha}{\alpha+\beta}$$

 

• 매개변수의 비율은 분포의 중심을 결정하며, 절댓값은 곡선의 집중도(concentration)를 조절한다.

핵심 요약

• 베타 분포는 확률값 또는 확률 파라미터의 불확실성을 표현하는 데 널리 사용된다.
• 특히, 베르누이 및 이항 분포의 파라미터 $\lambda$에 대한 사전 분포(prior)로 자주 쓰인다.
• $\alpha$와 $\beta$의 상대적인 크기는 기댓값 $E[\lambda]$를, 절댓값은 분포의 확신의 정도(신뢰도)를 나타낸다.
• 베타 분포는 사후 분포(posterior)를 해석하거나 베이즈 추론에서 핵심적인 역할을 한다.

3.3 범주형 분포 (Categorical Distribution)

그림 3.3 범주형 분포는 $K$개의 가능한 결과 $x \in {1,2,...,K}$를 갖는 이산 분포이며, 각 결과에 대응하는 확률 $\lambda_1, \lambda_2, ..., \lambda_K$를 가진다. 각 $\lambda_k$는 0 이상이며 전체 합은 1이다. $x = k$가 발생할 확률은 $\lambda_k$이다. 가능한 결과의 수 $K=2$일 경우, 이 분포는 베르누이 분포로 특수화된다.

범주형 분포(categorical distribution)는 $K$개의 가능한 결과 중 

 

하나가 관측될 확률을 정의하는 이산 확률 분포이다 (그림 3.3 참조). 

 

$K=2$인 경우에는 이 분포가 베르누이 분포(Bernoulli distribution)로 특수화된다.

 

컴퓨터 비전에서 픽셀의 밝기(intensity) 데이터는 일반적으로 

 

이산적인 수준(discrete levels)으로 양자화되므로, 범주형 분포로 모델링할 수 있다. 

 

또한, 세계의 상태 역시 여러 개의 이산적인 값 중 하나일 수 있다. 

 

예를 들어, 어떤 차량 이미지가 주어졌을 때, 이를 {car, motorbike, van, truck} 중 하나로 분류한다고 하자. 

 

이 상태에 대한 불확실성 역시 범주형 분포로 표현할 수 있다.

 

확률 벡터 표현

 

$K$개의 결과에 대한 확률은 다음과 같은 <$K \times 1$ 차원의 파라미터 벡터> 

 

$\lambda = [\lambda_1, \lambda_2, ..., \lambda_K]$에 저장된다. 

 

각 파라미터는 다음 조건을 만족한다:

 

• $\lambda_k \in [0,1]$
• $\sum_{k=1}^{K} \lambda_k = 1$

즉, 각각의 $\lambda_k$는 <결과 $k$가 관측될 확률>을 나타낸다.

 

수식 표현

 

범주형 분포는 정규화된 히스토그램으로 시각화할 수 있으며, 

 

확률 변수 $x$가 값 $k$를 가질 확률은 다음과 같이 표현된다:

 

$$Pr(x=k)=λ_k\tag{3.6}$$

 

간단하게는 아래와 같은 표기법을 사용할 수 있다:

 

$$Pr(x)=\text{Cat}_x[λ]\tag{3.7}$$

 

단위 벡터 표현 (One-hot encoding 관점)

 

또 다른 방식으로는, 데이터 $x$를 $x \in {e_1, e_2, ..., e_K}$의 값 중 하나를 가진다고 생각할 수 있다. 

 

여기서 $e_k$는 단위 벡터(unit vector)이며, $k$번째 요소만 1이고 나머지는 모두 0이다.

 

이 표현을 사용하면, 범주형 분포는 다음과 같이 쓸 수 있다:

 

$$Pr(x=e_k)= \prod_{j=1}^{K}λ _j^{x_j} =λ_k\tag{3.8}$$

 

여기서 $x_j$는 벡터 $x$의 $j$번째 요소이다.

 

이 표현은 추후 다변량 확률 분포에서 지수 형태의 표현과 연결되며, 범주형 변수의 연산적 표현에 유용하다.

 

핵심 요약

• 범주형 분포는 $K$개의 이산 결과 중 하나가 관측될 확률을 정의한다.
• 베르누이 분포는 $K=2$일 때의 특수한 경우이다.
• 파라미터 벡터 $\lambda$는 각 결과의 확률을 포함하며, 총합은 1이다.
• 확률은 스칼라 값($x = k$) 또는 단위 벡터($x = e_k$) 관점에서 표현될 수 있다.

3.4 디리클레 분포 (Dirichlet distribution)

그림 3.4 디리클레 분포의 시각화. (a) $K=3$일 때, 디리클레 분포는 $\sum_k \lambda_k = 1$을 만족하는 삼각형 영역 위에서 정의된다. (b–e)에서는 $\alpha$들의 비율은 동일하게 유지하되, 그 절대값을 증가시키는 경우를 보여준다. → 이 경우, 분포는 점점 더 중심(기댓값) 주위로 <날카롭게 집중>된다. (f–i)에서는 $\alpha_3 > \alpha_2 > \alpha_1$와 같이 <비율을 변화>시키고, 동시에 절대값도 증가시킨다. → 이 경우, 분포는 $\lambda_3$ 쪽에 더 큰 값을 부여하고, 점차적으로 집중된다.

디리클레 분포(Dirichlet distribution)는 그림 3.4와 같이 

 

$K$개의 연속적인 값 $\lambda_1, \dots, \lambda_K$에 대해 정의된다. 

 

각 성분은 $0$과 $1$ 사이의 값을 가지며, 다음의 제약 조건을 만족해야 한다:

 

$$\sum_{k=1}^{K}\lambda_k=1,\quad\lambda_k\in[0,1]$$

 

따라서 디리클레 분포는 범주형 분포(categorical distribution)의 파라미터들에 대한 분포를 정의하는 데 적합하다. 

 

즉, 범주형 분포의 확률 파라미터들에 대한 확률 분포로 사용된다.

 

디리클레 분포의 정의

 

$K$차원 디리클레 분포는 $K$개의 양의 실수 매개변수 $\alpha_1, \dots, \alpha_K$로 정의된다.

 

• 이 비율은 기댓값 $E[\lambda_1], \dots, E[\lambda_K]$을 결정하고,
• 이 크기는 기댓값 주변으로의 집중 정도(concentration)를 결정한다.

즉, $\alpha$들의 비율은 분포가 어디에 중심을 두는지를 결정하고, 

 

$\alpha$들의 절댓값은 분포가 얼마나 좁게 집중되는지를 결정한다.

 

분포의 확률 밀도 함수는 다음과 같이 정의된다:

 

$$Pr(λ_1,...,λ_k)=\frac{Γ(\sum_{k=1}^K\alpha_k)}{∏_{k=1}^KΓ(\alpha_k)}\prod_{k=1}^{K}λ _k^{\alpha_k-1}\tag{3.9}$$

 

또는 간단하게:

 

$$Pr(λ_1,...,λ_k)=\text{Dir}_{\lambda_{1...k}}[\alpha_1,...,\alpha_K]\tag{3.10}$$

 

여기서 $\Gamma[\cdot]$는 감마 함수(gamma function)를 의미한다. 

 

감마 함수는 정수 $n$에 대해 $\Gamma(n) = (n-1)!$과 같다.

 

베타 분포와의 관계

 

베르누이 분포(Bernoulli distribution)가 범주형 분포(categorical distribution)의 특수한 경우였던 것처럼,

 

베타 분포(Beta distribution)는 디리클레 분포의 특수한 경우이다.

 

즉, 차원이 2일 때의 디리클레 분포가 바로 베타 분포이다.

 

핵심 요약

• 디리클레 분포는 확률 벡터 $(\lambda_1, \dots, \lambda_K)$에 대한 확률 분포이다.
• 각 성분은 $[0,1]$ 사이이며 전체 합이 1이다.
• 파라미터 $\alpha_k$는 분포의 형태와 집중 정도를 결정한다.
• 베타 분포는 디리클레 분포의 2차원 특수 사례이다.
• 머신러닝에서는 분류 문제의 파라미터 추론, 베이지안 모델링, 잠재 디리클레 할당(LDA) 등의 맥락에서 자주 등장한다.

3.5 단변량 정규 분포 (Univariate Normal Distribution)

그림 3.5 단변량 정규 분포는 $x \in \mathbb{R}$에 정의되며, 두 파라미터 ${\mu, \sigma^2}$를 가진다. 평균 $\mu$는 기댓값을 결정하고, 분산 $\sigma^2$는 평균 주위의 집중도를 결정한다. $\sigma^2$가 커질수록 분포는 더 넓고 평평해진다.

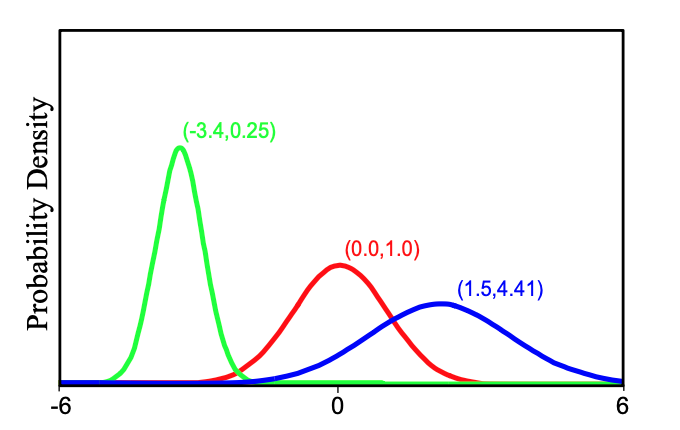
단변량 정규 분포 또는 가우시안 분포는 연속적인 실수 값 $x \in (-\infty, \infty)$ 위에 정의된다.

 

컴퓨터 비전에서는 종종 픽셀의 강도가 이산적인 값(quantized)이라는 사실을 무시하고, 

 

이를 연속적인 정규 분포로 모델링한다.

 

또한, 세상의 상태 자체도 정규 분포로 설명할 수 있다. 

 

예를 들어, 어떤 물체까지의 거리를 정규 분포로 나타낼 수 있다.

 

정규 분포는 두 개의 파라미터, 즉 평균 $\mu$와 분산 $\sigma^2$을 가진다.

 

• 평균 $\mu$는 분포의 중심 위치를 결정하며, 실수 전체에서 어떤 값이든 취할 수 있다.
• 분산 $\sigma^2$는 분포의 폭을 조절하며, 양의 실수만 가능하다. 분산이 클수록 분포는 더 넓고 평평해진다.

정규 분포의 확률 밀도 함수는 다음과 같이 정의된다:

 

$$Pr(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\text{exp}(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2})\tag{3.11}$$

 

보다 간단히 다음과 같이 표기한다:

 

$$Pr(x)=\text{Norm}_x[\mu,\sigma^2]\tag{3.12}$$

 

핵심 요약

• 정규 분포는 연속 확률 변수에 대한 가장 널리 사용되는 분포 중 하나이다.
• 평균 $\mu$는 기댓값(expected value)이며 분포의 중심을 결정한다.
• 분산 $\sigma^2$는 퍼짐의 정도를 나타내며, 값이 커질수록 분포는 넓어지고 평평해진다.
• 픽셀 강도, 거리와 같은 물리적 속성도 정규 분포로 모델링 가능하다.

3.6 정규-스케일드 역감마 분포 (Normal-scaled Inverse Gamma Distribution)

 

Base parameters: [α,β,γ,δ] = [1,1,1,0], The normal-scaled inverse gamma distribution is a bivariate distribution over (μ,σ²) where μ∈[−∞,∞] and σ²∈[0,∞].

정규-스케일드 역감마 분포(normal-scaled inverse gamma distribution)는 

 

두 개의 연속 값 $(\mu, \sigma^2)$에 대해 정의되는 분포이다.

 

여기서 $\mu$는 실수 전체 범위의 값을 가질 수 있고, $\sigma^2$는 양의 실수로 제한된다. 

 

이 분포는 곧 정규 분포의 평균과 분산에 대한 확률 분포를 정의하는 데 적합하다.

 

좀 더 구체적으로 설명하자면

 

정규-스케일드 역감마 분포(Normal-scaled inverse gamma distribution)는 

 

정규 분포의 평균 $\mu$와 분산 $\sigma^2$에 대한 하이퍼파라미터(하이퍼파라미터) 분포, 

 

즉 사전 분포(prior distribution) 역할을 한다.

 

우리가 어떤 데이터 $x$가 정규 분포 $\mathcal{N}(\mu, \sigma^2)$를 따른다고 가정하고,

이때 $\mu$와 $\sigma^2$ 모두 모르는 값이어서 추정하고 싶다고 하자.

이 경우 베이지안 접근법에서는 $\mu$와 $\sigma^2$ 자체를 확률 변수로 보고,

 

이들에 대해 사전 분포 $Pr(\mu, \sigma^2)$를 설정한다.

바로 이때 사용할 수 있는 것이 정규-스케일드 역감마 분포이다.

 

왜 정규-스케일드 역감마 분포를 쓰는가?

 

이 분포는 다음의 성질을 만족한다:

 

• $\mu$는 $\sigma^2$에 조건부로 정규 분포를 따르고:
  $Pr(\mu | \sigma^2) = \mathcal{N}(\delta, \sigma^2 / \gamma)$
• $\sigma^2$는 역감마 분포를 따른다:
  $Pr(\sigma^2) = \text{Inv-Gamma}(\alpha, \beta)$

이 구조는 수학적으로 매우 다루기 쉬운데, 이유는 다음과 같다:

 

정규 분포와 정규-스케일드 역감마 분포는 서로 conjugate하다.

 

즉, 데이터가 정규 분포를 따른다고 가정하고,

 

사전 분포로 정규-스케일드 역감마를 설정하면,

 

사후 분포도 동일한 형태(정규-스케일드 역감마)를 유지하게 된다.

 

이것이 바로 베이지안 추론에서 이상적인 구조이다.

 

요약

• 정규-스케일드 역감마 분포는 정규 분포의 평균 $\mu$와 분산 $\sigma^2$에 대한 사전 분포이다.
• 베이지안 정규 추정 문제에서 자주 사용된다.
• $\mu$는 $\sigma^2$에 조건부로 정규 분포를 따르고, $\sigma^2$는 역감마 분포를 따름.
• 이 구조는 계산적으로 깔끔하고 사후 분포 형태가 유지되는 conjugate prior이다.
  
  

---

다시 돌아와서, 이 분포는 네 개의 매개변수 $\alpha$, $\beta$, $\gamma$, $\delta$를 가진다. 

 

이 중에서 $\alpha$, $\beta$, $\gamma$는 양의 실수이며, $\delta$는 실수 전체 범위를 가질 수 있다.

정규-스케일드 역감마 분포의 확률 밀도 함수(pdf)는 다음과 같이 정의된다:

 

$$Pr(μ,σ^2)=\sqrt{\frac{γ}{2π}}⋅\frac{β^α}{Γ[α]}⋅\frac{1}{σ^{2(α+1)}}⋅\text{exp}(-\frac{2β+γ(δ−μ)^2}{2σ^2})\tag{3.13}$$

 

또는 간략한 표기법으로 다음과 같이 쓸 수 있다:

 

$$Pr(μ,σ^2)=\text{NormInvGam}_{μ,σ^2}[α,β,γ,δ]\tag{3.14}$$

 

이 분포는 주로 정규 분포의 평균 $\mu$와 분산 $\sigma^2$를 함께 추론할 때 사용되며, 

 

특히 베이지안 추론에서 conjugate prior로 자주 등장한다. 

 

직관적으로는, 평균 $\mu$는 $\delta$를 중심으로 정규 분포를 따르고, 

 

분산 $\sigma^2$는 감마 분포의 역수 형태를 따르며, 이 둘이 함께 결합된 구조를 가진다.

 

핵심 요약

• 이 분포는 두 변수 $\mu$, $\sigma^2$에 대한 결합 확률 분포이다.
• $\mu$는 실수 전체 범위, $\sigma^2$는 양의 실수만 가능하다.
• $\alpha$, $\beta$, $\gamma$는 양의 실수, $\delta$는 실수.
• 주로 정규 분포의 평균과 분산에 대한 베이지안 추론에서 사용된다.
• $\mu$와 $\sigma^2$의 동시 분포를 모델링할 수 있다는 점에서 유용하다.

3.7 다변량 정규 분포 (Multivariate Normal Distribution)

 

그림 3.7 다변량 정규 분포는 $x = [x_1, \dots, x_D]^T$와 같이 $D$차원의 연속적인 실수 벡터를 모델링한다. 이 분포는 평균을 나타내는 $D \times 1$ 벡터 $\boldsymbol{\mu}$와 분포의 형상을 결정하는 $D \times D$ 공분산 행렬 $\boldsymbol{\Sigma}$로 정의된다. 이 분포의 등확률 곡선(iso-contours)은 <타원체(ellipsoid)>이며, 타원의 중심은 평균 $\boldsymbol{\mu}$에 의해 결정되고, 타원의 크기와 기울기, 방향은 공분산 행렬 $\boldsymbol{\Sigma}$에 의해 결정된다. 이 그림에서는 2차원 이변량 정규 분포(bivariate distribution)를 묘사하고 있으며, 공분산 구조를 설명하기 위해 하나의 타원체를 시각적으로 표현하였다.

다변량 정규 분포 또는 다변량 가우시안 분포는 $D$차원 변수 $\mathbf{x}$를 모델링하며, 

 

이때 각 요소 $x_1, \dots, x_D$는 모두 연속적이고 정의역이 $[-\infty, +\infty]$ 전 구간에 걸친다 (그림 3.7 참조).

 

단변량 정규 분포(univariate normal distribution)는 이 다변량 정규 분포의 특수한 경우로, 차원 수 $D$가 1일 때 해당한다.

머신 비전에서는 다변량 정규 분포를 이용하여 이미지의 특정 영역 내에 존재하는 

 

픽셀 $D$개의 명암 값의 결합 분포(joint distribution)를 모델링할 수 있다.

 

또한, 세상 상태의 불확실성을 이 분포로 기술할 수도 있다. 

 

예를 들어, 다변량 정규 분포는 장면(scene) 내 객체의 3차원 위치 $(x, y, z)$에 대한 결합적인 불확실성을 표현할 수 있다.

 

분포의 구성 요소

 

다변량 정규 분포는 두 개의 파라미터(parameter)로 구성된다:

 

1. 평균 벡터 $\boldsymbol{\mu}$:
   $D \times 1$ 크기의 벡터로, 각 차원의 평균값을 나타낸다.
2. 공분산 행렬 $\boldsymbol{\Sigma}$:
   $D \times D$ 크기의 대칭(symmetric), 양의 정부호(positive definite) 행렬이다.
   즉, 임의의 실수 벡터 $\mathbf{z}$에 대해 $\mathbf{z}^T \boldsymbol{\Sigma} \mathbf{z} > 0$을 만족해야 한다.
   이 행렬은 각 차원 간의 분산(자기 자신과의 관계)과 공분산(다른 차원과의 관계)을 동시에 담고 있다.

확률 밀도 함수 (Probability Density Function)

 

다변량 정규 분포의 확률 밀도 함수는 다음과 같이 정의된다:

 

$$Pr(x)=\frac{1}{(2π)^{D/2}|Σ|^{1/2}}\text{exp}(-\frac{1}{2}(x−μ)^TΣ^{-1}(x−μ))\tag{3.15}$$

 

 

또는 간단히 다음과 같이 표기할 수 있다:

 

$$Pr(x)=\text{Norm}_x[μ,Σ]\tag{3.16}$$

 

중요성

 

다변량 정규 분포는 이 책 전반에 걸쳐 광범위하게 사용될 예정이다.

 

따라서 제5장에서 이 분포의 다양한 성질과 활용법에 대해 전면적으로 다룬다.

 

3.8 정규-역 위샤트 분포 (Normal Inverse Wishart Distribution)

 

정규-역 위샤트 분포(normal inverse Wishart distribution)는 

 

$D \times 1$ 벡터 $\mu$와 $D \times D$의 양의 정부호 행렬 $\Sigma$에 대한 분포를 정의한다. 

 

따라서 이는 다변량 정규 분포의 파라미터에 대한 불확실성을 기술하는 데 적합하다.

 

그러니까 위의 분포와 비유하자면 다음과 같은 표를 그릴 수 있다는 뜻이다:

분포 종류	하이퍼파라미터 분포
정규분포 (Univariate)	Normal-scaled inverse gamma (NSIG)
다변량 정규분포 (Multivariate)	Normal-inverse Wishart (NIW)

 

정규-역 위샤트 분포는 네 개의 파라미터 $\alpha$, $\Psi$, $\gamma$, $\delta$를 가진다.

 

• $\alpha$와 $\gamma$는 양의 스칼라,
• $\delta$는 $D \times 1$ 벡터,
• $\Psi$는 양의 정부호 $D \times D$ 행렬이다.

이 분포는 다음과 같이 정의된다:

 

$$Pr(μ,Σ)=\frac{γ^{D/2}∣Ψ∣^{α/2}\text{exp}(-0.5Tr[ΨΣ^{-1}]+γ(μ−δ)^TΣ^{-1}(μ−δ))}{2^{αD/2}(2π)^{D/2}∣Σ∣^{(α+D+2)/2}Γ_D[α/2]}\tag{3.17}$$

 

 

여기서, $\Gamma_D[\cdot]$는 다변량 감마 함수(multi-variate gamma function)를 의미하며, 

 

$\text{Tr}[\Psi]$는 행렬 $\Psi$의 trace (대각 성분의 합)를 나타낸다.

표기 간략화를 위해 다음과 같이 쓴다:

 

$$Pr(μ,Σ)=\text{NorIWis}_{μ,Σ}[α,Ψ,γ,δ]\tag{3.18}$$

 

수학적으로 보면 정규-역 Wishart 분포의 형태는 매우 복잡하고 불투명하게 보인다. 

 

그러나 본질적으로 이 함수는 유효한 평균 벡터 $\mu$와 공분산 행렬 $\Sigma$에 대해 양의 값을 출력하는 함수이며, 

 

모든 가능한 $\mu$, $\Sigma$에 대해 적분하면 그 값은 1이 된다.

이 분포는 시각화하기는 어렵지만, 샘플링은 매우 쉽다. 

 

샘플 하나는 정규 분포 하나의 평균과 공분산 쌍을 구성한다. 그림 3.8은 이에 대한 예시를 보여준다.

 

그림 3.8 2차원 정규-역 Wishart 분포로부터의 샘플링. a) 각 샘플은 평균 벡터와 공분산 행렬로 구성되며, 여기서는 해당 가우시안의 Mahalanobis 거리 상에서 일정 밀도 수준을 유지하는 등확률 곡선(iso-contour)을 타원 형태로 시각화하였다. b) $\alpha$를 변화시키면, 관측되는 공분산의 <분산 정도>가 변한다. c) $\Psi$를 변경하면, 평균적인 공분산의 크기 및 형태가 바뀐다. d) $\gamma$를 변경하면, 평균 벡터들이 얼마나 퍼져 있는지, 즉 <평균의 분산>이 조절된다. e) $\delta$를 바꾸면, 평균 벡터의 <중심 위치>가 달라진다.

 

핵심 요약

• 정규-역 Wishart 분포는 다변량 정규 분포의 파라미터 $(\mu, \Sigma)$에 대한 불확실성을 모델링한다.
• 이 분포는 베이지안 추론에서 사전 분포(prior)로 자주 사용된다.
• 파라미터 $(\alpha, \Psi, \gamma, \delta)$는 각각 공분산 및 평균의 중심과 산포를 제어하는 역할을 한다.
• 시각화는 어렵지만, 샘플링을 통해 분포의 특성을 이해할 수 있으며, 특히 Gaussian mixture 모델 등의 베이지안적 확장에서 중요한 역할을 한다.

추가: 공분산(covariance)

 

공분산(covariance)은 두 확률 변수 간의 상관관계를 수치적으로 나타내는 지표이다. 

 

아주 단순하게 말하면, 하나의 값이 커질 때 다른 값도 함께 커지는 경향이 있는지를 측정하는 것이다.

 

두 확률 변수 $x$, $y$에 대해, 공분산은 다음과 같이 정의된다:

 

$$Cov(x,y)=E[(x−μ_x)(y-μ_y)]$$

 

여기서:

 

• $E[\cdot]$는 기댓값 (expectation)
• $\mu_x = E[x]$, $\mu_y = E[y]$는 각각의 평균

공분산의 해석

공분산 값	해석
$\text{Cov}(x, y) > 0$	$x$가 증가할 때 $y$도 증가하는 경향 (양의 상관 관계)
$\text{Cov}(x, y) < 0$	$x$가 증가할 때 $y$는 감소하는 경향 (음의 상관 관계)
$\text{Cov}(x, y) = 0$	$x$, $y$ 사이에 선형적인 관계 없음 (무상관)

 

공분산은 크기(scale)에 영향을 받기 때문에 절댓값만으로 두 변수의 관계가 얼마나 강한지는 판단할 수 없다. 

 

그래서 보통은 상관계수(correlation coefficient)를 같이 본다.

공분산과 공분산 행렬

 

다변량 정규 분포에서는 하나의 확률 변수가 아니라 벡터 형태의 확률 변수 $x = [x_1, x_2, ..., x_D]^T$를 사용한다. 

 

이 경우 공분산은 $D \times D$ 행렬로 확장된다.

 

• 이 행렬을 공분산 행렬(covariance matrix)이라고 부른다.
• 공분산 행렬의 성분은 다음과 같다:

$$Σ_{ij}=\text{Cov}(x_i,x_j)$$

 

 

즉,

 

• 대각 성분: $\Sigma_{ii} = \text{Var}(x_i)$ → 각 변수의 분산
• 비대각 성분: $\Sigma_{ij}$ → $x_i$와 $x_j$ 간의 공분산

공분산 행렬은 대칭 행렬이며, 항상 양의 정부호(positive definite) 또는 반정부호(semi-definite)이다.

 

예시로 보는 공분산

$x$	$y$	해석
키	몸무게	양의 공분산 → 키가 크면 몸무게도 증가
공부시간	시험점수	양의 공분산
커피 섭취량	수면 시간	음의 공분산 → 커피를 많이 마실수록 덜 잔다

 

정리

• 공분산은 두 변수 간의 선형적 관계를 정량화한 수치이다.
• 음수, 0, 양수로 해석되며, 방향은 알려주지만 강도는 상관계수를 통해 판단해야 한다.
• 공분산 행렬은 다변량 분포에서 중심성과 분산 구조를 전반적으로 나타내는 핵심 요소이다.
• 컴퓨터 비전이나 머신러닝에서는 Gaussian 분포, PCA, Kalman 필터, GMM 등 다양한 분야에서 필수적으로 등장한다.

3.9 켤레성 (Conjugacy) - 켤레로 관련된 그룹의 두 요소 간의 관계

 

앞서 살펴본 바와 같이, 베타 분포(beta distribution)는 

 

베르누이 분포(Bernoulli distribution)의 파라미터에 대한 확률을 표현할 수 있다. 

 

마찬가지로, 디리클레 분포(Dirichlet distribution)는 

 

범주형 분포(categorical distribution)의 파라미터에 대한 분포를 정의하며, 

 

정규-스케일드 역감마(normal-scaled inverse gamma)와 일변량 정규 분포(univariate normal), 

 

정규-역 위샤트(normal-inverse Wishart)와 다변량 정규 분포(multivariate normal) 사이에도 유사한 관계가 존재한다.

 

이러한 분포 쌍은 임의로 선택된 것이 아니라, 특별한 관계를 기반으로 구성된 것이다. 

 

구체적으로 말하면, 각각의 첫 번째 분포는 두 번째 분포에 대해 켤레(conjugate)이다. 

 

예를 들어, 베타 분포는 베르누이 분포에 대해 켤레이며, 디리클레는 범주형 분포에 대해 켤레이다.

켤레 관계란 다음과 같은 성질을 의미한다: 

 

어떤 분포와 그 분포에 대한 켤레 사전 분포(conjugate prior)를 곱했을 때, 결과가 켤레 분포와 같은 형태를 유지한다는 것이다. 

 

예를 들어 다음과 같은 관계가 성립한다:

 

$$\text{Bern}_x[λ]⋅\text{Beta}_λ[α,β]=κ(x,α,β)⋅\text{Beta}_λ[\widetilde{α},\widetilde{β}]\tag{3.17}$$

 

여기서 $\kappa(x, \alpha, \beta)$는 관심 변수 $\lambda$에 대해 상수인 정규화 계수(scaling factor)이다.

 

이 관계는 매우 중요한데, 이는 임의의 분포를 사전 분포로 사용했을 경우 

 

이러한 곱셈 결과가 동일한 형태를 유지하지 않을 수 있기 때문이다. 

 

켤레 쌍을 선택했기 때문에 위와 같은 정리된 형태를 얻을 수 있었던 것이다.

 

식 (3.19)의 관계는 다음과 같이 간단히 증명할 수 있다:

 

$$\begin{align*}\text{Bern}_x[λ]⋅\text{Beta}_λ[α,β] &= λ^x(1-λ)^{1-x}⋅\frac{\Gamma[\alpha+\beta]}{\Gamma[\alpha]\Gamma[\beta]}⋅λ^{\alpha-1}(1-λ)^{\beta-1} \\ &= \frac{\Gamma[\alpha+\beta]}{\Gamma[\alpha]\Gamma[\beta]}⋅λ^{x+\alpha-1}(1-λ)^{1-x+\beta-1} \\ &= \frac{Γ[α+β]}{Γ[α]Γ[β]}⋅\frac{Γ[x+α]Γ[1−x+β]}{Γ[x+α+1−x+β]}⋅\text{Beta}_λ[x+α,1−x+β] \\ &= κ(x,α,β)⋅\text{Beta}_λ[\widetilde{α},\widetilde{β}] \end{align*}\tag{3.20}$$

 

여기서 마지막 줄은 $x + \alpha = \widetilde{\alpha}$, $1 - x + \beta = \widetilde{\beta}$로 표기한 것이다. 

 

세 번째 줄에서는 $\text{Beta}_\lambda[\widetilde{\alpha}, \widetilde{\beta}]$에 해당하는 상수를 

 

분자와 분모에 동시에 곱하고 나누는 방식으로 정규화 계수를 도출하였다.

 

켤레 관계의 중요성

 

켤레성은 두 가지 주요 상황에서 결정적인 장점을 제공한다:

 

1. 학습 단계 (Learning) — 모델의 사후 분포를 계산할 때,
2. 추론 및 평가 단계 (Evaluation) — 학습된 분포에 대해 새로운 데이터의 가능도(likelihood)를 계산할 때,

위 두 과정에서 분포 간의 곱셈이 빈번하게 발생한다. 

 

이때 켤레 분포를 사용하면, 결과가 동일한 형태의 분포로 유지되기 때문에 

 

폐형(closed form)으로 정리할 수 있고, 계산적으로도 매우 효율적이다.

 

핵심 요약

• 켤레 분포는 결합 확률을 곱했을 때 같은 형태의 분포로 유지되는 사전 분포이다.
• 베타–베르누이, 디리클레–범주형, 정규-역감마–정규, 정규-역위샤트–다변량 정규가 대표적인 켤레 쌍이다.
• 켤레성을 활용하면 사후 분포 계산과 모델 평가를 정확하고 효율적으로 수행할 수 있다.
• 켤레 분포를 사용하지 않을 경우, 결과 분포가 복잡해져서 근사 또는 수치적 계산이 필요할 수 있다.

추가: 켤레 분포는 ‘형태를 보존’하는 사전 분포다

 

베이즈 추론에서 우리는 다음과 같은 사후 확률을 계산하게 된다:

 

$$Pr(y|x) = \frac{Pr(x|y)Pr(y)}{Pr(x)}$$

 

$$\text{Posterior}=\frac{\text{Likelihood} \times \text{Prior}}{\text{Evidence}}$$

 

즉, 관측 데이터에 대한 가능도(우도, likelihood)와 사전 분포(prior)를 곱한 후 정규화하면 사후 분포(posterior)가 된다.

 

그런데 중요한 점은 다음과 같다:

어떤 사전 분포(prior)를 선택하느냐에 따라,
사후 분포(posterior)의 형태가 완전히 바뀔 수도 있다.

 

하지만, 켤레 분포는 특별히 설계된 사전 분포라서,

사후 분포의 형태가 사전 분포와 동일하게 유지된다.

 

이게 켤레성(conjugacy)의 핵심이다. 예를 들어:

 

• 베르누이 분포의 파라미터 $\lambda$를 추론하려고 할 때,
• 사전 분포로 베타 분포를 사용하면,
• 데이터를 관측하고 likelihood를 곱한 후 계산한 사후 분포도 다시 베타 분포가 된다.

이처럼 켤레 분포는 마치 “곱셈을 해도 자기 자신이 돌아오는 구조”를 가지는데, 

 

여기서 선형대수학에서 고윳값(eigenvalue)과 닮은 점이 있다.

 

켤레성과 고윳값의 유사성

개념	의미	형식 보존
고윳값/고유벡터	선형 변환 $A$에 대해, $A v = \lambda v$를 만족하는 벡터 $v$	변환을 받아도 방향 유지
켤레 분포	likelihood를 곱해도 posterior가 prior와 같은 분포 형태	연산 후에도 분포의 형태 유지

이처럼, 고유벡터가 변환을 받아도 자기 자신의 “방향”을 유지하듯,

 

켤레 분포는 likelihood를 곱해도 자기 자신의 “분포 형태”를 유지한다.

즉, 켤레 분포는 베이즈 업데이트에 대해 닫혀 있는(closed under) 구조를 갖는다고 볼 수 있다.

 

켤레 분포에서의 $\kappa(x, \alpha, \beta)$: 정규화 상수 (Normalization Constant)

 

베이즈 추론에서는 다음과 같은 사후 분포를 계산한다:

 

$$\text{Posterior}∝\text{Likelihood}×\text{Prior}$$

 

그런데 우변은 대개 정규화되어 있지 않다. 

 

확률 분포로 만들기 위해서는 전체 면적(또는 합)이 1이 되도록 정규화해야 한다.

 

이때 곱 앞에 붙는 계수가 바로 $\kappa(x, \alpha, \beta)$이다.

 

즉:

 

• $\kappa$는 확률 변수 $\lambda$에 대해 상수이고,
• $\text{Posterior} = \kappa(x, \alpha, \beta) \cdot \text{Beta}(\tilde{\alpha}, \tilde{\beta})$ 처럼,
  결과 분포가 다시 베타 분포의 형태를 유지하도록 도와주는 정규화 계수다.
• 참고의 참고로, 따라서 $\kappa$는 evidence $Pr(x)$의 역수이다.

구분	선형변환의 $\lambda$	베이즈 추론의 $\kappa(x, \alpha, \beta)$
어떤 역할?	고유벡터의 스케일 변화율	정규화 상수 (확률 분포의 총합 = 1 유지)
무엇에 의존함?	행렬 $A$, 벡터 $\vec{v}$	관측값 $x$와 사전 분포의 파라미터 $\alpha, \beta$
어떤 대상에 대해 상수인가?	특정 고유벡터 $\vec{v}$에 대해 상수	관심 변수 $\lambda$에 대해 상수
목적	선형 변환의 축 방향 분석	베이즈 업데이트 결과를 분포로 정규화
핵심 기능	방향은 유지, 크기만 변형	분포 형태는 유지, 확률로 정규화

왜 켤레 분포가 중요한가?

 

켤레 분포의 장점은 다음과 같다:

 

1. 사후 분포를 해석하기 쉽다.
   사전 분포와 같은 분포이므로 결과를 이해하고 해석하기가 수월하다.
2. 수식이 정리되고 계산이 빠르다.
   적분 없이 폐형 해(closed-form solution)로 구할 수 있다.
   수치적 근사나 샘플링 없이도 깔끔하게 계산 가능.
3. 학습과 추론을 통일된 구조에서 처리 가능하다.

예시 다시 보기: 베르누이 + 베타

• 베르누이 분포: $x \sim \text{Bern}(\lambda)$
• 베타 분포: $\lambda \sim \text{Beta}(\alpha, \beta)$

이때 데이터를 관측한 후 업데이트된 사후 분포는:

 

$$λ∣x∼\text{Beta}(α+x,β+1−x)$$

 

즉, 여전히 Beta 분포 형태다. 단지 파라미터(파라미터)만 바뀐다.

 

정리: 켤레 분포는 “분포 공간의 고유 구조”

• 켤레 분포는 베이즈 추론에서 자기 동일성을 유지한다.
• 이는 고유벡터가 선형 변환 후에도 자기 방향을 유지하는 것과 유사하다.
• 켤레성은 수식의 단순화, 계산의 효율성, 그리고 모델링의 직관성에서 큰 장점을 제공한다.

---

 

요약

 

확률 분포는 세계의 상태(world state)와 이미지 데이터(image data)를 기술하기 위한 도구로 사용된다. 

 

본 장에서는 이러한 목적에 적합한 네 가지 분포를 소개하였다:

 

• 베르누이 분포(Bernoulli distribution)
• 범주형 분포(categorical distribution)
• 단변량 정규 분포(univariate normal distribution)
• 다변량 정규 분포(multivariate normal distribution)

또한, 위 네 가지 분포의 파라미터(parameter)에 대한 불확실성을 기술하기 위한 네 가지 분포도 함께 소개하였다:

 

 

• 베타 분포(beta distribution)
• 디리클레 분포(Dirichlet distribution)
• 정규-스케일드 역감마 분포(normal-scaled inverse gamma distribution)
• 정규-역위샤트 분포(normal-inverse Wishart distribution)

이들 분포는 짝(pair)을 이루며 특별한 관계를 갖는다. 

 

구체적으로, 두 번째 집합의 각 분포는 첫 번째 집합의 하나와 켤레 관계(conjugate relationship)를 가진다.

이러한 켤레 분포 관계는 관측된 데이터에 분포를 적합(fit)시키고, 

 

학습된 모델 하에서 새로운 데이터를 평가하는 과정을 수학적으로 단순화한다는 장점이 있다.