티스토리 뷰
확률 밀도 함수(Probability Density Function, pdf)
Vagabund.Gni 2025. 3. 25. 17:59목차
생각해 보면 대학원을 다닐 때도 pdf의 의미에 대해선 크게 관심이 없었다.
그냥 이런저런 성질을 가지고 있고 이렇게 쓴다.. 쓰면 되지 뭐.. 하고 썼는데
10년이나 넘게 지나 다시 마주친 건 운명이라는 생각이 들어서 베이즈 정리와 함께
제대로 공부하고 넘어가기로 했다.
10년 후의 나에게 도움이 되기를!
확률 밀도 함수(Probability Density Function, pdf)
확률 밀도 함수는 연속 확률 변수의 확률 분포를 수학적으로 표현하는 가장 핵심적인 도구이다.
확률 밀도 함수 Pr(x)는 확률 변수 x가 특정 값을 중심으로 얼마나 "밀집되어" 있는지를 나타내는 함수이다.
즉, x가 특정 값 근처에서 관측될 가능성의 상대적 크기를 나타낸다.
하지만 중요한 점은 다음과 같다:
확률 밀도 함수의 값 자체는 확률이 아니다.
예를 들어, Pr(x=1.5)=0.8이라고 해도 "x=1.5일 확률이 0.8이다"라는 뜻이 아니다.
연속 확률 변수의 경우, 정확히 하나의 값이 나올 확률은 항상 0이다.
연속 확률 변수의 경우, 정확히 하나의 값이 나올 확률은 항상 0이다.
이것은 또 무슨 말인가.
연속 확률 변수의 경우, 모든 값에 대해서 하나의 값이 나올 확률이 0이라니.
이 말은 직관적으로 이상하게 들릴 수 있지만, 확률론적으로는 정확히 맞는 말이다.
이 개념을 직관적으로, 그리고 수학적으로 살펴보자.
직관적 설명: 무한한 가능성 중 하나
연속 확률 변수는 실수(real number) 값을 갖는다. 예를 들어, 다음과 같은 경우를 생각해 보자:
- 어떤 사람이 시험을 치르는 데 걸리는 시간 x가 0시간 이상 2시간 이하일 때
온도 센서가 측정하는 값이 20.0000000도와 20.0000001도 사이의 어떤 실수 값일 때
이처럼 x는 실수 중에서 무한히 많은 값들 중 하나를 갖는다.
즉, x는 이론적으로 다음과 같은 무한히 많은 값 중에서 하나를 고르게 된다:
x=0.000...1,x=1.5,x=√2,x=π,...
이 무한한 후보 중 정확히 한 값을 택한다는 것은,
마치 0과 1 사이에서 바늘 하나를 던져서 "딱 0.5"에 꽂히기를 기대하는 것과 같다.
그렇게 "정확히 그 점"에 꽂힐 확률은 0이다.
수학적 설명
확률 밀도 함수(pdf) Pr(x)를 가진 연속 확률 변수 x에 대해, "x = a일 확률"은 다음과 같이 정의된다:
Pr(x=a)=∫aaPr(x)dx=0
어떤 구간 [a,b]에 대해 확률을 계산하려면:
Pr(a≤x≤b)=∫baPr(x)dx
여기서 구간의 양 끝이 같다면, 즉 a=b라면 적분 범위의 길이가 0이므로 결과는 항상 0이다.
오해 방지
그럼 확률이 0이니까 절대 발생할 수 없다는 말이냐? 절대 그렇지 않다.
연속 확률 변수의 경우, 확률이 0이라고 해서 발생 불가능한 것은 아니다.
“어떤 특정 값이 나올 확률이 0”일 수는 있어도, 실제로 그 값이 나오는 것은 가능하다.
다만, 그 값만 따로 집어 확률을 따지면, 전체 실수 집합 중 하나이기 때문에 0이 되는 것이다.
확률은 구간에 대해 정의된다
연속 확률 변수의 경우, 어떤 하나의 점에서의 확률은 의미가 없고, 어떤 구간에서 값이 나올 확률만이 의미가 있다.
예를 들어, 확률 변수 x가 구간 [a,b]에 속할 확률은 다음과 같이 계산된다:
Pr(a≤x≤b)=∫baPr(x)dx
여기서 Pr(x)는 확률 밀도 함수이며, 그 곡선 아래의 면적이 곧 확률이다.
확률 밀도 함수의 조건
모든 확률 밀도 함수는 다음의 두 조건을 만족해야 한다:
1. 비음수성
Pr(x)≥0for all x
어떤 값에서도 확률 밀도는 0 이상이어야 한다.
2. 정규화(normalization):
전체 실수 공간에 대해 적분한 값이 1이어야 한다. 즉, 어떤 값이든 어디에선가 나타날 확률이 100%라는 의미이다.
∫∞−∞Pr(x)dx=1
확률 밀도 함수 vs 이산 확률 분포
| 구분 | 이산 확률 변수 | 연속 확률 변수 |
| 확률 표현 | Pr(x=x∗) | Pr(a≤x≤b)=∫baPr(x)dx |
| 시각화 | 히스토그램, 힌튼 다이어그램 | 연속 곡선 (pdf) |
| 특정 값의 확률 | 0 이상 | 항상 0 |
| 합계 / 면적 | 확률의 합이 1 | 면적의 합이 1 |
예시: 정규 분포
가장 유명한 확률 밀도 함수 중 하나는 정규 분포(Normal Distribution)이다:
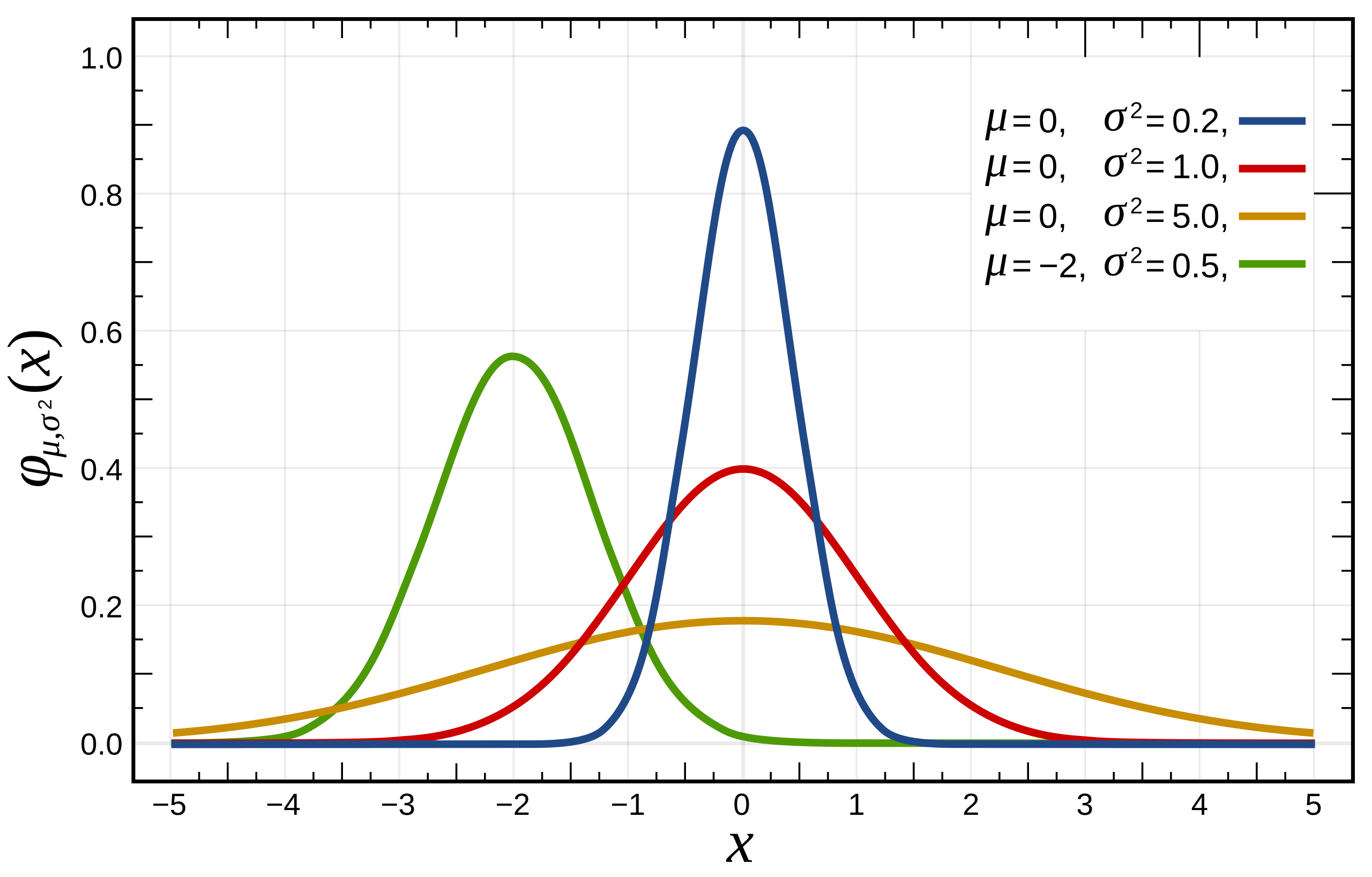
Pr(x)=1√2πσ2exp(−(x−μ)22σ2)
- μ는 평균 (mean)
- σ2는 분산 (variance)
정규 분포의 확률 밀도 함수는 종 모양을 띄며, 중심 μ에서 가장 높고, 멀어질수록 값이 줄어든다.
밀도가 1을 넘을 수도 있음
확률 밀도 함수는 값 자체가 확률이 아니므로 1을 초과할 수도 있다.
예를 들어, x가 매우 좁은 범위에서만 발생한다면, 그 구간의 pdf 값은 1보다 클 수 있다.
중요한 것은 전체 면적이 1이어야 한다는 것이다.
예시: 확률 밀도 함수의 값이 1보다 큰 경우
이건 또 뭔 소린가. 침착하게 확률 변수 x가 구간 [0,0.1]에서 균등하게 분포한다고 하자.
이때 확률 밀도 함수는 다음과 같다:
Pr(x)=10.1=10for 0≤x≤0.1
즉, 확률 밀도 함수의 값이 10, 즉 1보다 훨씬 크다.
왜 10이어도 괜찮을까?
확률 분포에서 중요한 것은 “곡선 아래 면적의 합이 1이어야 한다는 것”이다.
이 예에서는 구간 너비가 0.1이고, 높이가 10이므로 면적은:
면적=너비×높이=0.1×10=1
따라서 확률 분포의 조건을 완벽히 만족한다.
정리
- 확률 밀도 함수의 값(pdf 값)은 확률이 아니라 상대적인 밀도이다.
- 따라서 1을 초과할 수 있다.
- 전체 곡선 아래 면적이 1이 되기만 하면 pdf 값이 얼마든 커도 괜찮다.
- 구간이 좁을수록(예: [0, 0.0001]) pdf 값은 더 커질 수 있다.
요약
- 확률 밀도 함수는 연속 확률 변수의 확률 분포를 나타냄.
- 특정한 점에서의 확률은 항상 0.
- 구간에 대한 확률은 밀도 함수의 적분값으로 계산.
- 밀도 함수는 0 이상이며 전체 면적은 1이어야 함.
- 값 자체가 확률은 아니며 1을 초과할 수 있음.
'ML+DL > Computer Vision By Simon J.D. Prince' 카테고리의 다른 글
| Chapter 3: Common Probability Distributions (0) | 2025.04.03 |
|---|---|
| 감마 함수 (Gamma Function) (1) | 2025.03.26 |
| 확률 모델의 불확실성? 베이지안 관점에서의 하이퍼파라미터 (0) | 2025.03.25 |
| Chapter 2: Introduction to probability (0) | 2025.03.21 |
| 베이즈 정리(Bayes' theorem) (0) | 2025.03.21 |
| Part I: Probability (0) | 2025.03.19 |
- Total
- Today
- Yesterday
- 유럽여행
- Backjoon
- 여행
- 세계여행
- 백준
- java
- 야경
- 세모
- 알고리즘
- 중남미
- 기술면접
- a6000
- BOJ
- 칼이사
- 지지
- 스트림
- Algorithm
- RX100M5
- 유럽
- 맛집
- 남미
- Python
- 스프링
- 세계일주
- 리스트
- spring
- 자바
- 파이썬
- 동적계획법
- 면접 준비
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
