딥러닝에서의 최적화: 하강법과 경사하강법

목차

 

딥러닝의 역사와 발전: 머신러닝에서 딥러닝까지의 여정

인공 신경망의 기본 구조와 중요성

활성화 함수(Activation Functions) 이해하기

손실 함수(Loss Functions)의 역할과 중요성

딥러닝에서의 최적화: 하강법과 경사하강법

확률적 경사 하강법(Stochastic Gradient Descent, SGD)

기울기 사라짐(Vanishing Gradient)

손실 함수와 최적화

컴퓨터 비전(Computer Vision)

합성곱 연산(Convolution)

합성곱 신경망(Convolutional Neural Network, CNN)

순환 신경망(Recurrent Neural Network, RNN)

순환 신경망의 발전(The Evolution of RNN)

오토 인코더(Autoencoder)

생성적 적대 신경망(Generative Adversarial Network, GAN)

과적합과 그 방지법

데이터 불균형

딥러닝 모델 튜닝: 성능 향상의 기초와 전략

전이 학습(Transfer Learning)

딥러닝 학습 방법: 지도학습부터 강화학습까지

설명 가능한 AI(Explainable AI, XAI)

Introduction

 

딥러닝과 머신러닝에서 최적화는 모델의 성능을 극대화하고, 예측 오차를 최소화하는 과정이다. 

 

이 게시글에서는 최적화의 핵심 요소인 목적 함수, 하강법, 특히 경사 하강법에 대해 자세히 알아본다.

 

Optimization

 

최적화(Optimization)란 복잡한 문제를 해결하는 과정에서,

 

특정 수학적 함수의 값을 최소화하거나 최대화하여 최적의 결과를 찾아가는 과정을 말한다.

 

특히 딥러닝 분야에서는 모델이 학습하는 과정 중에 손실 함수라 불리는 특정 함수의 값을 최소화함으로써,

 

모델의 예측치가 실제 데이터의 값에 가능한 가깝게 되도록 조정하는 작업을 말한다.

 

이 과정에서 모델 내부의 가중치(Weights)들을 조절하며, 이를 통해 모델의 성능을 점차적으로 향상하고,

 

최적의 예측 결과를 얻기 위한 가중치의 조합을 찾아가는 것이 핵심 목표가 된다.

 

이러한 최적화 과정은 모델이 데이터로부터 학습하고,

 

실제 세계의 복잡한 문제들을 보다 정확하게 예측할 수 있게 하는 데 있어 필수적인 단계이다.

 

Objective Function

 

목적 함수는 최적화 과정에서 최소화하려는 대상이다. 

 

예를 들어, 손실 함수는 실제 값과 모델의 예측 값 사이의 차이를 수치화한 것으로, 이 값을 최소화하는 것이 목표다. 

 

목적 함수를 통해 모델의 성능을 평가하고, 이를 최적화함으로써 더 나은 예측 결과를 얻을 수 있다.

 

Descent Method

 

하강법(Descent Method)은 수학과 컴퓨터 과학에서 널리 사용되는 최적화 기법으로, 

 

특정 목적 함수의 최솟값을 찾는 데 목적을 둔다. 

 

기본 아이디어는 목적 함수의 현재 위치에서 기울기(Gradient)를 계산하고, 

 

이 기울기가 가리키는 방향의 반대로 이동하는 것이다. 

 

이 과정을 반복함으로써, 함수의 최솟값에 점차 가까워진다. 

 

하강법의 핵심 요소는 다음의 두 가지, 탐색방향(Search Direction)과 학습률(Learning Rate, Step Size)로 구성된다.

 

• 탐색 방향은 기울기의 반대 방향으로, 함수의 값을 줄이는 방향을 의미한다.
• 학습률은 이동할 크기를 결정하며, 너무 크면 최솟값을 지나치고, 너무 작으면 최적화 속도가 느려질 수 있다.

따라서, 하강법을 사용할 때는 이 두 요소를 신중하게 조절하여 최적의 결과를 얻어야 한다.

 

Gradient Descent

 

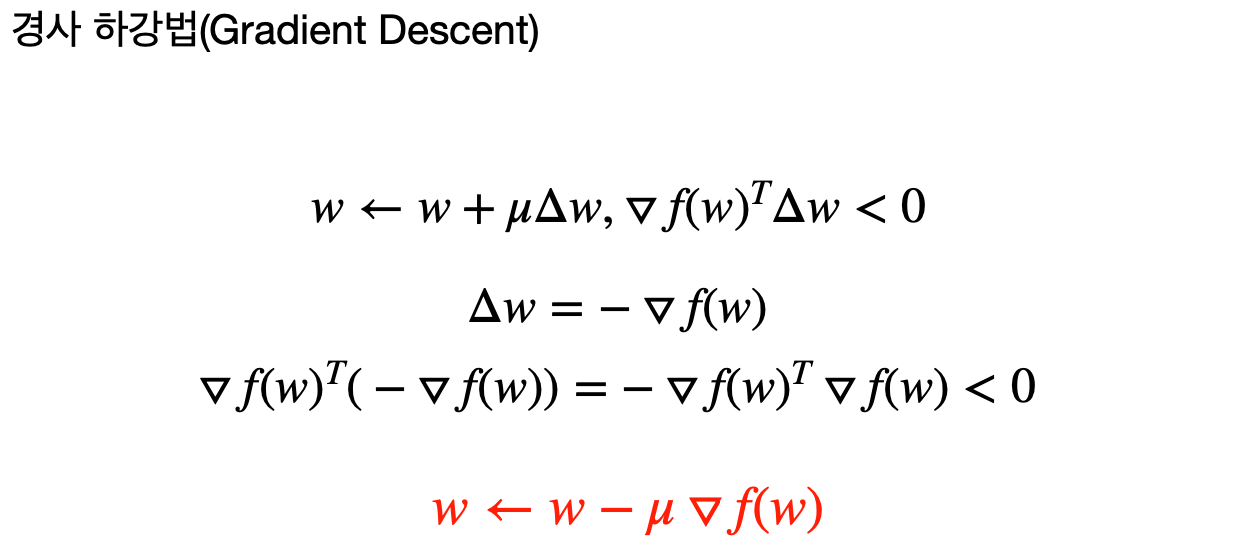
경사 하강법은 하강법의 가장 널리 사용되는 형태로, 

 

각 단계에서 함수의 기울기(또는 그래디언트)를 사용해 다음 위치를 결정한다. 

 

이 방법은 간단하면서도 효과적이어서 다양한 최적화 문제에 사용된다.

 

Backpropagation

 

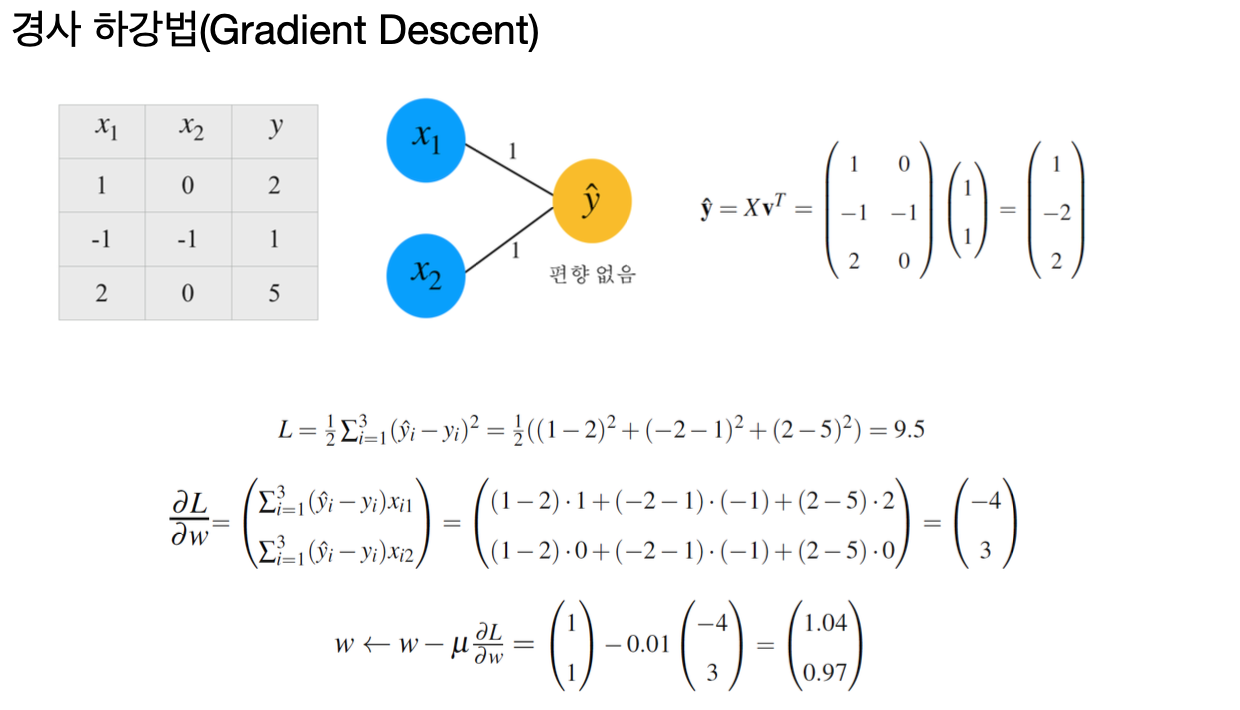
경사 하강법을 효율적으로 수행하기 위해선, 목적함수의 기울기를 정확하게 계산해야 한다. 

 

이를 위해 사용되는 기술이 바로 역전파다. 

 

역전파는 출력층에서 입력층으로 거슬러 올라가며 각 뉴런의 출력에 대한 오차의 기울기를 계산하고, 

 

이를 통해 파라미터를 조정한다. 

 

이 과정은 네트워크의 파라미터가 목적함수의 최솟값을 향해 효과적으로 조정될 수 있게 해 준다.

 

 

Conclusion

 

경사 하강법과 하강법의 이해는 딥러닝과 머신러닝 모델을 최적화하는 데 있어 핵심적인 요소다. 

 

이러한 최적화 기법들을 통해 모델의 성능을 향상하고, 예측의 정확도를 높일 수 있다. 

 

특히, 목적 함수의 최솟값을 찾는 과정에서는 탐색 방향과 학습률의 조절이 중요하며, 

 

이는 모델 학습의 효율성과 최종 성능에 큰 영향을 미친다.

따라서, 딥러닝 모델을 훈련시킬 때, 적절한 학습률을 설정하고, 목적 함수의 변화를 주의 깊게 관찰하는 것이 필수적이다. 

 

이를 통해, 모델이 더 빠르고 효율적으로 최적의 가중치에 도달하도록 할 수 있다.