손실 함수와 최적화

목차

 

딥러닝의 역사와 발전: 머신러닝에서 딥러닝까지의 여정

인공 신경망의 기본 구조와 중요성

활성화 함수(Activation Functions) 이해하기

손실 함수(Loss Functions)의 역할과 중요성

딥러닝에서의 최적화: 하강법과 경사하강법

확률적 경사 하강법(Stochastic Gradient Descent, SGD)

기울기 사라짐(Vanishing Gradient)

손실 함수와 최적화

컴퓨터 비전(Computer Vision)

합성곱 연산(Convolution)

합성곱 신경망(Convolutional Neural Network, CNN)

순환 신경망(Recurrent Neural Network, RNN)

순환 신경망의 발전(The Evolution of RNN)

오토 인코더(Autoencoder)

생성적 적대 신경망(Generative Adversarial Network, GAN)

과적합과 그 방지법

데이터 불균형

딥러닝 모델 튜닝: 성능 향상의 기초와 전략

전이 학습(Transfer Learning)

딥러닝 학습 방법: 지도학습부터 강화학습까지

설명 가능한 AI(Explainable AI, XAI)

Limitations of Descent Method

 

하강법은 손실 함수의 기울기를 사용하여 최솟값을 찾는 방법이다. 

 

이 방법은 최적화 문제에서 중요한 역할을 하지만, 복잡한 모델과 데이터에서는 한계를 갖는다. 

 

그 이유 중 하나는 지역 최솟값(local minimum) 또는 안장점(saddle points)에 빠질 수 있다는 점이다.

 

이는 함수의 기울기가 0이 되는 지점이 반드시 전체 최솟값이 아닐 수 있기 때문이다.

 

특히, 비볼록(non-convex) 함수에서는 여러 지역 최솟값이 존재할 수 있으며,

 

이는 하강법이 전역 최솟값(global minimum)에 도달한다는 보장을 하지 못한다.

 

Loss Functions

 

손실 함수는 모델의 예측값과 실제 값 사이의 차이를 수치화한다. 

 

평균 절대 오차(MAE), 평균 제곱 오차(MSE), 크로스 엔트로피(Cross Entropy)는 대표적인 손실 함수이며 

 

볼록성(Convexity)을 지닌다. 

 

볼록 함수는 어떤 직선을 그렸을 때, 그 직선이 함수의 그래프와 접하거나 그 위에 있을 경우를 말한다. 

 

볼록성을 갖는 손실 함수를 사용하면 하강법과 같은 최적화 알고리즘이 지역 최솟값에 갇히지 않고 

 

전역 최솟값을 찾을 가능성이 높아진다.

 

Relationship between Convexity and Optimization

 

 

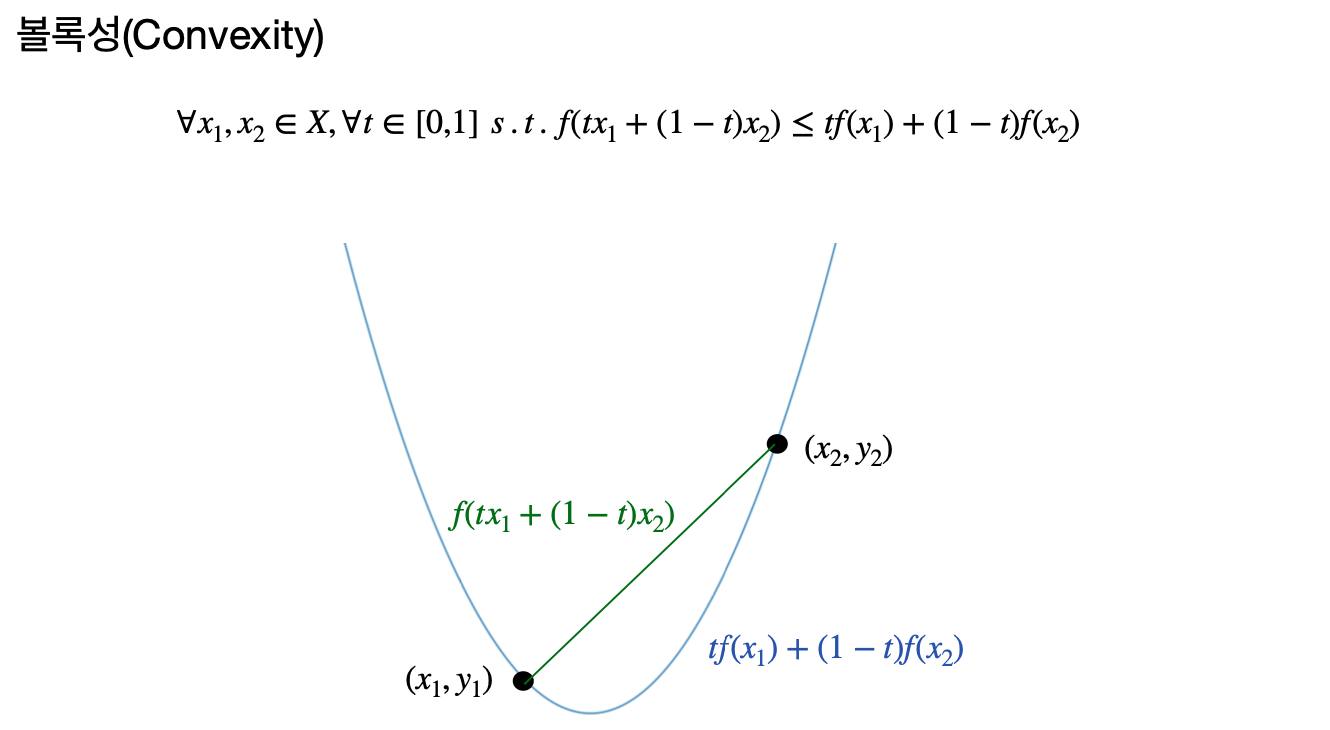
이는 볼록 함수의 어떤 두 점을 선택했을 때, 그 점들을 잇는 선분이 함수의 그래프 위에 있음을 의미한다. 

 

이 성질은 볼록 최적화 문제에서 하강법을 사용할 때, 매 반복마다 전역 최솟값에 점점 더 가까워진다는 것을 보장한다. 

 

따라서 볼록 함수의 최적화는 매우 중요하며, 

 

이는 머신러닝 모델을 훈련시킬 때 안정적이고 예측 가능한 결과를 얻을 수 있게 한다.

 

Convexity

 

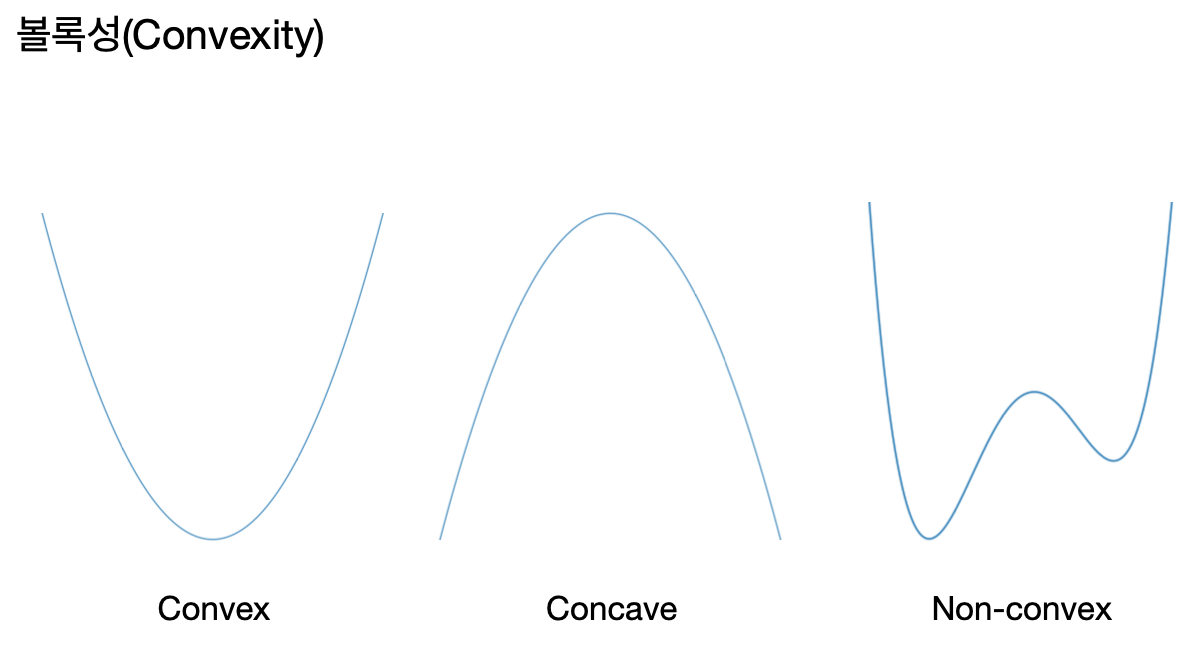
볼록성은 함수가 지닌 중요한 기하학적 특성이다. 

 

함수가 오목(concave) 일 때 그 음수는 볼록(convex)이 되며, 

 

이는 최적화 과정에서 목적 함수를 변형하는 데 사용될 수 있다. 

 

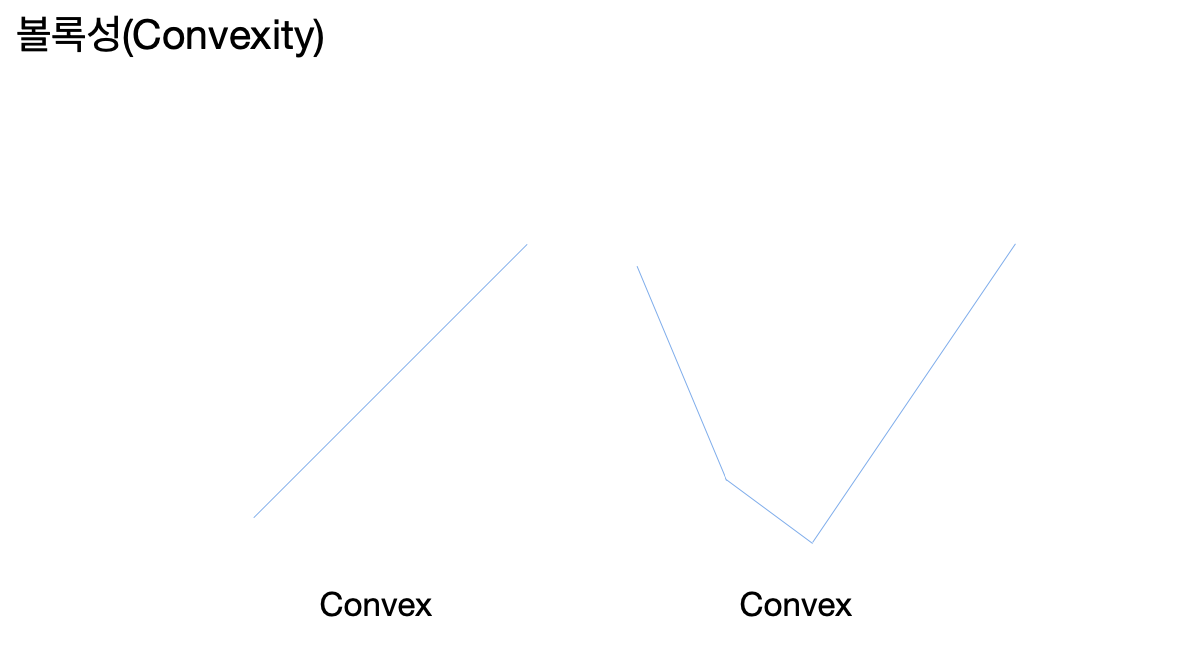
두 볼록 함수의 선형 조합이나 최댓값 또한 볼록함을 유지한다. 

 

모든 놈(norm)이 볼록하다는 것도 최적화에 유용한 속성이다. 

 

두 함수가 볼록하고, 한 함수가 다른 함수의 일변수 증가함수일 경우, 이들의 합성함수도 볼록함을 보인다.