활성화 함수(Activation Functions) 이해하기

목차

 

딥러닝의 역사와 발전: 머신러닝에서 딥러닝까지의 여정

인공 신경망의 기본 구조와 중요성

활성화 함수(Activation Functions) 이해하기

손실 함수(Loss Functions)의 역할과 중요성

딥러닝에서의 최적화: 하강법과 경사하강법

확률적 경사 하강법(Stochastic Gradient Descent, SGD)

기울기 사라짐(Vanishing Gradient)

손실 함수와 최적화

컴퓨터 비전(Computer Vision)

합성곱 연산(Convolution)

합성곱 신경망(Convolutional Neural Network, CNN)

순환 신경망(Recurrent Neural Network, RNN)

순환 신경망의 발전(The Evolution of RNN)

오토 인코더(Autoencoder)

생성적 적대 신경망(Generative Adversarial Network, GAN)

과적합과 그 방지법

데이터 불균형

딥러닝 모델 튜닝: 성능 향상의 기초와 전략

전이 학습(Transfer Learning)

딥러닝 학습 방법: 지도학습부터 강화학습까지

설명 가능한 AI(Explainable AI, XAI)

Introduction

 

딥러닝과 머신러닝의 세계에 발을 들이면, 

 

가장 먼저 마주치게 되는 용어 중 하나가 바로 '활성화 함수(Activation Function)'이다. 

 

여기서는 매우 간단한 개념으로 시작해서, 왜 이런 함수가 필요한지, 어떤 종류의 함수들이 존재하는지에 대해 알아보자.

 

Activation Function

 

활성화 함수는 인공 신경망에서 입력 신호의 총합을 출력 신호로 변환하는 함수다. 

 

즉, 신경망의 뉴런에 들어오는 입력값에 대해, 

 

어떤 특정한 처리를 거친 후 다음 뉴런으로 전달할 출력값을 결정하는 역할을 한다. 

 

활성화 함수 없이는 신경망이 복잡한 문제를 풀기 어렵다. 

 

왜냐하면 활성화 함수가 비선형성을 도입하기 때문이다. 

 

비선형 함수를 사용함으로써 신경망은 더 복잡한 패턴과 데이터를 학습할 수 있게 된다.

 

Necessity

 

신경망에서 활성화 함수가 없다면, 무슨 일이 벌어질까? 

 

신경망의 각 레이어는 단순히 선형 변환(즉, 가중치에 의한 입력값의 합)을 수행하게 된다. 

 

이러한 선형 변환들이 아무리 많이 쌓여 있다 하더라도, 전체 네트워크는 여전히 선형 함수 하나와 다를 바 없게 된다. 

 

즉, 신경망이 복잡한 패턴을 모델링하거나 학습할 수 있는 능력이 매우 제한적이 될 것이다.

활성화 함수를 사용함으로써, 신경망은 비선형성을 획득하게 되고, 

 

이는 신경망이 더 복잡하고 다양한 데이터의 패턴을 학습할 수 있게 해 준다. 

 

예를 들어, 이미지 인식, 자연어 처리, 게임 플레이어 등 고도로 복잡한 문제들을 해결하는 데 필수적이다.

 

Types of Activation Functions

 

다양한 활성화 함수들이 있는데, 각각의 함수는 특정 목적과 상황에 맞게 설계되었다. 여기 몇 가지 주요 활성화 함수를 소개한다:

 

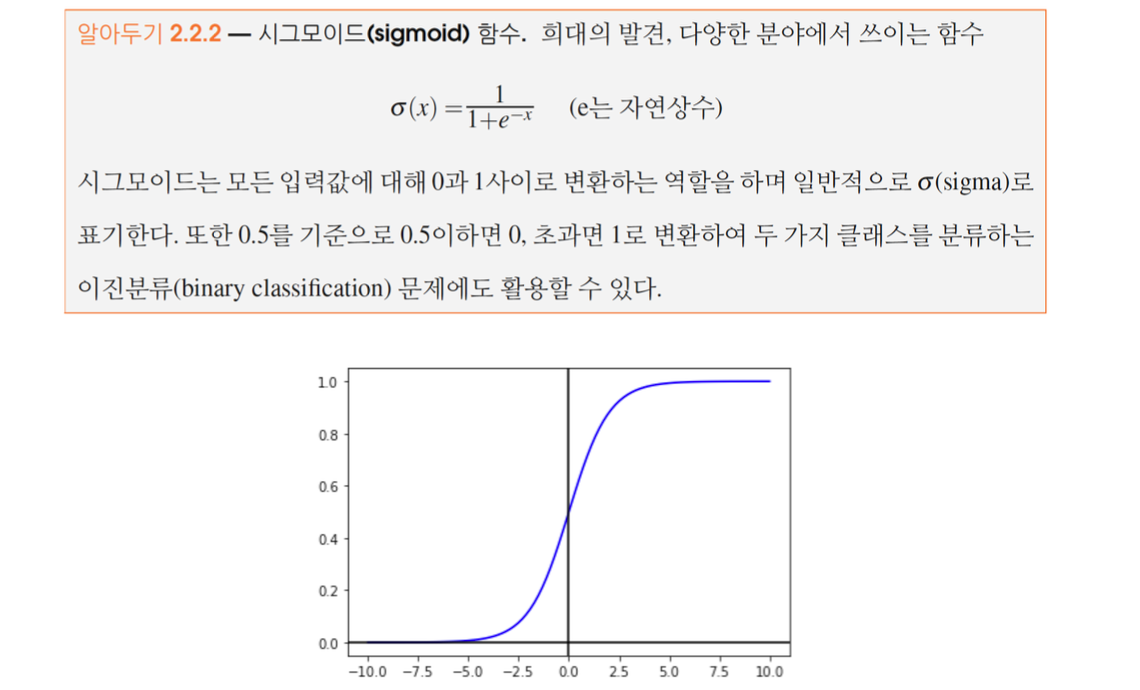
• 시그모이드(Sigmoid)

시그모이드 함수는 $a(x) = \frac{1}{1 + e^{-x}}$ 형태로, 출력값을 0과 1 사이로 압축한다. 이는 확률을 나타낼 때 유용하다.

 

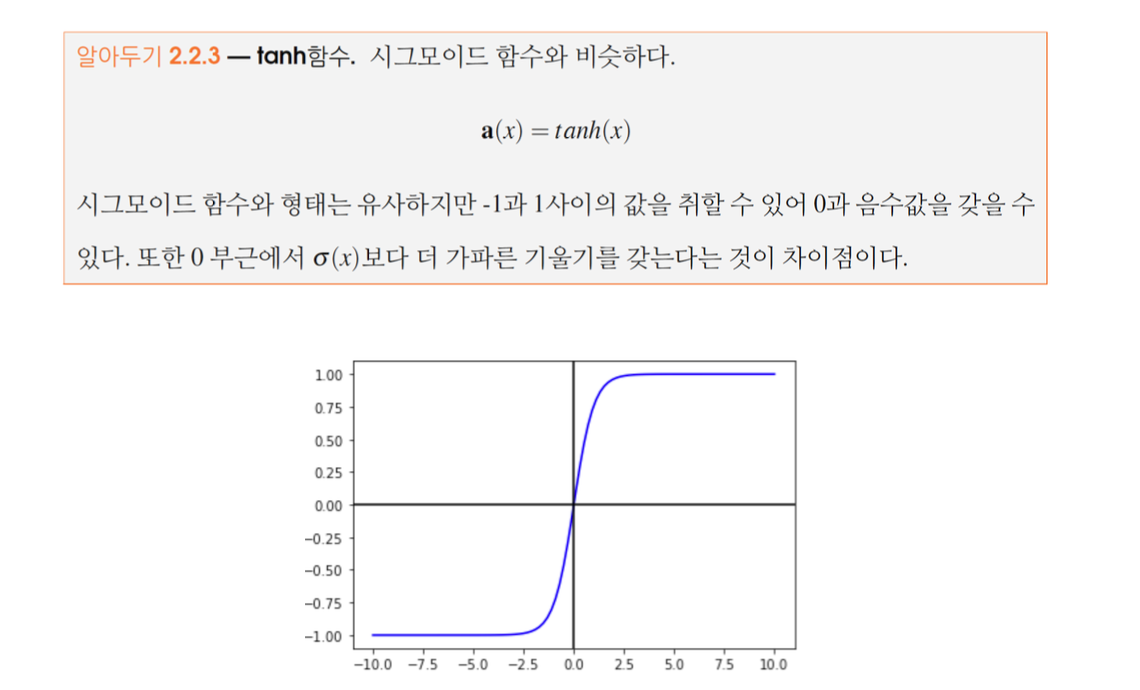
• 하이퍼볼릭 탄젠트(Hyperbolic Tangent, tanh)

$tanh$ 함수는 시그모이드와 유사하지만, 출력 범위가 -1에서 1 사이다.

 

이는 데이터의 중심이 0으로 이동하게 해주어 학습을 더 쉽게 만든다.

 

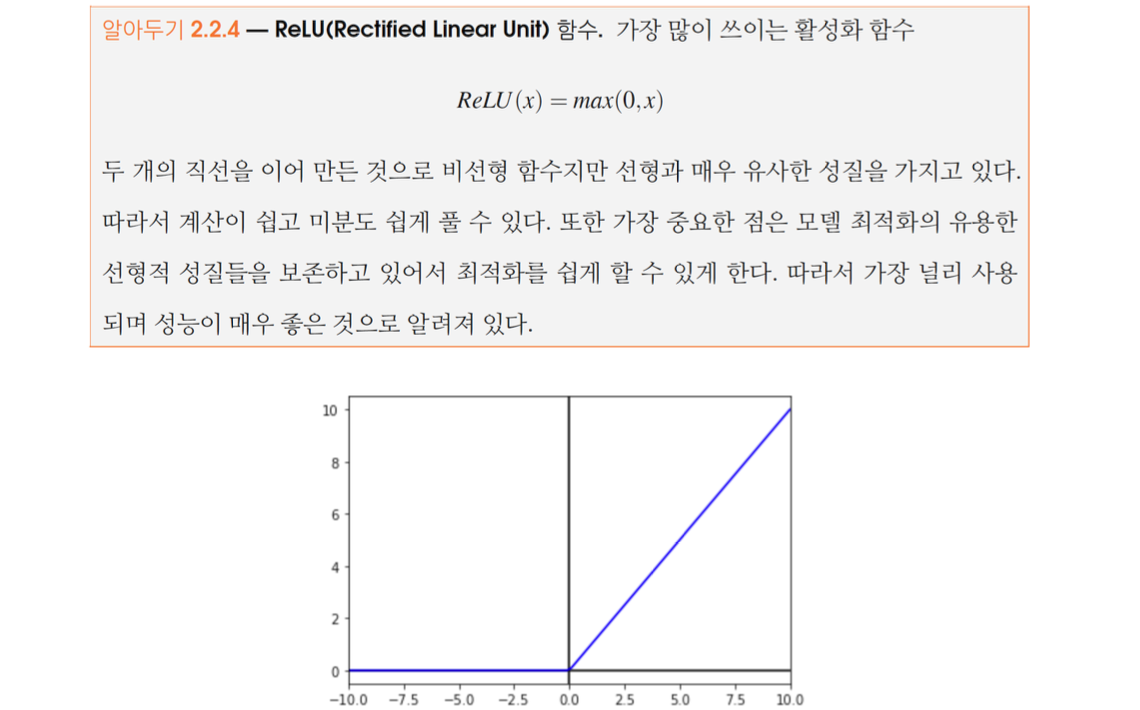
• ReLU(Rectified Linear Unit)

ReLU는 $a(x)=max(0,x)$로 정의되며, 현재 가장 인기 있는 활성화 함수 중 하나다.

 

계산이 효율적이면서도, 과적합을 방지하고 연산 비용을 낮춰주는 이점이 있다.

 

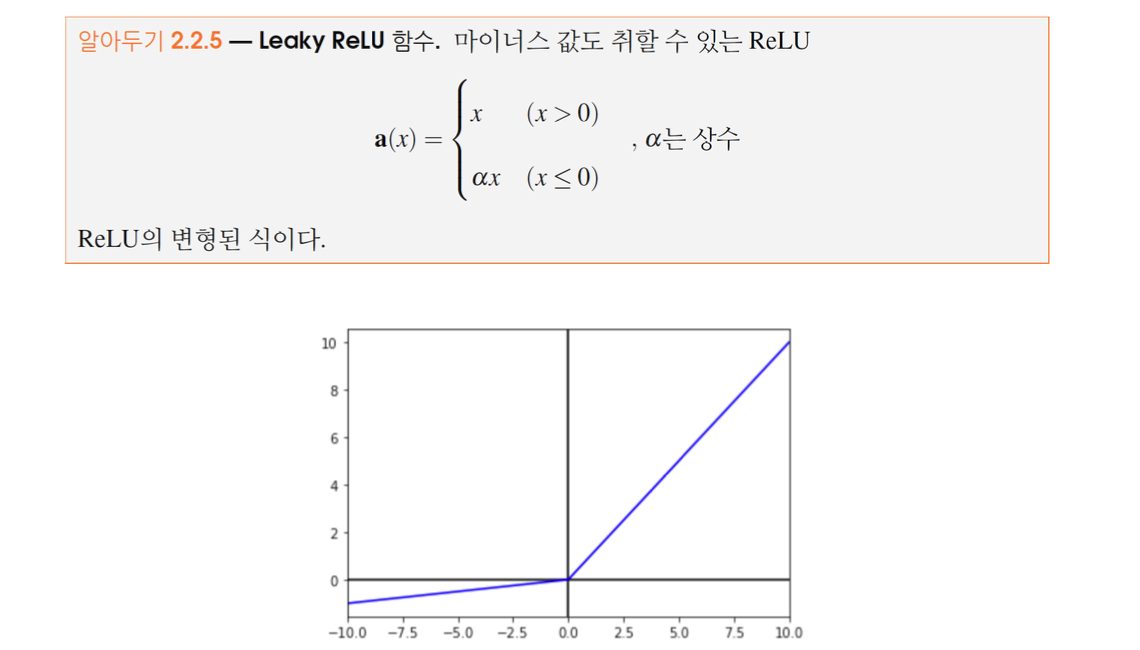
• Leaky ReLU

Leaky ReLU는 ReLU의 변형으로, 음수 입력값에 대해 아주 작은 기울기를 부여함으로써 '죽은 뉴런' 문제를 해결한다.

 

• Swish

Swish 함수는 $f(x) = x * sigmoid(x)$로 정의되며, 특정 조건에서 ReLU보다 성능이 좋다는 연구 결과가 있다.

 

• SELU(Self-Normalizing Neural Networks)

SELU는 자체 정규화 기능을 가진 활성화 함수로, 특정 조건에서 네트워크의 각 층에서의 출력이 평균 0, 분산 1을 유지하도록 설계되었다.

 

Conclusion

 

활성화 함수는 신경망의 핵심 요소 중 하나로, 신경망이 복잡한 문제를 해결할 수 있는 능력을 부여한다. 

 

다양한 활성화 함수가 존재하며, 각각의 함수는 특정 상황에서 최적의 성능을 발휘하도록 설계되었다. 

 

따라서 프로젝트의 요구사항과 데이터의 특성에 맞춰 적절한 활성화 함수를 선택하는 것이 중요하다. 

 

활성화 함수의 선택은 신경망의 성능에 직접적인 영향을 미치므로, 

 

다양한 함수를 실험해 보고 최적의 결과를 얻는 것이 바람직하다.