[선형대수학]벡터 공간과 기저, 차원 그리고 ML/DL

목차

 

[선형대수학]머신러닝과 딥 러닝의 핵심, 선형대수학의 역할과 중요성

[선형대수학]부분행렬과 분할행렬: 공통점과 차이점, ML/DL에의 응용

[선형대수학]역행렬과 행렬식의 성질, ML/DL과의 관계

[선형대수학]행렬의 해와 감소된 행 계단형(Reduced Row Echelon Form, RREF)

[선형대수학]벡터 공간(Vector Spaces)

[선형대수학]벡터 공간과 일차 독립

[선형대수학]벡터 공간과 기저, 차원 그리고 ML/DL

[선형대수학]차원의 저주: 데이터 분석의 걸림돌

[선형대수학]행렬의 랭크와 그 응용

[선형대수학]벡터의 내적과 그 응용

[선형대수학]정규직교 기저와 그람-슈미트 프로세스

[선형대수학]최소 제곱해

[선형대수학]선형변환과 고윳값의 이해: 머신러닝/딥러닝에서의 응용

[선형대수학]벡터 공간의 대각화와 그 응용 - 유사 행렬 및 머신러닝에서의 중요성

[선형대수학]특이값 분해(SVD): 기본부터 머신러닝/딥러닝까지의 응용

[선형대수학]특이값 분해와 고윳값: 공통점과 차이점

[선형대수학]실 이차 형식과 양의 정부호 행렬: 머신러닝/딥러닝에의 응용

[선형대수학]주성분 분석(Principal Component Analysis, PCA)

[선형대수학]Factorization Machines

 

Introduction

 

벡터 공간은 수학과 과학 전반에 걸쳐 기본적인 구조를 제공한다. 

 

특히, 기저는 벡터 공간을 구성하는 도구로서, 모든 벡터가 기저 벡터들의 유일한 선형 조합으로 표현될 수 있다. 

 

차원은 기저의 크기로 정의되며, 이는 공간의 '넓이'를 측정한다. 

 

이러한 개념들은 머신러닝과 딥러닝에서 데이터를 표현하고 처리하는 데 중심적인 역할을 한다.

 

Basis

 

기저는 벡터 공간을 이루는 일련의 벡터들로서, 이 벡터들이 선형 독립이며 공간을 Span 한다. 

 

즉, 공간 내의 모든 벡터는 기저 벡터들의 선형 조합으로 표현될 수 있다. 

 

예를 들어, $ \mathbb{R}^2$공간에서 (1,0)과 (0,1)은 표준 기저를 형성한다. 

 

기저는 고유하게 정의되지 않으며, 다양한 기저가 존재할 수 있다.

 

 

Dimension

 

차원은 기저 벡터의 수를 나타낸다. 이는 벡터 공간의 '크기'를 측정하는 방법으로,

 

공간 내에서 서로 독립인 최대 벡터의 수를 의미한다.

 

예를 들어, $ \mathbb{R}^3$의 차원은 3이며,

 

이는 공간을 Span하는 세 개의 선형 독립 벡터가 존재함을 나타낸다.

 

 

ML/DL

 

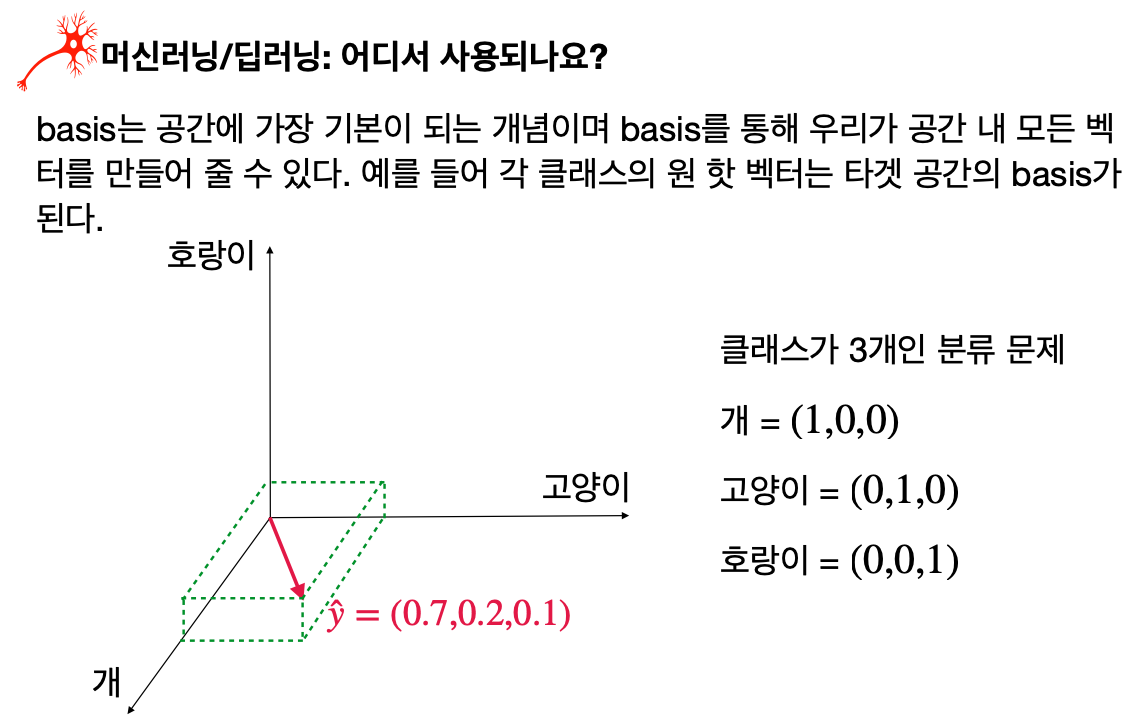
머신러닝과 딥러닝에서 기저와 차원은 데이터를 표현하는 데 필수적이다. 

 

차원의 저주를 피하기 위해 차원 축소 기법이 사용되며, 

 

이는 데이터의 복잡성을 줄이고 학습을 효율적으로 만든다. 

 

고차원 데이터를 처리할 때 기저와 차원의 선택은 알고리즘의 효율성과 성능에 큰 영향을 미친다.