[선형대수학]벡터 공간(Vector Spaces)

목차

 

[선형대수학]머신러닝과 딥 러닝의 핵심, 선형대수학의 역할과 중요성

[선형대수학]부분행렬과 분할행렬: 공통점과 차이점, ML/DL에의 응용

[선형대수학]역행렬과 행렬식의 성질, ML/DL과의 관계

[선형대수학]행렬의 해와 감소된 행 계단형(Reduced Row Echelon Form, RREF)

[선형대수학]벡터 공간(Vector Spaces)

[선형대수학]벡터 공간과 일차 독립

[선형대수학]벡터 공간과 기저, 차원 그리고 ML/DL

[선형대수학]차원의 저주: 데이터 분석의 걸림돌

[선형대수학]행렬의 랭크와 그 응용

[선형대수학]벡터의 내적과 그 응용

[선형대수학]정규직교 기저와 그람-슈미트 프로세스

[선형대수학]최소 제곱해

[선형대수학]선형변환과 고윳값의 이해: 머신러닝/딥러닝에서의 응용

[선형대수학]벡터 공간의 대각화와 그 응용 - 유사 행렬 및 머신러닝에서의 중요성

[선형대수학]특이값 분해(SVD): 기본부터 머신러닝/딥러닝까지의 응용

[선형대수학]특이값 분해와 고윳값: 공통점과 차이점

[선형대수학]실 이차 형식과 양의 정부호 행렬: 머신러닝/딥러닝에의 응용

[선형대수학]주성분 분석(Principal Component Analysis, PCA)

[선형대수학]Factorization Machines

 

Introduction

 

벡터 공간은 선형대수학의 핵심적인 구조로, 각종 수학적 문제를 기하학적인 관점에서 접근할 수 있는 기반을 제공한다.

 

또한 복잡한 현실 세계 문제를 모델링하고 해결하는 기본 도구로 사용되는데, 

 

이 글에서는 벡터 공간의 정의와 성질, 정의와 연산, 그리고 ML/DL에서 벡터 공간이 갖는 의미에 대해 정리한다.

 

Vector

 

벡터는 크기와 방향을 가진 양으로, 물리학에서는 힘과 속도 등을 표현하는 데 사용된다. 

 

수학에서는 숫자의 순서쌍이나 1xn 행렬 등으로 표현되며, 벡터 간의 연산을 통해 공간을 구성하는 기본 단위로 사용된다.

 

추가로, 크기와 방향이 같다면 같은 벡터로 간주한다.

 

Vector Operations

 

벡터 연산에는 기본적으로 벡터의 덧셈과 뺄셈, 그리고 스칼라 배가 포함된다.

 

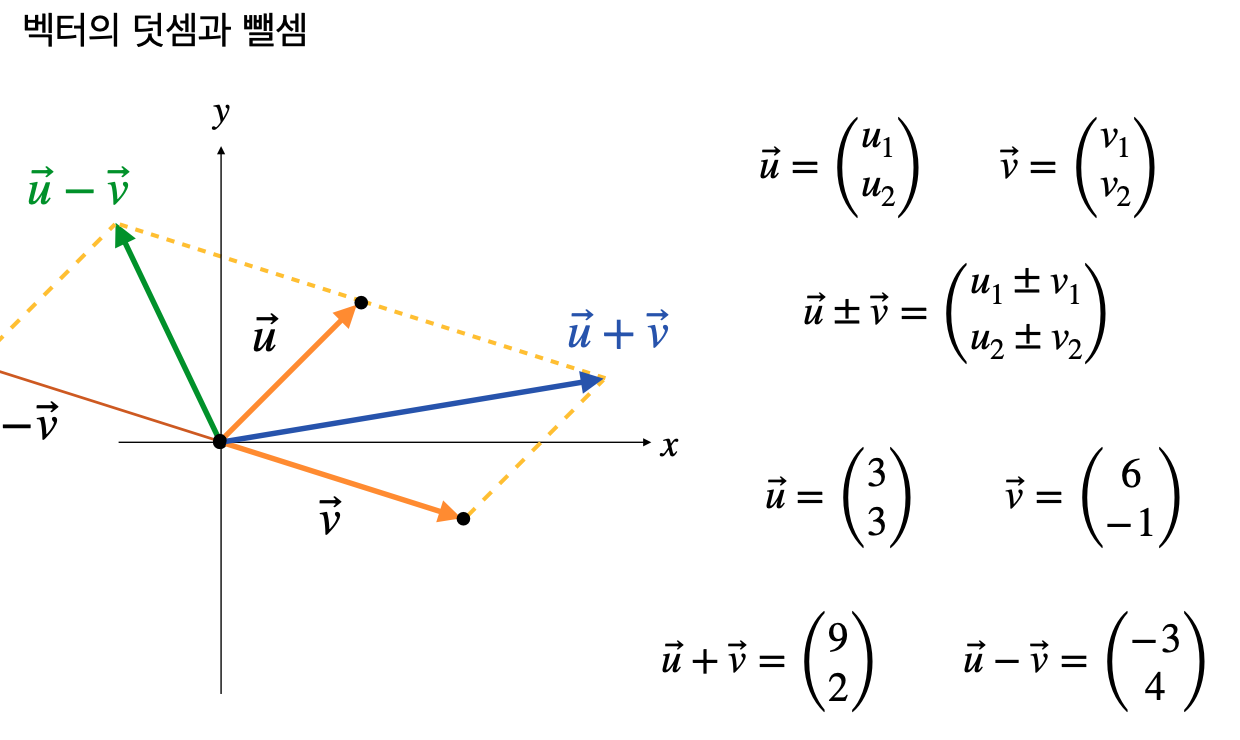
벡터 덧셈은 두 벡터의 각 성분을 더하는 것으로, 기하학적으로는 벡터를 평행이동시켜 나란히 놓고 결과 벡터를 도출한다. 

 

벡터 뺄셈은 덧셈의 반대로, 벡터의 방향을 반대로 하여 더한다. 

 

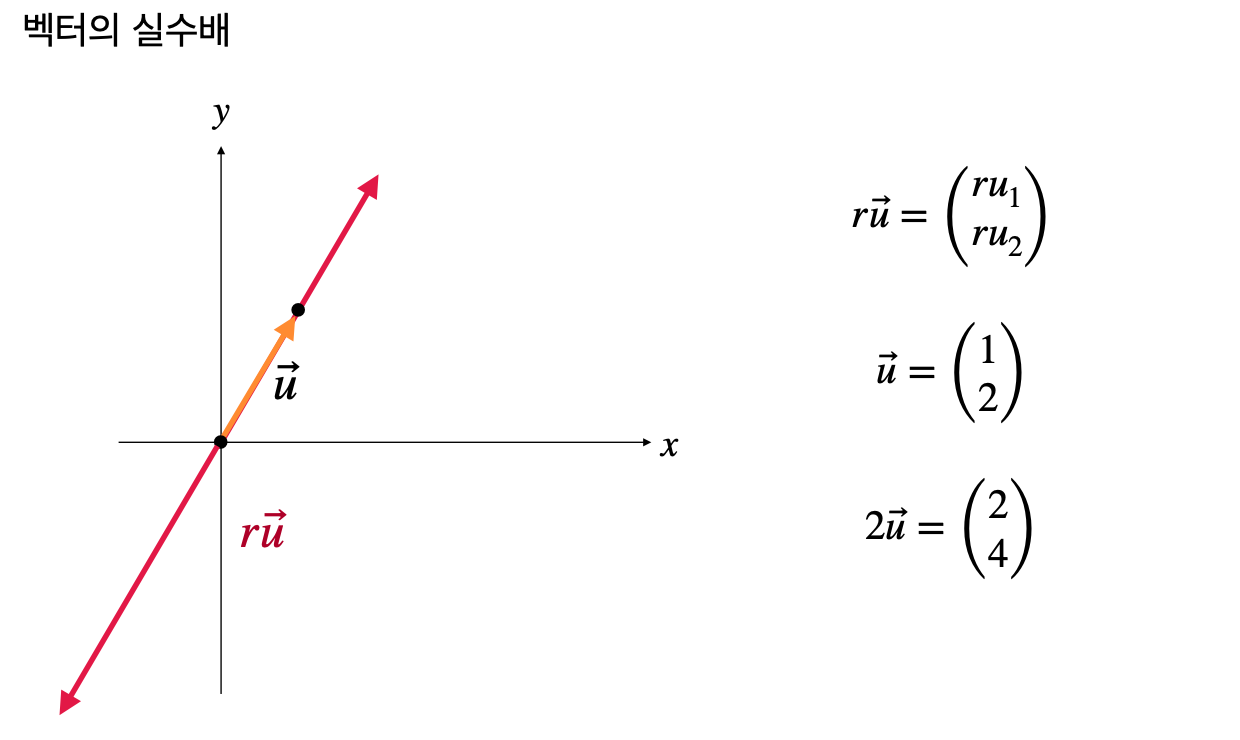
실수배는 벡터의 크기를 실수만큼 조절하는 연산이다.

 

Vector Spaces and Subspaces

 

벡터공간은 벡터 연산이 닫혀 있고, 덧셈과 스칼라곱에 대해 결합법칙과 분배법칙이 성립하는 벡터의 집합이다. 

 

부분공간은 벡터공간의 조건을 만족하는 벡터들의 집합으로, 원래의 벡터공간 내에 완전히 포함된다.

 

위 그림에서 색칠된 영역은 정의를 만족하지 못하기 때문에 부분공간이 아니다.

 

Vector Spaces and ML/DL

 

선형대수는 데이터의 차원을 다루고 변환하는 강력한 도구로, 특히 머신러닝과 데이터 과학에서 중요한 역할을 한다.

 

벡터와 벡터공간은 데이터의 구조를 이해하고, 머신러닝 모델을 설계하는 데 기본적인 빌딩 블록으로 작용한다.

 

데이터는 종종 벡터 형태로 표현되기 때문이며,

 

이미지, 텍스트, 음성 등 다양한 데이터 형태를 수치 벡터로 변환하여 처리할 수 있다.

 

따라서 벡터 공간의 개념은 데이터의 차원과 구조를 이해하는 데 도움이 된다.

 

Conclusion

 

벡터공간은 수학의 여러 분야와 과학, 공학의 다양한 응용에서 근본적인 역할을 한다.

 

이 글에서는 벡터공간의 개념을 탐구하고, ML/DL에서의 효용성에 대해 정리해 보았다.

 

미래의 나에게 도움이 되었으면 좋겠다.