[선형대수학]행렬의 랭크와 그 응용

목차

 

[선형대수학]머신러닝과 딥 러닝의 핵심, 선형대수학의 역할과 중요성

[선형대수학]부분행렬과 분할행렬: 공통점과 차이점, ML/DL에의 응용

[선형대수학]역행렬과 행렬식의 성질, ML/DL과의 관계

[선형대수학]행렬의 해와 감소된 행 계단형(Reduced Row Echelon Form, RREF)

[선형대수학]벡터 공간(Vector Spaces)

[선형대수학]벡터 공간과 일차 독립

[선형대수학]벡터 공간과 기저, 차원 그리고 ML/DL

[선형대수학]차원의 저주: 데이터 분석의 걸림돌

[선형대수학]행렬의 랭크와 그 응용

[선형대수학]벡터의 내적과 그 응용

[선형대수학]정규직교 기저와 그람-슈미트 프로세스

[선형대수학]최소 제곱해

[선형대수학]선형변환과 고윳값의 이해: 머신러닝/딥러닝에서의 응용

[선형대수학]벡터 공간의 대각화와 그 응용 - 유사 행렬 및 머신러닝에서의 중요성

[선형대수학]특이값 분해(SVD): 기본부터 머신러닝/딥러닝까지의 응용

[선형대수학]특이값 분해와 고윳값: 공통점과 차이점

[선형대수학]실 이차 형식과 양의 정부호 행렬: 머신러닝/딥러닝에의 응용

[선형대수학]주성분 분석(Principal Component Analysis, PCA)

[선형대수학]Factorization Machines

 

Introduction

 

행렬의 랭크는 선형 대수학에서 중추적인 개념이며, 데이터의 구조와 차원을 이해하는 데 필수적이다. 

 

랭크는 행렬이 가지는 독립적인 행(또는 열)의 최대 개수를 나타내며, 이는 해공간과 영공간의 차원을 결정한다. 

 

이 글에서는 행공간과 열공간의 정의, 행렬이 row equivalent인 경우 두 행렬의 행공간이 같다는 사실, 

 

랭크와 영공간, 해공간의 기저에 대해 자세히 탐구하고, 

 

이를 머신러닝과 딥러닝, 특히 Gradient Projection Method에 어떻게 적용되는지 살펴본다.

 

Row Space and Column Space

 

행렬 A의 행공간은 A의 행 벡터들에 의해 생성된 벡터 공간이며, 이는 $\mathbb{R}^n$의 부분공간이다.

 

열공간도 마찬가지로 A의 열 벡터들이 생성하는 공간으로, $\mathbb{R}^m$의 부분공간이다. 

 

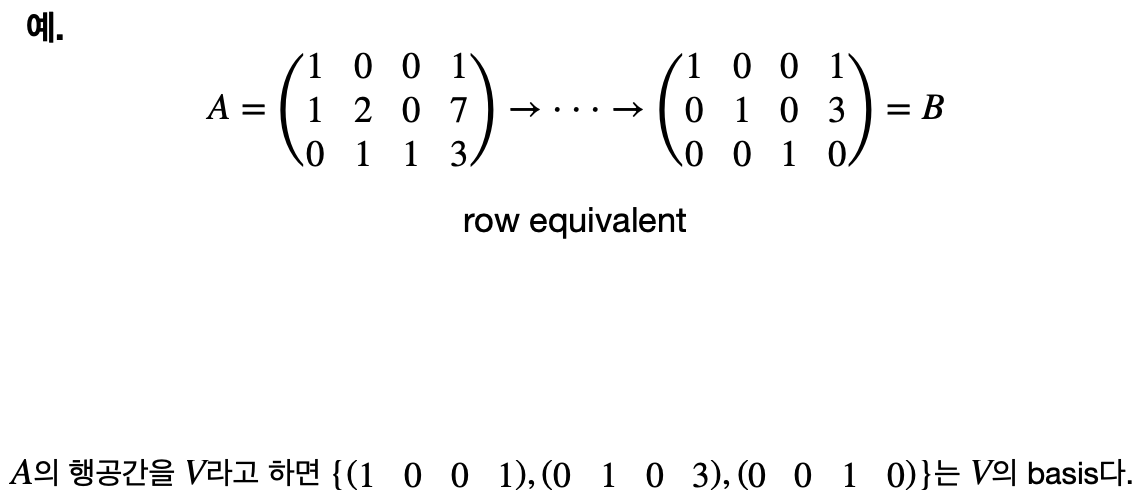
행렬이 row equivalent라면, 이들은 같은 행공간을 가지며, 

 

이는 두 행렬이 동일한 선형 변환을 나타낸다는 의미이다.

 

 

Rank

 

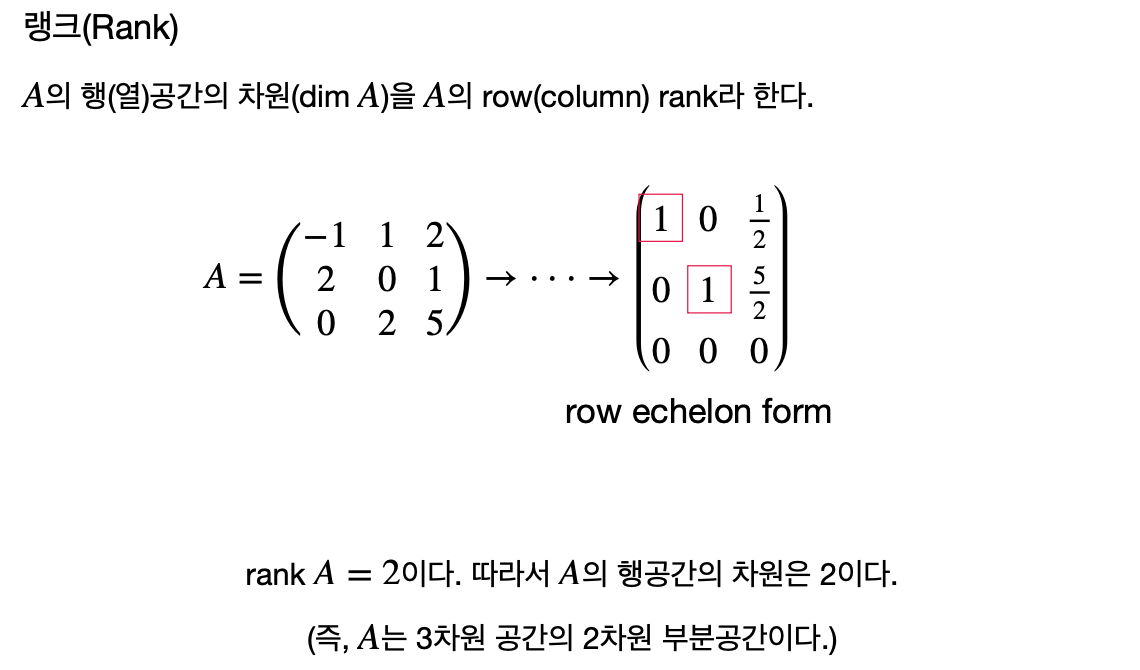
랭크는 행렬을 RREF로 변환했을 때, 비제로 행(row)의 수와 동일하다. 

 

예를 들어, 행렬 A가 echelon form으로 변환된 후 비제로 행이 k개라면, rank A = k이다. 

 

랭크는 행렬이 얼마나 '정보'를 많이 담고 있는지를 나타내며, 

 

랭크가 전체 행 또는 열의 수와 같다면, 행렬은 nonsingular하다고 한다.

 

Null Space and Solution Space

 

영공간(null space)은 선형 시스템 Ax = 0의 모든 해를 포함하는 벡터 공간으로, 

 

이는 시스템에서 자유 변수가 가질 수 있는 모든 값의 집합을 나타낸다. 

 

간단히 말해, 영공간의 기저는 주어진 행렬의 선형 변환에 의해 원점으로 매핑되는 모든 벡터들을 찾는 과정이다. 

 

해공간(solution space)은 비영구방정식 Ax = b의 해를 포함하며, 

 

이는 영공간과는 다르게 특정한 b에 대응하는 해의 집합을 의미한다. 

 

영공간의 차원인 nullity는 전체 변수의 수에서 랭크를 뺀 값으로 계산되며, 이는 시스템의 자유도를 나타낸다.

 

 

ML/DL

 

머신러닝과 딥러닝에서 랭크는 특성 행렬의 정보량을 나타내며,  이는 모델의 학습 능력에 직접적인 영향을 미친다. 

 

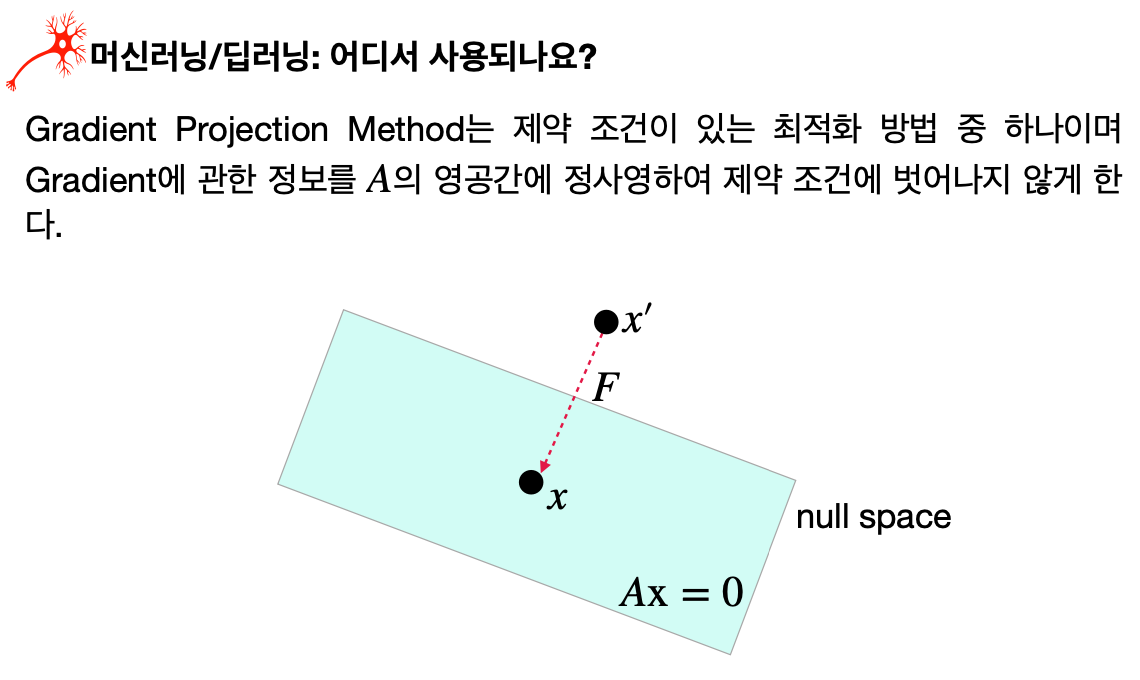
Gradient Projection Method는 제약이 있는 최적화 문제에서 영공간을 이용하여 그래디언트의 방향을 조절하고, 

 

최적의 해로의 이동 경로를 찾는데 사용된다. 

 

이 방법은 특히 제약 조건 하에서 데이터의 기저를 찾거나, 차원 축소 등의 문제에 유용하게 적용된다. 

 

높은 랭크는 복잡한 데이터 구조를 가진 모델을 의미하지만, 모델이 과적합되지 않도록 적절한 정규화와 함께 적용되어야 한다.