[선형대수학]특이값 분해(SVD): 기본부터 머신러닝/딥러닝까지의 응용

목차

 

[선형대수학]머신러닝과 딥 러닝의 핵심, 선형대수학의 역할과 중요성

[선형대수학]부분행렬과 분할행렬: 공통점과 차이점, ML/DL에의 응용

[선형대수학]역행렬과 행렬식의 성질, ML/DL과의 관계

[선형대수학]행렬의 해와 감소된 행 계단형(Reduced Row Echelon Form, RREF)

[선형대수학]벡터 공간(Vector Spaces)

[선형대수학]벡터 공간과 일차 독립

[선형대수학]벡터 공간과 기저, 차원 그리고 ML/DL

[선형대수학]차원의 저주: 데이터 분석의 걸림돌

[선형대수학]행렬의 랭크와 그 응용

[선형대수학]벡터의 내적과 그 응용

[선형대수학]정규직교 기저와 그람-슈미트 프로세스

[선형대수학]최소 제곱해

[선형대수학]선형변환과 고윳값의 이해: 머신러닝/딥러닝에서의 응용

[선형대수학]벡터 공간의 대각화와 그 응용 - 유사 행렬 및 머신러닝에서의 중요성

[선형대수학]특이값 분해(SVD): 기본부터 머신러닝/딥러닝까지의 응용

[선형대수학]특이값 분해와 고윳값: 공통점과 차이점

[선형대수학]실 이차 형식과 양의 정부호 행렬: 머신러닝/딥러닝에의 응용

[선형대수학]주성분 분석(Principal Component Analysis, PCA)

[선형대수학]Factorization Machines

 

Introduction

 

특이값 분해(SVD, Singular Value Decomposition)는 행렬을 특정한 방식으로 분해하는 강력한 수학적 도구이다. 

 

이 방법은 데이터의 구조를 이해하고, 중요한 정보를 추출하는 데 매우 유용하다. 

 

이 글에서는 SVD의 기본적인 개념을 설명하고, 이를 좌/우 특이 벡터와 특이값에 적용하는 방법, 

 

그리고 이 모든 것이 머신러닝과 딥러닝 분야에 어떻게 활용될 수 있는지를 소개해 보겠다.

 

Singular Value Decomposition

 

특이값 분해란, 어떤 $m \times n$ 크기의 실수 행렬 $A$를 세 개의 행렬 $U, Σ, V^T$의 곱으로 나타내는 것을 말한다. 

 

여기서 $U$는 $m \times m$ 크기의 orthogonal 행렬, $V$는 $n \times n$ 크기의 orthogonal 행렬이며, 

 

$Σ$는 $m \times n$ 크기의 대각 행렬이다. 

 

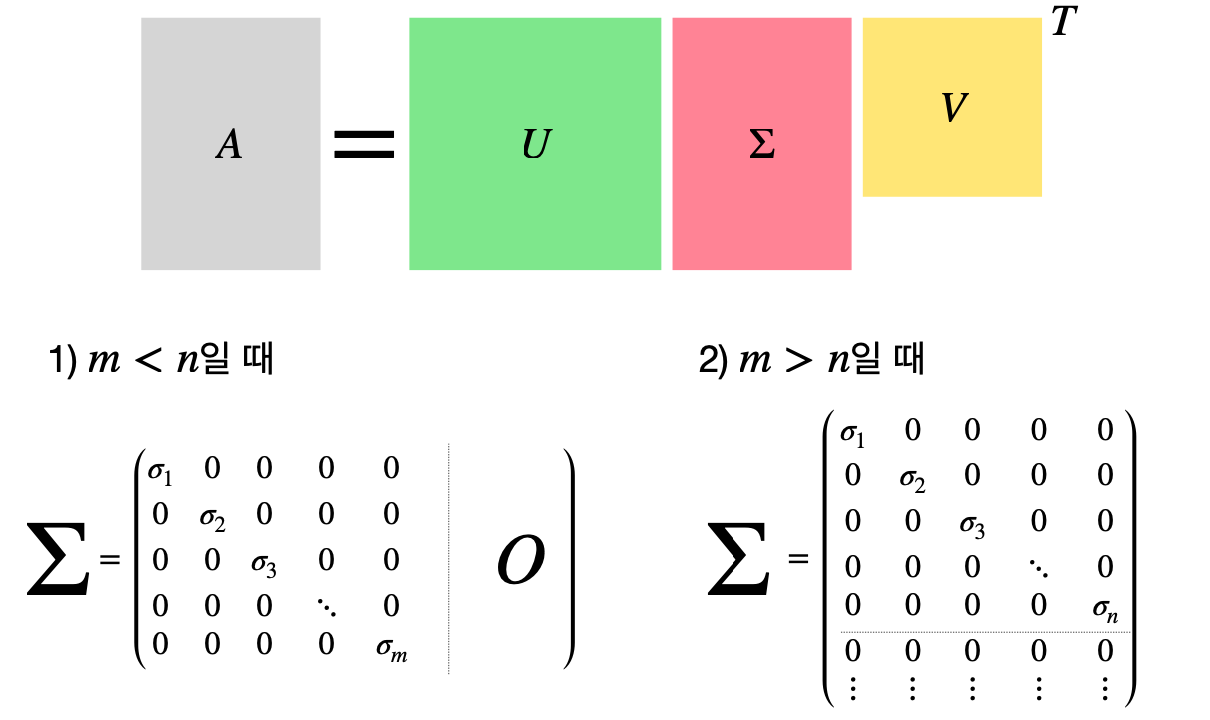
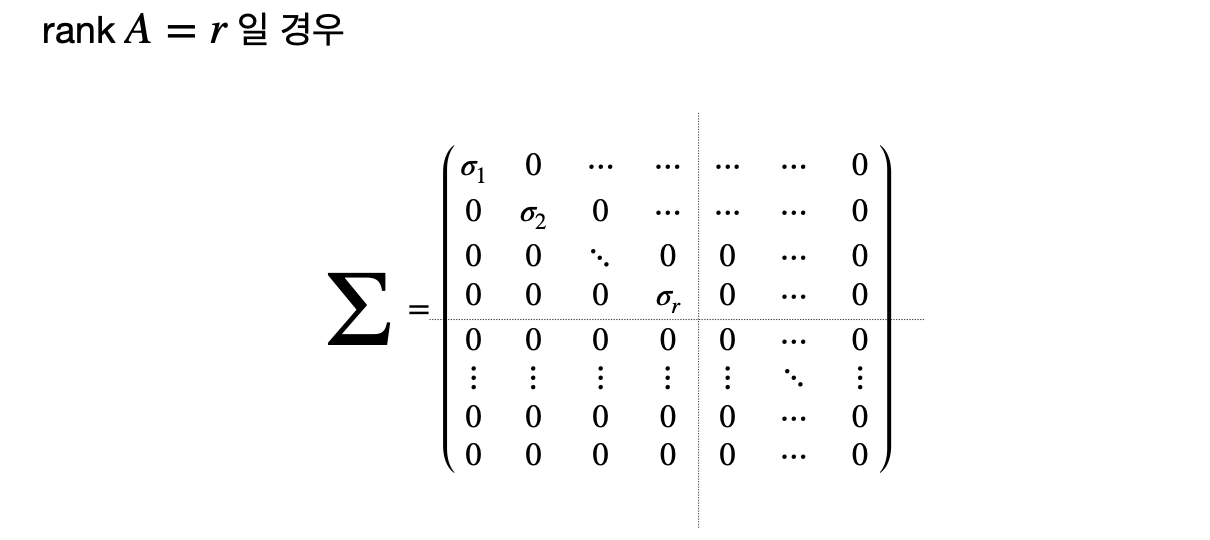
이 대각 행렬 $Σ$의 대각선 상에 위치한 값들이 바로 특이값들이며, 

 

이들은 $σ_1 ≥ σ_2 ≥… ≥ σ_g (g = min(m, n))$의 순서를 따른다. 

 

이렇게 분해된 행렬들은 $A$의 중요한 성질들을 나타내며, 데이터 분석과 처리에 매우 중요한 역할을 한다.

 

Singular Vectors and Singular Values

 

특이값 분해에서 $U$의 열 벡터들은 $A$의 '좌 특이 벡터', $V$의 열 벡터들은 $A$의 '우 특이 벡터'라고 불린다. 

 

이들은 $A$의 데이터 구조를 나타내는 데 중요한 역할을 한다. 

 

$Σ$의 대각선에 위치한 값들, 즉 특이값들은 원래 행렬 $A$의 데이터가 얼마나 '퍼져 있는지'를 나타내는 지표로 사용된다. 

 

높은 특이값은 데이터의 중요한 부분을, 낮은 특이값은 덜 중요한 부분을 나타내며, 

 

이를 통해 데이터의 중요한 특성을 파악하고 압축할 수 있다.

 

Properties of Singular Value Decomposition

 

특이값 분해는 $A$의 크기와 상관없이 항상 가능하며, $A$의 각 특이값은 항상 $0$ 이상의 값이다.

 

$AA^T = UΛ_uUT, AT A= VΛ_vVT$로 나타낼 수 있으며,

 

$ΣΣ^T = Λ_u, Σ^TΣ = Λ_v$라고 할 때 각 $σ_i$는 $\sqrt λ_i$와 동일하다. 

 

이 성질은 데이터의 분산과 밀접하게 연관되어 있으며, 이를 통해 데이터의 중요도를 평가하는 데 중요한 정보를 제공한다.

 

ML/DL

 

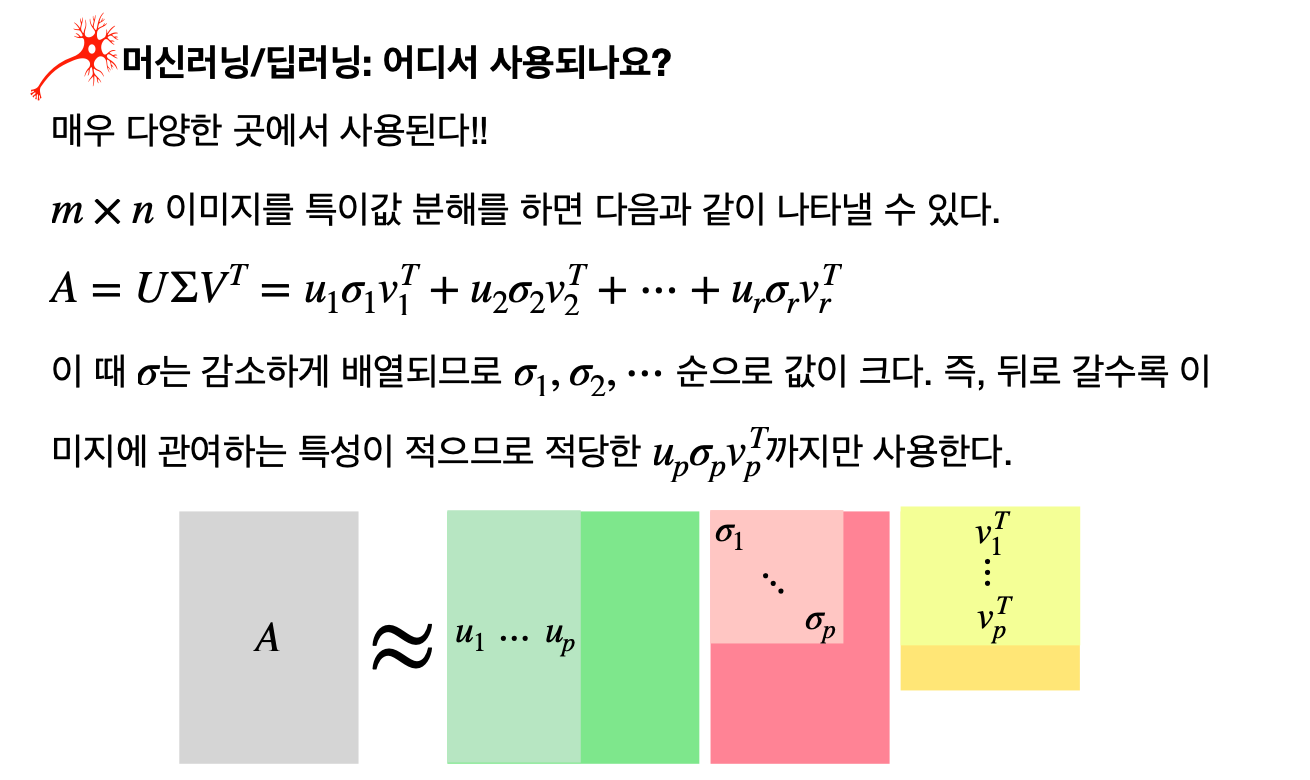
SVD는 머신러닝과 딥러닝에서 다양하게 활용된다. 

 

예를 들어, 이미지 처리에서는 이미지를 특이값 분해하여 중요한 정보만을 추출하고 나머지는 생략함으로써 

 

데이터를 압축하고 잡음을 제거할 수 있다. 

 

또한, 자연어 처리에서는 단어-문맥 행렬에 SVD를 적용하여 단어의 의미를 추출하는 데 사용된다. 

 

추천 시스템에서도 사용자와 아이템 간의 상호작용을 행렬로 나타내고 이를 분해함으로써 

 

사용자의 취향을 예측하는 데 중요한 역할을 한다.