[선형대수학]역행렬과 행렬식의 성질, ML/DL과의 관계

목차

 

[선형대수학]머신러닝과 딥 러닝의 핵심, 선형대수학의 역할과 중요성

[선형대수학]부분행렬과 분할행렬: 공통점과 차이점, ML/DL에의 응용

[선형대수학]역행렬과 행렬식의 성질, ML/DL과의 관계

[선형대수학]행렬의 해와 감소된 행 계단형(Reduced Row Echelon Form, RREF)

[선형대수학]벡터 공간(Vector Spaces)

[선형대수학]벡터 공간과 일차 독립

[선형대수학]벡터 공간과 기저, 차원 그리고 ML/DL

[선형대수학]차원의 저주: 데이터 분석의 걸림돌

[선형대수학]행렬의 랭크와 그 응용

[선형대수학]벡터의 내적과 그 응용

[선형대수학]정규직교 기저와 그람-슈미트 프로세스

[선형대수학]최소 제곱해

[선형대수학]선형변환과 고윳값의 이해: 머신러닝/딥러닝에서의 응용

[선형대수학]벡터 공간의 대각화와 그 응용 - 유사 행렬 및 머신러닝에서의 중요성

[선형대수학]특이값 분해(SVD): 기본부터 머신러닝/딥러닝까지의 응용

[선형대수학]특이값 분해와 고윳값: 공통점과 차이점

[선형대수학]실 이차 형식과 양의 정부호 행렬: 머신러닝/딥러닝에의 응용

[선형대수학]주성분 분석(Principal Component Analysis, PCA)

[선형대수학]Factorization Machines

 

Introduction

 

역행렬은 선형 대수학에서 기본적이면서 중대한 개념이다. 

 

주어진 정사각 행렬 A에 대하여, 곱셈에 대한 역원인 B, 즉 AB=BA=I를 만족하는 B를 A의 역행렬이라 한다. 

 

이 글에서는 역행렬과 행렬식의 성질에 대해 상세히 논의하고,

 

이들이 머신러닝과 딥러닝에 어떠한 영향을 미치는지 탐구하고자 한다.

 

Properties of Inverse Matrices

 

역행렬은 다음과 같은 성질을 가진다:

 

• 행렬 A가 가역행렬이기 위해서는 det(A) ≠ 0이어야 한다. 이 조건이 만족할 때, A에 대한 역행렬이 존재하며,
  A는 가역행렬(Invertible Matrices), 혹은 비특이행렬(Nonsingular Matrices)이라고 할 수 있다.
• 역행렬은 고유하며, 어떤 행렬에 대해 둘 이상의 역행렬이 존재할 수 없다.
• 역행렬의 역행렬은 원래의 행렬이다, 즉 $(A^{-1})^{-1}=A$.
• 두 행렬의 곱의 역행렬은 각 행렬의 역행렬의 곱과 같고 순서가 반대이다, 즉 $(AB)^{-1}=B^{-1}A^{-1}$.

 

 

Properties of Determinants

 

 

행렬식은 다음과 같은 중요한 성질을 갖는다:

 

• 두 열(또는 행)이 동일하거나 모든 성분이 0인 열(또는 행)이 있을 경우 행렬식은 0이다.
• 행렬에서 한 행에 다른 행을 상수배하여 더하거나, 행의 위치를 바꾸는 등의 기본 행 연산은 행렬식에 특정한 영향을 미친다.
• 상삼각행렬 또는 하삼각행렬의 행렬식은 대각선상의 원소들의 곱이다.
• 두 행렬의 곱의 행렬식은 각각의 행렬식의 곱이다.
• 역행렬의 행렬식은 원 행렬의 행렬식의 역수와 같다.

 

 

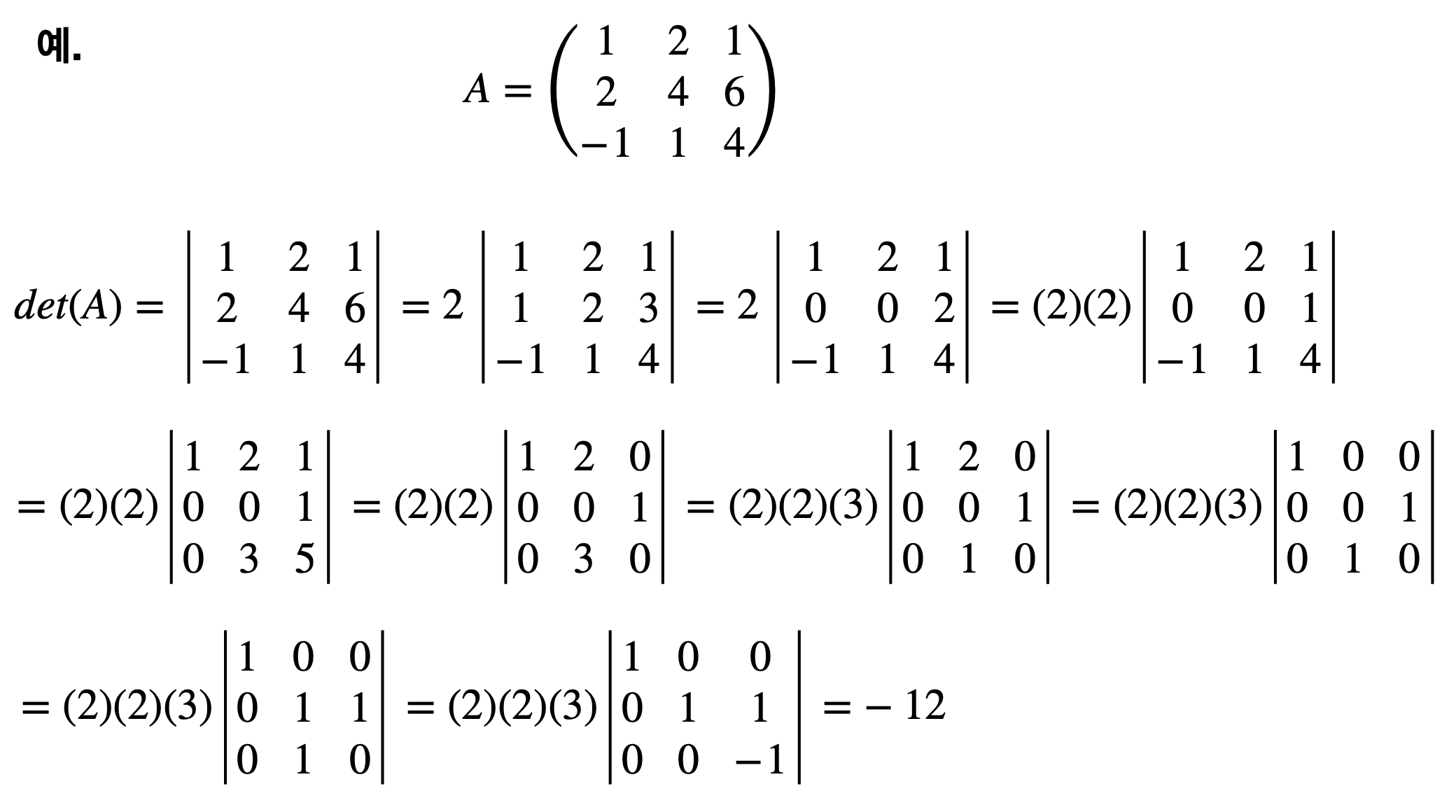
Inverse Matrices, Determinants, and ML/DL

 

역행렬과 행렬식은 머신러닝과 딥러닝에서 중요한 역할을 한다. 

 

예를 들어, 행렬식은 데이터의 독립성을 측정하는데 사용되며, 역행렬은 최적화 문제에서 해를 찾는 데 필수적이다. 

 

또한, 신경망의 가중치를 업데이트하는 과정에서 역전파 알고리즘을 사용할 때 역행렬이 필요할 수 있다. 

 

이러한 알고리즘의 효율성은 종종 행렬식의 계산 능력에 의존한다.

 

Conclusion

 

역행렬과 행렬식은 선형 대수학의 근본적인 개념으로, 

 

머신러닝과 딥러닝의 이론과 실제 적용에 있어 기본적인 토대를 제공한다. 

 

이들의 성질을 이해하고 활용하는 것은 복잡한 데이터 구조를 해석하고, 학습 알고리즘을 개발하는 데 있어 필수적이다.