[선형대수학]벡터 공간의 대각화와 그 응용 - 유사 행렬 및 머신러닝에서의 중요성

목차

 

[선형대수학]머신러닝과 딥 러닝의 핵심, 선형대수학의 역할과 중요성

[선형대수학]부분행렬과 분할행렬: 공통점과 차이점, ML/DL에의 응용

[선형대수학]역행렬과 행렬식의 성질, ML/DL과의 관계

[선형대수학]행렬의 해와 감소된 행 계단형(Reduced Row Echelon Form, RREF)

[선형대수학]벡터 공간(Vector Spaces)

[선형대수학]벡터 공간과 일차 독립

[선형대수학]벡터 공간과 기저, 차원 그리고 ML/DL

[선형대수학]차원의 저주: 데이터 분석의 걸림돌

[선형대수학]행렬의 랭크와 그 응용

[선형대수학]벡터의 내적과 그 응용

[선형대수학]정규직교 기저와 그람-슈미트 프로세스

[선형대수학]최소 제곱해

[선형대수학]선형변환과 고윳값의 이해: 머신러닝/딥러닝에서의 응용

[선형대수학]벡터 공간의 대각화와 그 응용 - 유사 행렬 및 머신러닝에서의 중요성

[선형대수학]특이값 분해(SVD): 기본부터 머신러닝/딥러닝까지의 응용

[선형대수학]특이값 분해와 고윳값: 공통점과 차이점

[선형대수학]실 이차 형식과 양의 정부호 행렬: 머신러닝/딥러닝에의 응용

[선형대수학]주성분 분석(Principal Component Analysis, PCA)

[선형대수학]Factorization Machines

 

Introduction

 

벡터 공간에서의 대각화는 선형대수와 머신러닝의 핵심을 이루는 중요한 개념이다. 

 

복잡한 선형 변환을 간단한 형태로 나타내는 것이 가능하며, 이를 통해 데이터의 구조와 특성을 더 명확히 이해할 수 있다. 

 

이 글에서는 누구나 쉽게 이해할 수 있도록, 벡터 공간의 대각화에 대해 자세히 설명하고, 

 

특히 유사 행렬과 대각화의 중요성을 중점적으로 다루겠다. 

 

또한, 이러한 수학적 개념이 어떻게 머신러닝과 딥러닝에 적용될 수 있는지도 함께 살펴보겠다.

 

Similarity

 

유사성이란 두 행렬이 특정한 관계를 가지고 있는 것을 의미한다. 

 

구체적으로, 두 행렬 A와 B가 있을 때, 어떤 nonsingular 행렬 P가 존재하여 $B = P^{−1}AP$를 만족한다면, 

 

우리는 'A는 B와 유사하다'라고 한다. 

 

이 개념은 두 행렬이 기본적으로 같은 선형 변환을 다른 기저에서 표현하고 있다는 것을 의미한다. 

 

유사한 행렬들은 고유값이 동일하다는 중요한 성질을 가지고 있으며, 이는 대각화 과정에서 핵심적인 역할을 한다.

 

Diagonalization

 

대각화는 행렬을 대각 행렬, 즉 대부분의 원소가 0이고 대각선 위에만 값이 있는 형태로 변환하는 과정이다. 

 

이 과정을 통해 행렬의 선형 변환을 더 단순하게 표현할 수 있다. 

 

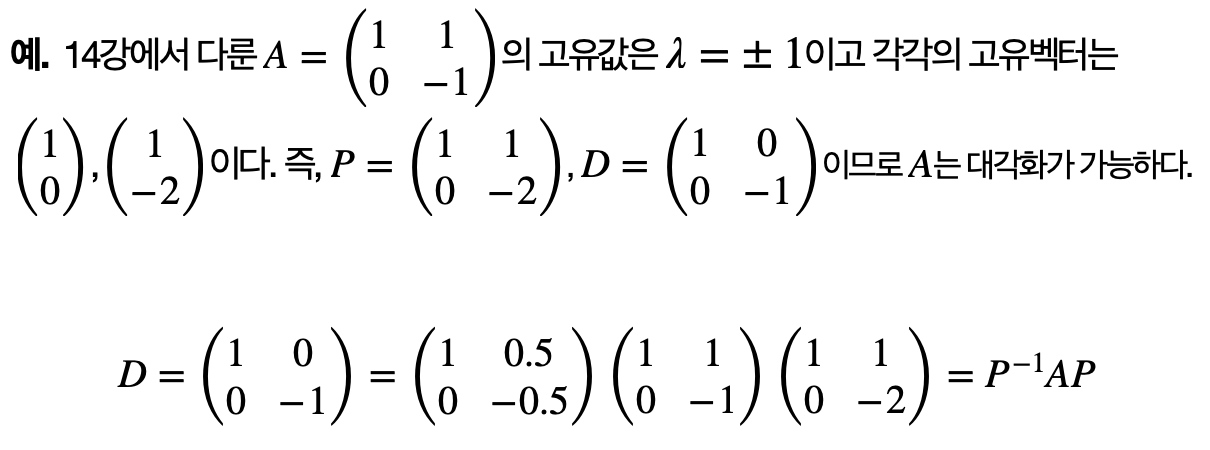
대각화가 가능한지를 판별하는 것은 중요한데, 이는 행렬이 충분한 수의 일차 독립인 고유벡터를 가지고 있는지에 달려 있다. 

 

이를 위해, 행렬의 고유값과 고유벡터를 찾는 것이 필수적이며, 이러한 과정은 선형대수학에서 매우 중요한 위치를 차지한다.

 

Diagonalization Characteristics and Orthogonal Matrices

 

대칭행렬은 고유값이 모두 실수라는 특별한 특성을 가지고 있으며, 이들의 고유 벡터는 서로 직교한다. 

 

이러한 성질은 데이터 분석과 머신러닝에서 특히 중요한데,

 

데이터의 주요 축을 찾고 이를 통해 데이터를 간소화하는 데 사용된다. 

 

직교 행렬은 자신의 전치 행렬이 자신의 역행렬과 같은 성질을 가지고 있으며, 

 

이는 각 열(또는 행)이 단위 길이를 가지고 상호 직교하는 벡터들로 구성되어 있음을 의미한다.

 

Specific Steps of Diagonalization

 

대각화를 진행하는 구체적인 단계는 다음과 같다:

1. 고윳값을 찾는다. 이는 주어진 행렬의 특성 방정식을 해결함으로써 이루어진다.
2. 각 고유값에 대응하는 일차 독립인 고유벡터를 찾는다.
3. 대칭 행렬의 경우, 직교 고유벡터를 찾거나 Gram-Schmidt 방법을 사용해 직교화한다.
4. 정규 직교 고유벡터를 계산하여 행렬을 단위 벡터들의 집합으로 변환한다.
5. 마지막으로, 대각화된 행렬을 얻기 위해 $P^{-1}AP$ 또는 $P^{T}AP$를 계산한다.

 

ML/DL

 

대각화는 머신러닝과 딥러닝에서 중요한 역할을 한다. 

 

특히, 고유값 분해나 특이값 분해 같은 기법을 통해 데이터의 차원을 축소하고, 중요한 특성을 추출하는 데 사용된다. 

 

이는 복잡한 데이터 세트를 더 잘 이해하고, 효율적으로 처리할 수 있게 해 주며, 

 

결과적으로 더 정확하고 강력한 머신러닝 모델을 구축하는 데 기여한다.

 

Conclusion

 

이 글을 통해 벡터 공간에서의 대각화, 유사 행렬의 중요성, 

 

그리고 이 개념들이 머신러닝과 딥러닝에 어떻게 응용될 수 있는지에 대해 자세히 살펴보았다. 

 

이러한 수학적 이해는 미래의 데이터 과학과 인공 지능 분야에서 중요한 역할을 할 것으로 기대된다. 

 

데이터를 더 잘 이해하고, 효과적으로 활용하는 것이 이러한 분야에서의 핵심적인 도전이자 목표이기 때문이다.